沪教版(上海)八年级下册数学 第二十二章 四边形 第3节 梯形 同步测试题(含答案)
文档属性
| 名称 | 沪教版(上海)八年级下册数学 第二十二章 四边形 第3节 梯形 同步测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 263.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 10:11:32 | ||
图片预览



文档简介
第二十二章 四边形 第3节 梯形 同步测试题
一.选择题
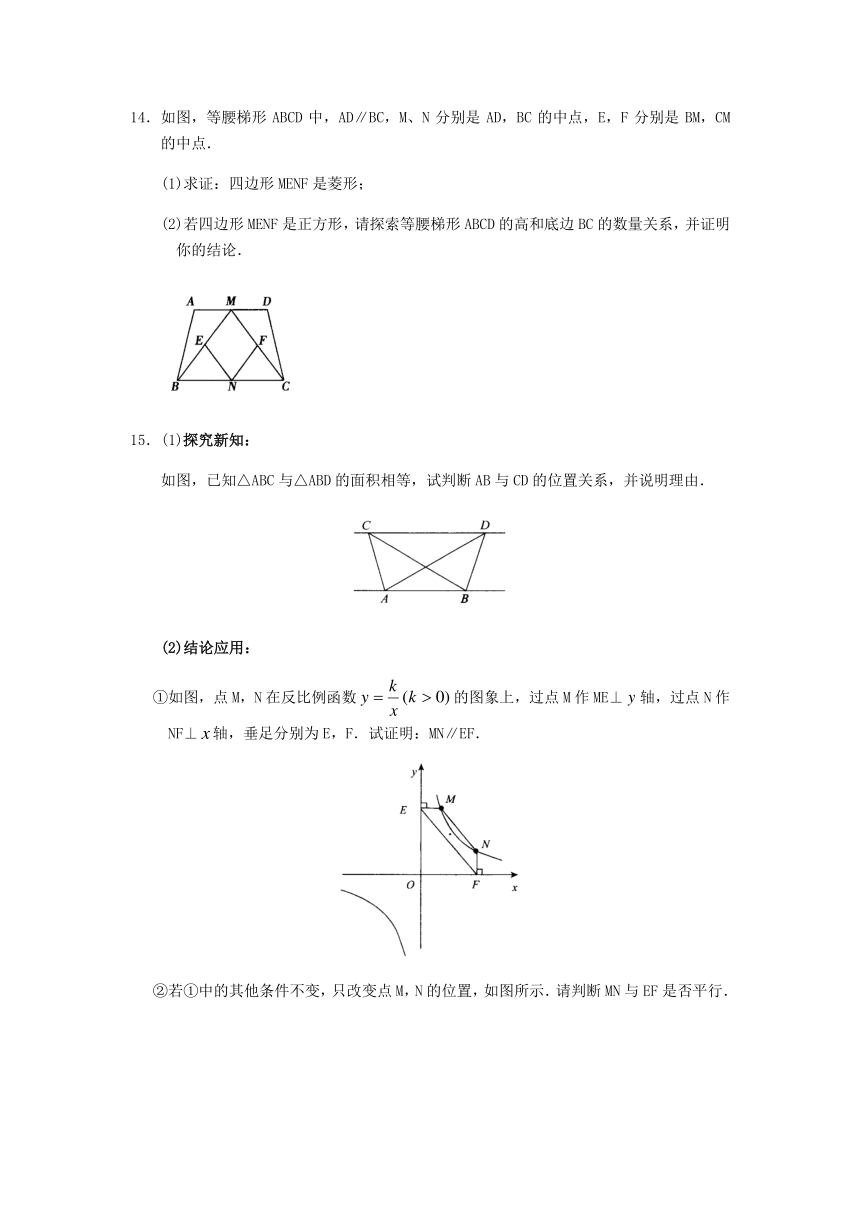
1.如图,等腰梯形ABCD中,AB∥CD,对角线AC平分∠BAD,∠B=60°,CD=2,则梯形ABCD的面积是( )
A. B.6 C. D.12
2.等腰梯形ABCD中,AB∥CD,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积是( )
A. B. C. D.
3.如图,平行四边形ABCD是用12个全等的等腰梯形镶嵌成的图形,这个图形中等腰梯形的上底长与下底长的比是( ).
A. 1∶2 B. 2∶3 C. 3∶5 D. 4∶7
4.梯形ABCD中,AD∥BC,若对角线AC⊥BD,且AC=5,BD=12,则梯形的面积等于( )
A.30 B.60c C.90 D.169c
5.如图,在梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,则下列结论:
①EF∥AD;②;③△OGH是等腰三角形;④BG=DG;⑤EG=HF.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6. 如图,在梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底的差是6,两腰的和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
二.填空题
7. 如图,已知在梯形ABCD中,AD//BC,AB=CD,且AC⊥BD,AC=6,则梯形的高为________.
8. 如图,G是△ABC的重心,=4,=________.
9. 如图,DE是△ABC的中位线,M、N分别是BD、CE的中点,MN=6,则BC=_____.
10.如图,梯形ABCD中,AD∥BC,AB=CD=AD=1,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,那么PC+PD的最小值为______.
11.在梯形ABCD中,AD∥BC,AD=5,BC=7,若E为DC的中点,射线AE交BC的延长线于F点,则BF=______.
12.如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_________.
三.解答题
13.如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
(1)求证:梯形ABCD是等腰梯形;
(2)若∠BDC=30°,AD=5,求CD的长.
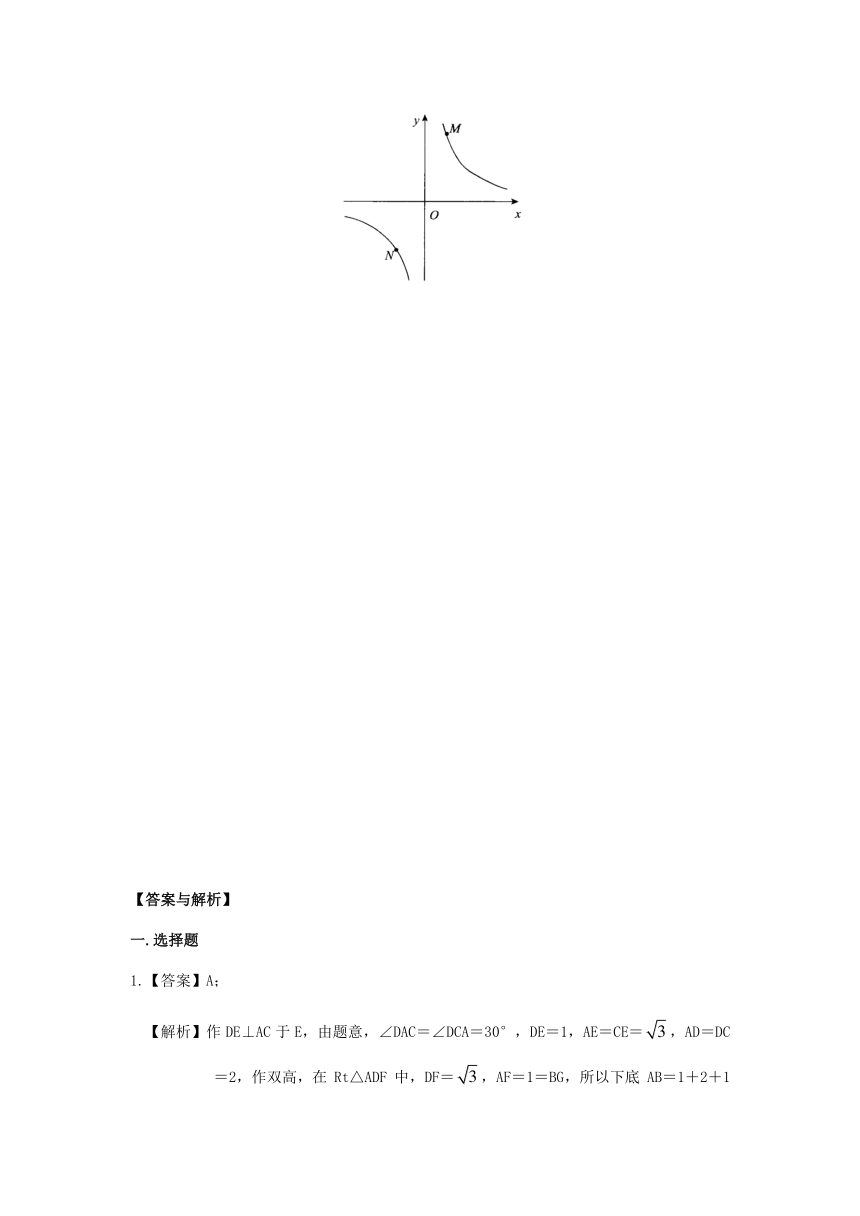
14.如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD,BC的中点,E,F分别是BM,CM的中点.
(1)求证:四边形MENF是菱形;
(2)若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,并证明你的结论.
15.(1)探究新知:
如图,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
①如图,点M,N在反比例函数的图象上,过点M作ME⊥轴,过点N作NF⊥轴,垂足分别为E,F.试证明:MN∥EF.
②若①中的其他条件不变,只改变点M,N的位置,如图所示.请判断MN与EF是否平行.
【答案与解析】
一.选择题
1.【答案】A;
【解析】作DE⊥AC于E,由题意,∠DAC=∠DCA=30°,DE=1,AE=CE=,AD=DC=2,作双高,在Rt△ADF中,DF=,AF=1=BG,所以下底AB=1+2+1=4,面积=.
2.【答案】B;
【解析】作双高,解得高=,所以面积为.
3.【答案】A;
【解析】等腰梯形的上底长等于腰长,可推算出底角=60°,上底长与下底长的比是1:2.
4.【答案】A;
【解析】平移对角线,所得三角形面积就是梯形的面积,三角形面积.
5.【答案】D;
【解析】根据梯形的中位线推出①,求出△ABD和△ACD的面积,都减去△AOD的面积,即可判断②;只有等腰梯形ABCD,才能得出∠OBC=∠OCB,再根据平行线性质即可判断③;根据三角形中位线推论可得出G、H分别为BD和AC中点,即可判断④;根据三角形的中位线得出EH=FG,即可得出EG=FH,即可判断⑤.
6.【答案】B;
【解析】连接AE,延长交CD于H,可证AB=DH,CH=两底的差,EF是△AHC的中位线,EF=两底的差,EG+FG=两腰的和,故△EFG的周长是9.
二.填空题
7.【答案】;
【解析】过D点作DE∥AC,交BC于E,作DF⊥BE于F,则∠BDE=90°,BD=DE=AC=6,所以DF=BF=EF=.
8.【答案】24;
【解析】由于G是△ABC的重心,可得AG=2GD,BD=CD,根据等高三角形的面积比等于底之比,可求出=12;同理D是BC中点,可得出=2=24.
9.【答案】8;
【解析】∵DE是△ABC的中位线,∴DE=BC,DE∥BC∵M、N分别是BD、CE的中点,∴由梯形的中位线定理得:MN=(DE+BC)=×BC=6,∴BC=8.
10.【答案】;
【解析】连接BD,过D作DE⊥BC,在Rt△DCE中,CE=,DE=,BE=1+=,所以BD=,因为B是C关于MN的对称点,所以BD就是PC+PD的最小值.
11.【答案】12;
【解析】△ADE≌△FCE,AD=CF,所以BF=5+7=12.
12.【答案】或2或;
【解析】当AB=AE时,CF=,当AE=BE时,CF=,当AB=AE时,CF=2.
三.解答题
13.【解析】
解:(1)∵AE∥BD,
∴∠E=∠BDC.
∵DB平分∠ADC,
∴∠ADC=2∠BDC.
∵∠C=2∠E,
∴∠ADC=∠BCD.
∴梯形ABCD是等腰梯形(同一底上的两个角相等的梯形是等腰梯形).
(2)由第(1)问,得∠C=2∠E=2∠BDC=60°,且BC=AD=5,
∵在△BCD中,∠C=60°,∠BDC=30°,
∴∠DBC=90°.
∴DC=2BC=10.
14.【解析】
(1)证明:∵四边形ABCD为等腰梯形,
∴AB=CD,∠A=∠D.
∵M为AD的中点,
∴AM=DM.
∴△ABM≌△DCM.
∴BM=CM.
∵E、F、N分别是MB、CM、BC的中点,
∴EN、FN分别为△BMC的中位线,
∴EN=MC,FN=MB,且ME=BE=MB,MF=FC=MC.
∴EN=FN=FM=EM.
∴四边形ENFM是菱形.
(2)解:结论:等腰梯形ABCD的高是底边BC的一半.
理由:连接MN,
∵BM=CM,BN=CN,
∴MN⊥BC.
∵AD∥BC,
∴MN⊥AD.
∴MN是梯形ABCD的高.
又∵四边形MENF是正方形,
∴△BMC为直角三角形.
又∵N是BC的中点,
∴MN=BC.
15.【解析】
(1)证明:分别过点C,D作CG⊥AB,DH⊥AB.垂足为G,H,如图1,则∠CGA=
∠DHB=90°.
图1
∴CG∥DH
∵△ABC与△ABD的面积相等
∴CG=DH
∴四边形CGHD为平行四边形
∴AB∥CD.
(2)①证明:连结MF,NE,如图2,设点M的坐标为(),点N的坐标为(),
∵点M,N在反比例函数的图象上,
图2
∴.
∵ME⊥轴,NF⊥轴,
∴OE=,OF=.
∴=;=.
∴.
由(1)中的结论可知:MN∥EF.
②如图3所示,MN∥EF.
图3
