北师大版七年级数学下册5.3 简单的轴对称图形(有关等腰三角形的问题)
文档属性
| 名称 | 北师大版七年级数学下册5.3 简单的轴对称图形(有关等腰三角形的问题) |  | |
| 格式 | zip | ||
| 文件大小 | 170.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 23:25:20 | ||
图片预览




文档简介
等腰三角形中易漏解或多解得问题
求长度时忽略三边关系
1.已知等腰三角形两边长为3和7,则周长为( )
A.13 B.17 C.13或17 D.11
2.已知一个等腰三角形的三边长分别为2x﹣1、x+1、3x﹣2,求这个等腰三角形的周长.
(1)完成部分解题过程,在以下解答过程的空白处填上适当的内容.
解:①当2x﹣1=x+1时,解x= ,此时 构成三角形(填“能”或“不能”).
②当2x﹣1=3x﹣2时,解x= ,此时 构成三角形(填“能”或“不能”).
(2)请你根据(1)中两种情况的分类讨论,完成第三种情况的分析,若能构成等腰三角形,求出这个三角形的周长.
3.已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分,求这个等腰三角形的底边长和腰长.
当腰和底不明求角度时没有分类讨论
4.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
5.有一个三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则∠C的度数 。
6.等腰三角形一腰上的高与另一腰的夹角为35°,求这个三角形的各个内角的度数.
答案:
B.
2.解:(1)①当2x﹣1=x+1时,解x=2,此时3,3,4,能构成三角形.
②当2x﹣1=3x﹣2时,解x=1,此时1,2,1不能构成三角形.
故答案为2,能,1,不能;
(2)③当x+1=3x﹣2,解得x=,此时2,,能构成三角形,周长为7.
3.解:设三角形的腰为x,如图:
△ABC是等腰三角形,AB=AC,BD是AC边上的中线,
则有AB+AD=9或AB+AD=15,分下面两种情况解.
(1)x+x=9,∴x=6,∵三角形的周长为9+15=24cm, ∴三边长分别为6,6,12
∵6+6=12,不符合三角形的三边关系 ∴舍去;
(2)x+x=15 ∴x=10 ∵三角形的周长为24cm ∴三边长分别为10,10,4.
综上可知:这个等腰三角形的底边长为4cm,腰长为10cm.
4. C.
5.40°或25°或10°
6.解:①此等腰三角形为钝角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°, ∴此三角形的顶角=90°+35°=125°,
∴等腰三角形的各角的度数为125°,27.5°,27.5°;
②此等腰三角形为锐角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°,
∴此三角形的顶角=90°﹣35°=55°,
所以等腰三角形的各角的度数为55°,62.5°,62.5°.
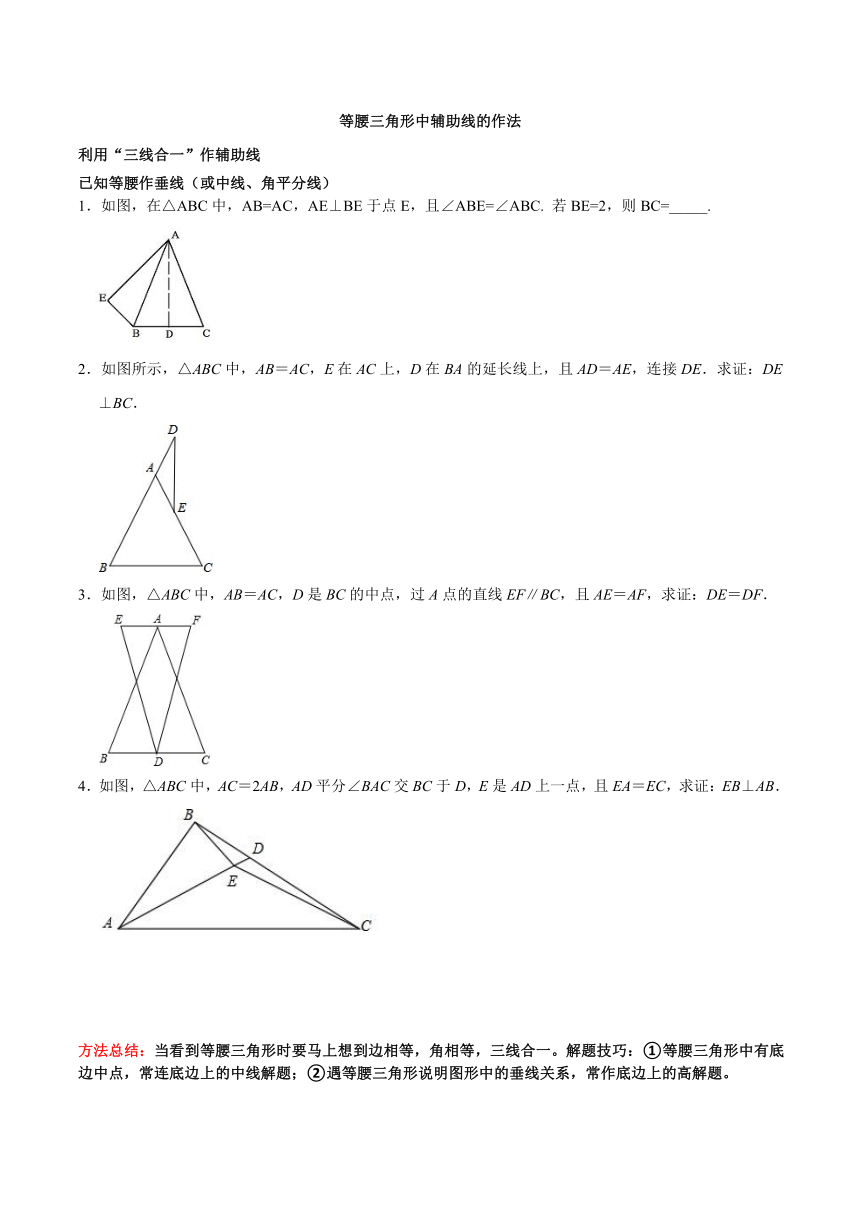
等腰三角形中辅助线的作法
利用“三线合一”作辅助线
已知等腰作垂线(或中线、角平分线)
1.如图,在△ABC中,AB=AC,AE⊥BE于点E,且∠ABE=∠ABC. 若BE=2,则BC=_____.
2.如图所示,△ABC中,AB=AC,E在AC上,D在BA的延长线上,且AD=AE,连接DE.求证:DE⊥BC.
3.如图,△ABC中,AB=AC,D是BC的中点,过A点的直线EF∥BC,且AE=AF,求证:DE=DF.
4.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.
方法总结:当看到等腰三角形时要马上想到边相等,角相等,三线合一。解题技巧:①等腰三角形中有底边中点,常连底边上的中线解题;②遇等腰三角形说明图形中的垂线关系,常作底边上的高解题。
巧用“角平分线+垂线合一”构造等腰三角形(拓展)
拓展点拨:如图,△ABC中,AD平分∠BAC,AD⊥BC,由“ASA”易得△ABD≌△ACD ,从而得AB=AC,BD=CD。即一边上的高与这边所对的角平分线重合,易得这个三角形是等腰三角形。
5.已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.
求证:BD=2CE.
6.如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
(1)求证:∠BCN=∠CAE;
(2)求证:AE=CN+EN(请用多种方法证明)
7.已知,如图AB=AC,∠A=108°,BD平分∠ABC交AC于D,求证:BC=AB+CD.
方法总结:用截长补短法说明线段的和差关系:截长法:在长边上截取一条与某一条短边相等的线段,再说明剩下的线段与另一短边相等;补短法:延长短边得到与长边相等的线段,再说明延长线与另一短边相等。
答案:
4
2、证明:如图,过A作AM⊥BC于M,
∵AB=AC,∴∠BAC=2∠BAM,
∵AD=AE, ∴∠D=∠AED, ∴∠BAC=∠D+∠AED=2∠D, ∴∠BAC=2∠BAM=2∠D,
∴∠BAM=∠D, ∴DE∥AM,
∵AM⊥BC, ∴DE⊥BC.
3、证明:如图,连接AD.
∵△ABC中,AB=AC,D是BC的中点,∴AD⊥BC,
∵EF∥BC,∴AD⊥EF,又AE=AF,∴AD垂直平分EF,∴DE=DF.
4、证明:作EF⊥AC于F,
∵EA=EC,∴AF=FC=AC,∵AC=2AB,∴AF=AB,
∵AD平分∠BAC交BC于D,∴∠BAD=∠CAD,
在△BAE和△FAE中,∴△ABE≌△AFE(SAS),∴∠ABE=∠AFE=90°.
∴EB⊥AB.
5、证明:延长BA和CE交于点M,
∵CE⊥BD,∴∠BEC=∠BEM=90°,∵BD平分∠ABC,∴∠MBE=∠CBE,
在△BME和△BCE中,∴△BME≌△BCE(ASA),∴EM=EC=MC,
∵△ABC是等腰直角三角形,∴∠BAC=∠MAC=90°,BA=AC,∴∠ABD+∠BDA=90°,
∵∠BEC=90°,∴∠ACM+∠CBE=90°,
∵∠BDA=∠EDC,∴∠ABE=∠ACM,
在△ABD和△ACM中,∴△ABD≌△ACM(ASA),∴DB=MC,∴BD=2CE.
6、证明:(1)∵∠CAB=∠CBA=45°,∴∠ACB=90°,
∵CN⊥AE,∴∠COE=90°,∴∠CEA+∠1=90°,∠CEA+∠2=90°,∴∠BCN=∠CAE;
(2)法一:如图1,延长CN至F,使CF=AE,连接BF,
在△CAE和△BCF中,∴△CAE≌△BCF(SAS),∴∠ACE=∠CBF=90°,CE=BF,
∵∠CBA=45°,∴∠FBN=45°=∠EBN,∵E为BC中点,∴CE=BE=BF,
在△EBN和△FBN中,,∴△EBN≌△FBN(SAS),∴NE=NF,∴AE=CN+EN.
法二:如图2,在AE上截取AF=CN,
在△ACF和△CBN中,,∴△ACF≌△CBN,∴CF=BN,∠ACF=∠B=45°,
∴∠ECF=45°=∠B,
在△BEN和△CEF中,,∴△BEN≌△CEF,∴EN=EF,∴AE=AF+EF=CN+EN.
7、证明:在线段BC上截取BE=BA,连接DE.
∵BD平分∠ABC,∴∠ABD=∠EBD=∠ABC.
在△ABD和△EBD中,,∴△ABD≌△EBD.(SAS)
∴∠BED=∠A=108°,∠ADB=∠EDB.
又∵AB=AC,∠A=108°,∠ACB=∠ABC=×(180°﹣108°)=36°,
∴∠ABD=∠EBD=18°.∴∠ADB=∠EDB=180°﹣18°﹣108°=54°.
∴∠CDE=180°﹣∠ADB﹣∠EDB=180°﹣54°﹣54°=72°.
∴∠DEC=180°﹣∠DEB=180°﹣108°=72°.∴∠CDE=∠DEC.∴CD=CE.
∴BC=BE+EC=AB+CD.
等腰三角形与全等、垂直平分线、角平分线的综合
一.选择题
1.如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
A.55° B.45° C.35° D.65°
2.如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是( )
A.AD=BD B.BD=CD C.∠1=∠2 D.∠B=∠C
3.如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
A.13 B.15 C.17 D.19
4.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
A.45° B.50° C.51° D.52°
5.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
6.如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.① B.② C.①② D.①②③
8.等腰△ABC纸片(AB=AC)可按图中所示方法折成一个四边形,点A与点B重合,点C与点D重合,请问原等腰△ABC中的∠B=( )度.
A.48° B.60° C.72° D.80°
二.填空题
9.如图,是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上,AD和BC的关系为 .
10.如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 .
11.如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为 ,∠A的度数为 .
12.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
13.如图,△ABC中,∠ABC与∠ACB的外角平分线交于P,PM⊥AC于M,若PM=6cm,则点P到AB的距离为 .
三.解答题
14.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
(1)已知∠A=50°,求∠CBE的度数;
(2)已知△BCE的周长为9,BC=4,求AB的长.
15.如图,BM平分∠ABC,D是BM上一点,过点D作DE⊥AB,DF⊥BC,分别交AB于点E,交BC于点F,P是BM上的另一点,连接PE,PF.
(1)若∠EDF=124°,求∠ABC的度数;
(2)求证:PE=PF.
16.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现∠A与∠NMB有什么关系,试证明之.
17.如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”.例如,在△ABC中,如果∠A=50°,∠B=100°,那么△ABC就是一个“倍角三角形”.
(1)已知倍角三角形的一个内角为150°,求这个三角形的另两个角的度数;
(2)已知倍角三角形是一个等腰三角形,求它的顶角的度数;
(3)如果第(2)小题中等腰三角形的底边长为4cm,求它的腰长.
答案:
一.选择题
1、A. 2、A. 3、B. 4、A. 5、B. 6、C. 7、D. 8、C.
二.填空题
9.AD垂直平分BC.
10.9.
11.解:∵在△ABA1中,∠B=20°,AB=A1B,∴∠A=∠BA1A===80°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,∴∠CA2A1===40°;
同理可得,∠EA3A2=20°,
故答案为:20° 80°.
12.
解:∵∠AOB=60°,OC平分∠AOB,∴∠AOC=30°,
①当E在E1时,OE=CE,
∵∠AOC=∠OCE=30°,∴∠OEC=180°﹣30°﹣30°=120°;
②当E在E2点时,OC=OE,则∠OCE=∠OEC=(180°﹣30°)=75°;
③当E在E3时,OC=CE,则∠OEC=∠AOC=30°;
故答案为:120°或75°或30°.
13、6㎝
三.解答题
14.解:(1)∵AB=AC,∠A=50°,∴∠ABC=∠C=(180°﹣∠A)=65°,
∵AB的垂直平分线DE,∴AE=BE,∴∠ABE=∠A=50°,
∴∠CBE=∠ABC﹣∠ABE=65°﹣50°=15°;
(2)∵△BCE的周长为9,BC=4,∴4+BE+CE=9,∵AE=BE,∴AE+CE=9﹣4=5,∴AC=5,
∵AB=AC,∴AB=5.
15.解:(1)∵DE⊥AB,DF⊥BC,∴∠DEB=∠DFB=90°,
∵∠EDF=124°,∴∠ABC=360°﹣90°﹣90°﹣124°=56°;
(2)∵BM平分∠ABC,DE⊥AB,DF⊥BC,∴ED=FD,∠EDB=∠FDB,∴∠EDP=∠FDP,
在△EDP和△FDP中,,∴△EDP≌△FDP(SAS),∴PE=PF.
16.解:(1)∵在△ABC中,AB=AC,∠A=40°,∴∠ABC=∠ACB=70°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,
∴∠NMB=90°﹣∠ABC=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,∴∠ABC=∠ACB=55°,
∵AB的垂直平分线交AB于点N,交BC的于点M,∴MN⊥AB,
∴∠NMB=90°﹣∠ABC=35°;
(3)∠NMB=∠A.
理由:∵在△ABC中,AB=AC,∴∠ABC=∠ACB=,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,
∴∠NMB=90°﹣∠ABC=∠A.
17.解:(1)∵倍角三角形的一个内角为150°,∴另两个内角的和是180°﹣150=30°,
∴另两个角的度数是20°和10°;
(2)设三角形两个相等角的度数是x,则顶角为2x或x,
∵x+x+2x=180°或2x+x=180°解得x=45°或72∴2x=90°,x=36°,
故它的顶角的度数是90°或36°.
(3)∵第(2)小题中等腰三角形是等腰直角三角形,设腰长为y,
∴2y2=42,
解得y=2cm,
故它的腰长为2cm.
求长度时忽略三边关系
1.已知等腰三角形两边长为3和7,则周长为( )
A.13 B.17 C.13或17 D.11
2.已知一个等腰三角形的三边长分别为2x﹣1、x+1、3x﹣2,求这个等腰三角形的周长.
(1)完成部分解题过程,在以下解答过程的空白处填上适当的内容.
解:①当2x﹣1=x+1时,解x= ,此时 构成三角形(填“能”或“不能”).
②当2x﹣1=3x﹣2时,解x= ,此时 构成三角形(填“能”或“不能”).
(2)请你根据(1)中两种情况的分类讨论,完成第三种情况的分析,若能构成等腰三角形,求出这个三角形的周长.
3.已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分,求这个等腰三角形的底边长和腰长.
当腰和底不明求角度时没有分类讨论
4.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
5.有一个三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则∠C的度数 。
6.等腰三角形一腰上的高与另一腰的夹角为35°,求这个三角形的各个内角的度数.
答案:
B.
2.解:(1)①当2x﹣1=x+1时,解x=2,此时3,3,4,能构成三角形.
②当2x﹣1=3x﹣2时,解x=1,此时1,2,1不能构成三角形.
故答案为2,能,1,不能;
(2)③当x+1=3x﹣2,解得x=,此时2,,能构成三角形,周长为7.
3.解:设三角形的腰为x,如图:
△ABC是等腰三角形,AB=AC,BD是AC边上的中线,
则有AB+AD=9或AB+AD=15,分下面两种情况解.
(1)x+x=9,∴x=6,∵三角形的周长为9+15=24cm, ∴三边长分别为6,6,12
∵6+6=12,不符合三角形的三边关系 ∴舍去;
(2)x+x=15 ∴x=10 ∵三角形的周长为24cm ∴三边长分别为10,10,4.
综上可知:这个等腰三角形的底边长为4cm,腰长为10cm.
4. C.
5.40°或25°或10°
6.解:①此等腰三角形为钝角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°, ∴此三角形的顶角=90°+35°=125°,
∴等腰三角形的各角的度数为125°,27.5°,27.5°;
②此等腰三角形为锐角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°,
∴此三角形的顶角=90°﹣35°=55°,
所以等腰三角形的各角的度数为55°,62.5°,62.5°.
等腰三角形中辅助线的作法
利用“三线合一”作辅助线
已知等腰作垂线(或中线、角平分线)
1.如图,在△ABC中,AB=AC,AE⊥BE于点E,且∠ABE=∠ABC. 若BE=2,则BC=_____.
2.如图所示,△ABC中,AB=AC,E在AC上,D在BA的延长线上,且AD=AE,连接DE.求证:DE⊥BC.
3.如图,△ABC中,AB=AC,D是BC的中点,过A点的直线EF∥BC,且AE=AF,求证:DE=DF.
4.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.
方法总结:当看到等腰三角形时要马上想到边相等,角相等,三线合一。解题技巧:①等腰三角形中有底边中点,常连底边上的中线解题;②遇等腰三角形说明图形中的垂线关系,常作底边上的高解题。
巧用“角平分线+垂线合一”构造等腰三角形(拓展)
拓展点拨:如图,△ABC中,AD平分∠BAC,AD⊥BC,由“ASA”易得△ABD≌△ACD ,从而得AB=AC,BD=CD。即一边上的高与这边所对的角平分线重合,易得这个三角形是等腰三角形。
5.已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.
求证:BD=2CE.
6.如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
(1)求证:∠BCN=∠CAE;
(2)求证:AE=CN+EN(请用多种方法证明)
7.已知,如图AB=AC,∠A=108°,BD平分∠ABC交AC于D,求证:BC=AB+CD.
方法总结:用截长补短法说明线段的和差关系:截长法:在长边上截取一条与某一条短边相等的线段,再说明剩下的线段与另一短边相等;补短法:延长短边得到与长边相等的线段,再说明延长线与另一短边相等。
答案:
4
2、证明:如图,过A作AM⊥BC于M,
∵AB=AC,∴∠BAC=2∠BAM,
∵AD=AE, ∴∠D=∠AED, ∴∠BAC=∠D+∠AED=2∠D, ∴∠BAC=2∠BAM=2∠D,
∴∠BAM=∠D, ∴DE∥AM,
∵AM⊥BC, ∴DE⊥BC.
3、证明:如图,连接AD.
∵△ABC中,AB=AC,D是BC的中点,∴AD⊥BC,
∵EF∥BC,∴AD⊥EF,又AE=AF,∴AD垂直平分EF,∴DE=DF.
4、证明:作EF⊥AC于F,
∵EA=EC,∴AF=FC=AC,∵AC=2AB,∴AF=AB,
∵AD平分∠BAC交BC于D,∴∠BAD=∠CAD,
在△BAE和△FAE中,∴△ABE≌△AFE(SAS),∴∠ABE=∠AFE=90°.
∴EB⊥AB.
5、证明:延长BA和CE交于点M,
∵CE⊥BD,∴∠BEC=∠BEM=90°,∵BD平分∠ABC,∴∠MBE=∠CBE,
在△BME和△BCE中,∴△BME≌△BCE(ASA),∴EM=EC=MC,
∵△ABC是等腰直角三角形,∴∠BAC=∠MAC=90°,BA=AC,∴∠ABD+∠BDA=90°,
∵∠BEC=90°,∴∠ACM+∠CBE=90°,
∵∠BDA=∠EDC,∴∠ABE=∠ACM,
在△ABD和△ACM中,∴△ABD≌△ACM(ASA),∴DB=MC,∴BD=2CE.
6、证明:(1)∵∠CAB=∠CBA=45°,∴∠ACB=90°,
∵CN⊥AE,∴∠COE=90°,∴∠CEA+∠1=90°,∠CEA+∠2=90°,∴∠BCN=∠CAE;
(2)法一:如图1,延长CN至F,使CF=AE,连接BF,
在△CAE和△BCF中,∴△CAE≌△BCF(SAS),∴∠ACE=∠CBF=90°,CE=BF,
∵∠CBA=45°,∴∠FBN=45°=∠EBN,∵E为BC中点,∴CE=BE=BF,
在△EBN和△FBN中,,∴△EBN≌△FBN(SAS),∴NE=NF,∴AE=CN+EN.
法二:如图2,在AE上截取AF=CN,
在△ACF和△CBN中,,∴△ACF≌△CBN,∴CF=BN,∠ACF=∠B=45°,
∴∠ECF=45°=∠B,
在△BEN和△CEF中,,∴△BEN≌△CEF,∴EN=EF,∴AE=AF+EF=CN+EN.
7、证明:在线段BC上截取BE=BA,连接DE.
∵BD平分∠ABC,∴∠ABD=∠EBD=∠ABC.
在△ABD和△EBD中,,∴△ABD≌△EBD.(SAS)
∴∠BED=∠A=108°,∠ADB=∠EDB.
又∵AB=AC,∠A=108°,∠ACB=∠ABC=×(180°﹣108°)=36°,
∴∠ABD=∠EBD=18°.∴∠ADB=∠EDB=180°﹣18°﹣108°=54°.
∴∠CDE=180°﹣∠ADB﹣∠EDB=180°﹣54°﹣54°=72°.
∴∠DEC=180°﹣∠DEB=180°﹣108°=72°.∴∠CDE=∠DEC.∴CD=CE.
∴BC=BE+EC=AB+CD.
等腰三角形与全等、垂直平分线、角平分线的综合
一.选择题
1.如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
A.55° B.45° C.35° D.65°
2.如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是( )
A.AD=BD B.BD=CD C.∠1=∠2 D.∠B=∠C
3.如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
A.13 B.15 C.17 D.19
4.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
A.45° B.50° C.51° D.52°
5.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
6.如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.① B.② C.①② D.①②③
8.等腰△ABC纸片(AB=AC)可按图中所示方法折成一个四边形,点A与点B重合,点C与点D重合,请问原等腰△ABC中的∠B=( )度.
A.48° B.60° C.72° D.80°
二.填空题
9.如图,是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上,AD和BC的关系为 .
10.如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 .
11.如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为 ,∠A的度数为 .
12.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
13.如图,△ABC中,∠ABC与∠ACB的外角平分线交于P,PM⊥AC于M,若PM=6cm,则点P到AB的距离为 .
三.解答题
14.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
(1)已知∠A=50°,求∠CBE的度数;
(2)已知△BCE的周长为9,BC=4,求AB的长.
15.如图,BM平分∠ABC,D是BM上一点,过点D作DE⊥AB,DF⊥BC,分别交AB于点E,交BC于点F,P是BM上的另一点,连接PE,PF.
(1)若∠EDF=124°,求∠ABC的度数;
(2)求证:PE=PF.
16.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现∠A与∠NMB有什么关系,试证明之.
17.如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”.例如,在△ABC中,如果∠A=50°,∠B=100°,那么△ABC就是一个“倍角三角形”.
(1)已知倍角三角形的一个内角为150°,求这个三角形的另两个角的度数;
(2)已知倍角三角形是一个等腰三角形,求它的顶角的度数;
(3)如果第(2)小题中等腰三角形的底边长为4cm,求它的腰长.
答案:
一.选择题
1、A. 2、A. 3、B. 4、A. 5、B. 6、C. 7、D. 8、C.
二.填空题
9.AD垂直平分BC.
10.9.
11.解:∵在△ABA1中,∠B=20°,AB=A1B,∴∠A=∠BA1A===80°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,∴∠CA2A1===40°;
同理可得,∠EA3A2=20°,
故答案为:20° 80°.
12.
解:∵∠AOB=60°,OC平分∠AOB,∴∠AOC=30°,
①当E在E1时,OE=CE,
∵∠AOC=∠OCE=30°,∴∠OEC=180°﹣30°﹣30°=120°;
②当E在E2点时,OC=OE,则∠OCE=∠OEC=(180°﹣30°)=75°;
③当E在E3时,OC=CE,则∠OEC=∠AOC=30°;
故答案为:120°或75°或30°.
13、6㎝
三.解答题
14.解:(1)∵AB=AC,∠A=50°,∴∠ABC=∠C=(180°﹣∠A)=65°,
∵AB的垂直平分线DE,∴AE=BE,∴∠ABE=∠A=50°,
∴∠CBE=∠ABC﹣∠ABE=65°﹣50°=15°;
(2)∵△BCE的周长为9,BC=4,∴4+BE+CE=9,∵AE=BE,∴AE+CE=9﹣4=5,∴AC=5,
∵AB=AC,∴AB=5.
15.解:(1)∵DE⊥AB,DF⊥BC,∴∠DEB=∠DFB=90°,
∵∠EDF=124°,∴∠ABC=360°﹣90°﹣90°﹣124°=56°;
(2)∵BM平分∠ABC,DE⊥AB,DF⊥BC,∴ED=FD,∠EDB=∠FDB,∴∠EDP=∠FDP,
在△EDP和△FDP中,,∴△EDP≌△FDP(SAS),∴PE=PF.
16.解:(1)∵在△ABC中,AB=AC,∠A=40°,∴∠ABC=∠ACB=70°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,
∴∠NMB=90°﹣∠ABC=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,∴∠ABC=∠ACB=55°,
∵AB的垂直平分线交AB于点N,交BC的于点M,∴MN⊥AB,
∴∠NMB=90°﹣∠ABC=35°;
(3)∠NMB=∠A.
理由:∵在△ABC中,AB=AC,∴∠ABC=∠ACB=,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,
∴∠NMB=90°﹣∠ABC=∠A.
17.解:(1)∵倍角三角形的一个内角为150°,∴另两个内角的和是180°﹣150=30°,
∴另两个角的度数是20°和10°;
(2)设三角形两个相等角的度数是x,则顶角为2x或x,
∵x+x+2x=180°或2x+x=180°解得x=45°或72∴2x=90°,x=36°,
故它的顶角的度数是90°或36°.
(3)∵第(2)小题中等腰三角形是等腰直角三角形,设腰长为y,
∴2y2=42,
解得y=2cm,
故它的腰长为2cm.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
