人教版八年级数学下册:18.2.3 正方形(第1课时)课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册:18.2.3 正方形(第1课时)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
思考以下问题
1、正方形四条边有什么关系?四个角呢?
2、正方形是矩形吗?是菱形吗?为什么?
3、我们应该怎样给正方形下定义呢?
4、正方形具有哪些性质?
B
A
C
D
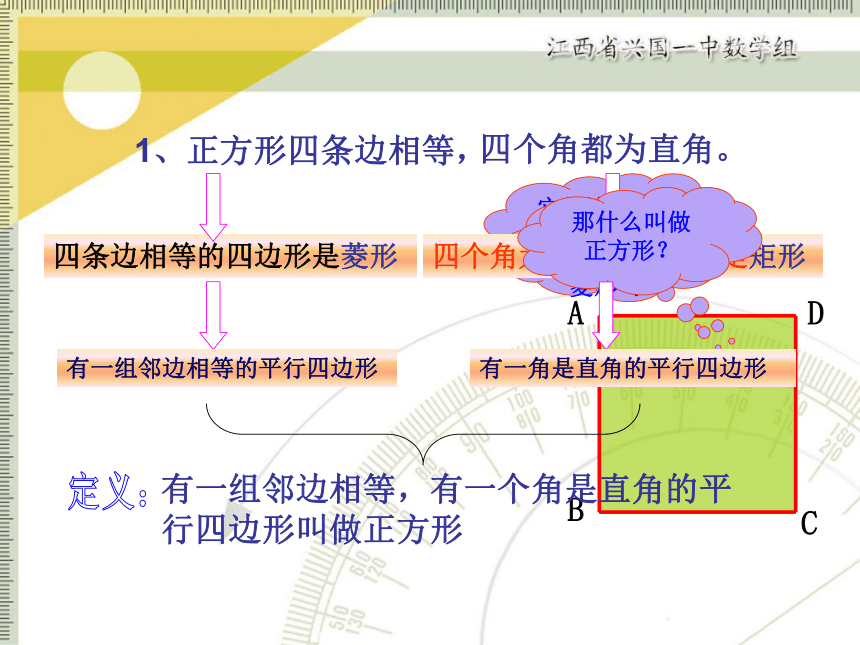
1、正方形四条边相等,
四个角都为直角。
它的边与角有什么关系?
它是矩形吗?它同时也是菱形吗?
四条边相等的四边形是菱形
四个角为直角的四边形是矩形
那什么叫做正方形?
有一组邻边相等的平行四边形
有一角是直角的平行四边形
有一组邻边相等,有一个角是直角的平行四边形叫做正方形
正方形有哪些性质呢
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
合作探究:正方形的性质
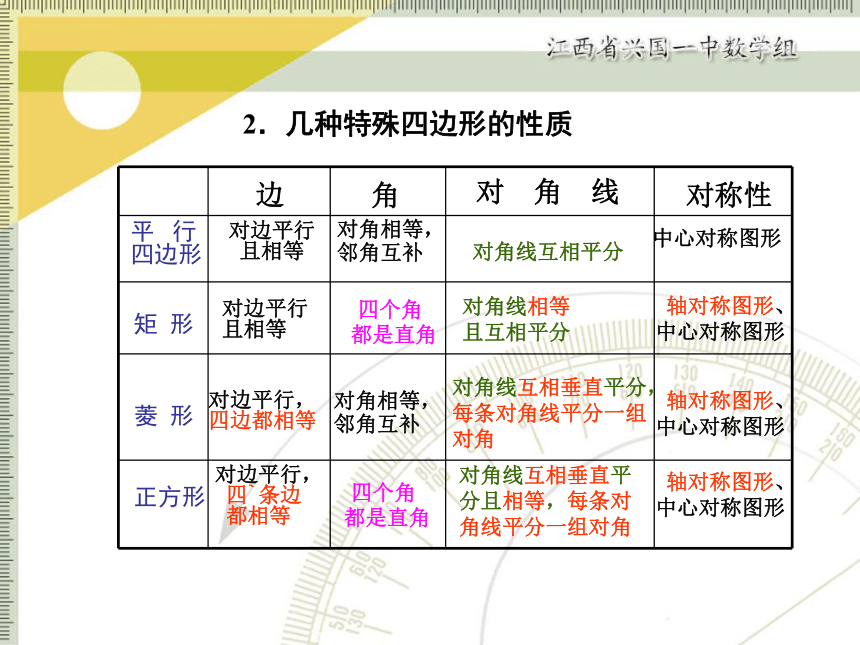
2.几种特殊四边形的性质
平 行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四边都相等
对边平行,
四`条边
都相等
角
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对 角 线
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
对称性
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
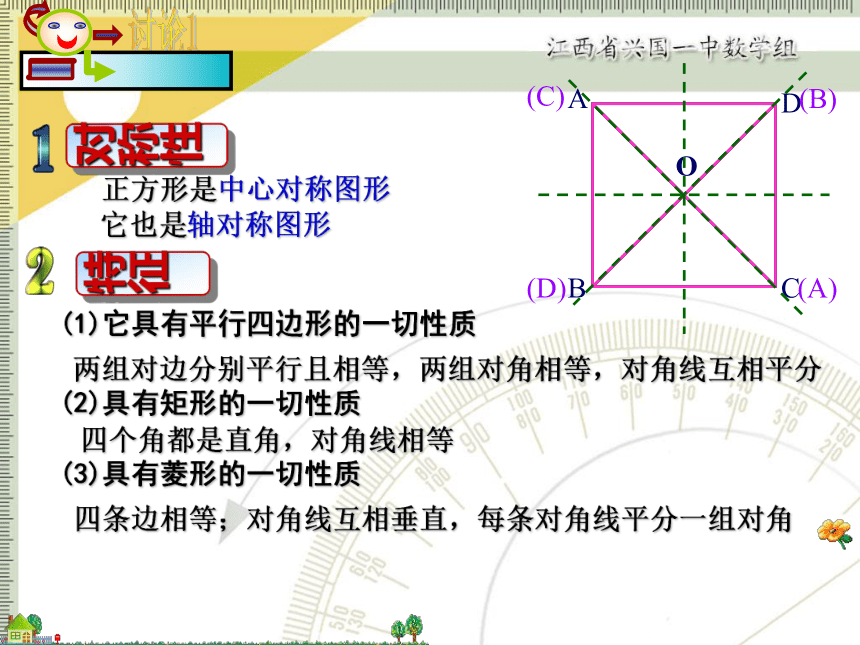
正方形是中心对称图形
它也是轴对称图形
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分
(2)具有矩形的一切性质
四个角都是直角,对角线相等
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角
(A)
(B)
(C)
(D)
例题1、如图,四边形ABCD是正方形,两条对角线相交于点O。
(1)一条对角线把它分成_______个全等的________ 三角形;
(2)图中一共有________个等腰直角三角形;两条对角线把它分成_______个全等的___________三角形;
(3)∠AOB=_____度,∠OAB=_____度.
二
等腰直角
四
等腰直角
八
45
90
(4)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
合作探究
合作探究
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,
AO=CO=BO=DO(正方形的两条对角线相等,并且互相垂直平分).
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
(4)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
你觉得什么样的平行四边形是正方形呢?
动
脑
想
一
想
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.平行四边形
有一组邻边相等
有一个角是直角
常
见
判
断
方
法
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
1.平行四边形
1、有一组邻边相等,有一个角是直角的平行四边形是正方形。 (以一般平行四边形为基础)
2、有一组邻边相等的矩形是正方形。 (以矩形为基础)
3、有一个角是直角的菱形是正方形。 (以菱形为基础)
1、判断以下说法是否正确,并说明理由:
②对角线互相垂直的矩形是正方形
③对角线相等的菱形是正方形
④对角线互相垂直平分且相等的四边形是正方形
想一想
① 对角线互相垂直且相等的四边形是正方形
2、已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
证明:∵ DE⊥BC,DF⊥AC, ∠C=90°
∴ 四边形CFDE是矩形
∵ CD平分∠ACB且 ∠ACB=90°
∴ 直角三角形DFC是等腰直角三角形
∴ CF=DF
∴ 四边形CFDE是正方形
你做对了吗?
一 展 身 手
定义
性质
有一组邻边相等,有一个角是直角的平行四边形叫做正方形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
对边平等且相等,四个角都是直角,两条结角线互相垂直一部分且相等,每条对角线平分一组对角。
判定
1、有一组邻边相等,有一个角是直角的平行四边形。
2、有一组邻边相等的矩形是正方形。
3、有一个角是直角的菱形是正方形。
平行四边形
矩形
菱形
正
方
形
正方形与矩形、菱形、平行四边形的关系
相互关系
如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
证明:∵四边形EFGH是正方形,
∴∠AFB=∠DEA=90, 且 ∠ABF+∠BAF=90,
又∵∠BAF+∠DAE=90, ∴∠ABF=∠DAE.
又∵AB=DA, ∴△ABF≌△DAE(AAS).
怎么用两条直线把一个正方形分成面积相等的四部分?
怎么用两条直线把一个正方形分成面积相等的四部分?
再见
思考以下问题
1、正方形四条边有什么关系?四个角呢?
2、正方形是矩形吗?是菱形吗?为什么?
3、我们应该怎样给正方形下定义呢?
4、正方形具有哪些性质?
B
A
C
D
1、正方形四条边相等,
四个角都为直角。
它的边与角有什么关系?
它是矩形吗?它同时也是菱形吗?
四条边相等的四边形是菱形
四个角为直角的四边形是矩形
那什么叫做正方形?
有一组邻边相等的平行四边形
有一角是直角的平行四边形
有一组邻边相等,有一个角是直角的平行四边形叫做正方形
正方形有哪些性质呢
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
合作探究:正方形的性质
2.几种特殊四边形的性质
平 行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四边都相等
对边平行,
四`条边
都相等
角
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对 角 线
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
对称性
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
正方形是中心对称图形
它也是轴对称图形
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分
(2)具有矩形的一切性质
四个角都是直角,对角线相等
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角
(A)
(B)
(C)
(D)
例题1、如图,四边形ABCD是正方形,两条对角线相交于点O。
(1)一条对角线把它分成_______个全等的________ 三角形;
(2)图中一共有________个等腰直角三角形;两条对角线把它分成_______个全等的___________三角形;
(3)∠AOB=_____度,∠OAB=_____度.
二
等腰直角
四
等腰直角
八
45
90
(4)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
合作探究
合作探究
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,
AO=CO=BO=DO(正方形的两条对角线相等,并且互相垂直平分).
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
(4)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
你觉得什么样的平行四边形是正方形呢?
动
脑
想
一
想
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.平行四边形
有一组邻边相等
有一个角是直角
常
见
判
断
方
法
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
1.平行四边形
1、有一组邻边相等,有一个角是直角的平行四边形是正方形。 (以一般平行四边形为基础)
2、有一组邻边相等的矩形是正方形。 (以矩形为基础)
3、有一个角是直角的菱形是正方形。 (以菱形为基础)
1、判断以下说法是否正确,并说明理由:
②对角线互相垂直的矩形是正方形
③对角线相等的菱形是正方形
④对角线互相垂直平分且相等的四边形是正方形
想一想
① 对角线互相垂直且相等的四边形是正方形
2、已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
证明:∵ DE⊥BC,DF⊥AC, ∠C=90°
∴ 四边形CFDE是矩形
∵ CD平分∠ACB且 ∠ACB=90°
∴ 直角三角形DFC是等腰直角三角形
∴ CF=DF
∴ 四边形CFDE是正方形
你做对了吗?
一 展 身 手
定义
性质
有一组邻边相等,有一个角是直角的平行四边形叫做正方形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
对边平等且相等,四个角都是直角,两条结角线互相垂直一部分且相等,每条对角线平分一组对角。
判定
1、有一组邻边相等,有一个角是直角的平行四边形。
2、有一组邻边相等的矩形是正方形。
3、有一个角是直角的菱形是正方形。
平行四边形
矩形
菱形
正
方
形
正方形与矩形、菱形、平行四边形的关系
相互关系
如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
证明:∵四边形EFGH是正方形,
∴∠AFB=∠DEA=90, 且 ∠ABF+∠BAF=90,
又∵∠BAF+∠DAE=90, ∴∠ABF=∠DAE.
又∵AB=DA, ∴△ABF≌△DAE(AAS).
怎么用两条直线把一个正方形分成面积相等的四部分?
怎么用两条直线把一个正方形分成面积相等的四部分?
再见
