人教版八年级数学 下册:20.1.1 平均数课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学 下册:20.1.1 平均数课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 524.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 20:49:33 | ||
图片预览






文档简介
(共24张PPT)
第二十章 数据的分析
人民教育出版社出版
日常生活中,我们常用平均数表示一组数据的“平均水平”
概念一:
一般地,对于n个数x1,x2,…,xn,我
们把
叫做这n个数的算术平均数,简称平均数.
计算某蓝球队11个队员的平均年龄:
平均年龄=
还有更简单的办法吗?
年龄
(岁) 26 28 29 30 31
相应队员数 1 3 1 4 2
计算某蓝球队11个队员的平均年龄:
方案二:
26+3×28+29+4×30+2×31
11
≈29.2(岁)
平均年龄=
年龄
(岁) 26 28 29 30 31
相应队员数 1 3 1 4 2
叫做这n个数的加权平均数.
数据的权能够反映的数据的相对“重要程度”.
上面的平均数29.2称为5个数26、28、29、30、31的加权平均数,1、3、1、4、2分别为5个数据的权
概念2
某市三个郊县的人数及人均耕地面积如下表:
问:这个市三个郊县的人均耕地面积是多少?(精确到0.01公顷)
小明求得这个市三个郊县的人均耕地面积为
应该是
你认为小明的做法有道理吗?为什么?
郊县 人数/万 人均耕地面积/公顷
A 15 0.15
B 7 0.21
C 10 0.18
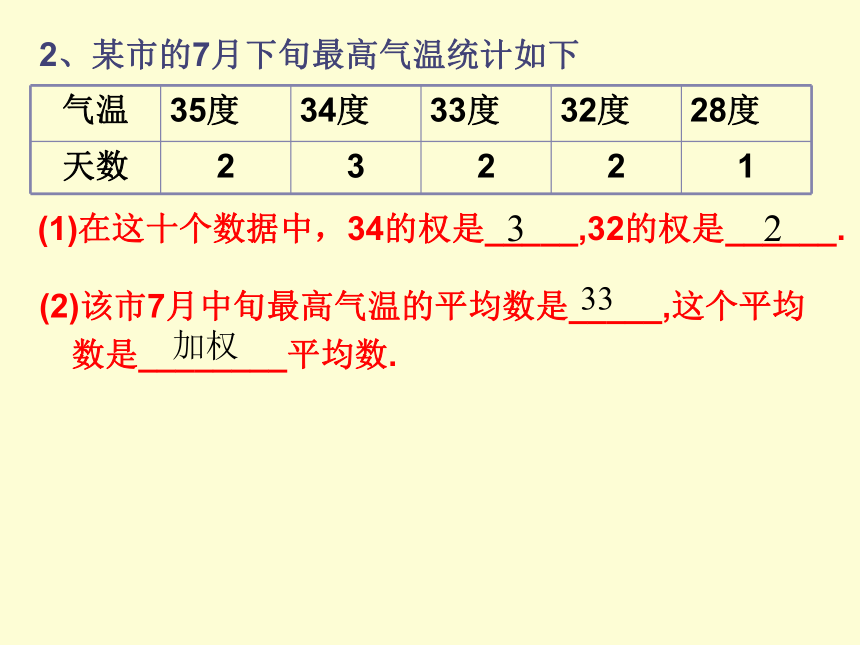
2、某市的7月下旬最高气温统计如下
(1)在这十个数据中,34的权是_____,32的权是______.
3
2
(2)该市7月中旬最高气温的平均数是_____,这个平均数是________平均数.
33
加权
气温 35度 34度 33度 32度 28度
天数 2 3 2 2 1
一家公司对甲、乙二名应聘者进行了听、说、读、写的英语水平测试,他们的成绩如下表所示:
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写按照2:2:3:3的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写按照3:3:2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
录取甲
录取乙
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
总结:
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时,往往给每个数据一个“ 权 ”。如例一(1)中听、说、读、写的权分别是3,3,2,2
(2)中听、说、读、写的权分别是2,2,3,3
导致最终录取结果的不同。
例2 一次演讲比赛中,评委将从演讲内容,演讲能力,演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次。
活动3
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
权 50% 40% 10%
你能说说算术平均数与加权平均数的区别和联系吗?
2、在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数。
1、算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等)
习题
1、某班进行个人投篮比赛,受了污损的下表记录了在规定时间内投进n个球的人数分布情况:
同时,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均投进2.5个球,问投进3个球和4个球的各有多少人?
进球数n 0 1 2 3 4 5
投进n球的人数 1 2 7 2
2.某公司要招聘一名市场部经理,要对应聘人员进行三项测试 :语言表达、微机操作、商品知识、成绩的权分别是3、4、3,现有A、B、C、三人的测试成绩如下,你通过计算分析谁会被录用?
假如要使B被录用请你重新设计各种成绩的权,并说明决定的正确性。
答案不唯一,你可以尽情的发挥,只要合理就可以
语言表达 微机操作 商品知识
A 60 80 70
B 50 70 80
C 60 80 65
例.为了了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这天5路公共汽车平均每班的载客量是多少?
组中值是小组两个端点数的平均数。
载客量/人 组中值 频数(班次)
1≤X<21 11 3
21≤X<41 31 5
41≤X<61 51 20
61≤X<81 71 22
81 ≤X<101 91 18
101≤X<121 111 15
从表中,可求出这一天5路公共汽车平均每班载客量。你能知道大约有多少班次的载客量在平均载客量以上呢?占全天总班次的百分比是多少?
有33班次载客量在平均载客量以上;
载客量/人 组中值 频数(班次)
1≤X<21 11 3
21 ≤X<41 31 5
41 ≤X<61 51 20
61 ≤X<81 71 22
81 ≤X<101 91 18
101≤X<121 111 15
1:某灯泡厂为了测量一批灯泡的使用寿命,从中抽查了50只灯泡,它们的使用表所示:
这批灯泡的平均使用寿命是多少?
使用寿命/时 600
≦x<
1000 1000≦x<
1400 1400≦x<
1800 1800
≦x<
2200 2200
≦ x <
2600
灯泡数/个 5 10 12 17 6
2、某校为了了解学生作课外作业所用时间的情况,对学生作课外作业所用时间进行调查,下表是该校初二某班50名学生某一天做数学课外作业所用时间的情况统计表
(1)第二组数据的组中值是多少?
(2)求该班学生平均每天做数学作业所用时间
所用时间t(分钟) 人数
0<t≤10 4
10<t≤20 6
20<t≤30 14
30<t≤40 13
40<t≤50 9
50<t≤60 4
第二十章 数据的分析
人民教育出版社出版
日常生活中,我们常用平均数表示一组数据的“平均水平”
概念一:
一般地,对于n个数x1,x2,…,xn,我
们把
叫做这n个数的算术平均数,简称平均数.
计算某蓝球队11个队员的平均年龄:
平均年龄=
还有更简单的办法吗?
年龄
(岁) 26 28 29 30 31
相应队员数 1 3 1 4 2
计算某蓝球队11个队员的平均年龄:
方案二:
26+3×28+29+4×30+2×31
11
≈29.2(岁)
平均年龄=
年龄
(岁) 26 28 29 30 31
相应队员数 1 3 1 4 2
叫做这n个数的加权平均数.
数据的权能够反映的数据的相对“重要程度”.
上面的平均数29.2称为5个数26、28、29、30、31的加权平均数,1、3、1、4、2分别为5个数据的权
概念2
某市三个郊县的人数及人均耕地面积如下表:
问:这个市三个郊县的人均耕地面积是多少?(精确到0.01公顷)
小明求得这个市三个郊县的人均耕地面积为
应该是
你认为小明的做法有道理吗?为什么?
郊县 人数/万 人均耕地面积/公顷
A 15 0.15
B 7 0.21
C 10 0.18
2、某市的7月下旬最高气温统计如下
(1)在这十个数据中,34的权是_____,32的权是______.
3
2
(2)该市7月中旬最高气温的平均数是_____,这个平均数是________平均数.
33
加权
气温 35度 34度 33度 32度 28度
天数 2 3 2 2 1
一家公司对甲、乙二名应聘者进行了听、说、读、写的英语水平测试,他们的成绩如下表所示:
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写按照2:2:3:3的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写按照3:3:2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
录取甲
录取乙
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
总结:
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时,往往给每个数据一个“ 权 ”。如例一(1)中听、说、读、写的权分别是3,3,2,2
(2)中听、说、读、写的权分别是2,2,3,3
导致最终录取结果的不同。
例2 一次演讲比赛中,评委将从演讲内容,演讲能力,演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次。
活动3
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
权 50% 40% 10%
你能说说算术平均数与加权平均数的区别和联系吗?
2、在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数。
1、算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等)
习题
1、某班进行个人投篮比赛,受了污损的下表记录了在规定时间内投进n个球的人数分布情况:
同时,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均投进2.5个球,问投进3个球和4个球的各有多少人?
进球数n 0 1 2 3 4 5
投进n球的人数 1 2 7 2
2.某公司要招聘一名市场部经理,要对应聘人员进行三项测试 :语言表达、微机操作、商品知识、成绩的权分别是3、4、3,现有A、B、C、三人的测试成绩如下,你通过计算分析谁会被录用?
假如要使B被录用请你重新设计各种成绩的权,并说明决定的正确性。
答案不唯一,你可以尽情的发挥,只要合理就可以
语言表达 微机操作 商品知识
A 60 80 70
B 50 70 80
C 60 80 65
例.为了了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这天5路公共汽车平均每班的载客量是多少?
组中值是小组两个端点数的平均数。
载客量/人 组中值 频数(班次)
1≤X<21 11 3
21≤X<41 31 5
41≤X<61 51 20
61≤X<81 71 22
81 ≤X<101 91 18
101≤X<121 111 15
从表中,可求出这一天5路公共汽车平均每班载客量。你能知道大约有多少班次的载客量在平均载客量以上呢?占全天总班次的百分比是多少?
有33班次载客量在平均载客量以上;
载客量/人 组中值 频数(班次)
1≤X<21 11 3
21 ≤X<41 31 5
41 ≤X<61 51 20
61 ≤X<81 71 22
81 ≤X<101 91 18
101≤X<121 111 15
1:某灯泡厂为了测量一批灯泡的使用寿命,从中抽查了50只灯泡,它们的使用表所示:
这批灯泡的平均使用寿命是多少?
使用寿命/时 600
≦x<
1000 1000≦x<
1400 1400≦x<
1800 1800
≦x<
2200 2200
≦ x <
2600
灯泡数/个 5 10 12 17 6
2、某校为了了解学生作课外作业所用时间的情况,对学生作课外作业所用时间进行调查,下表是该校初二某班50名学生某一天做数学课外作业所用时间的情况统计表
(1)第二组数据的组中值是多少?
(2)求该班学生平均每天做数学作业所用时间
所用时间t(分钟) 人数
0<t≤10 4
10<t≤20 6
20<t≤30 14
30<t≤40 13
40<t≤50 9
50<t≤60 4
