沪科版九年级下册数学25.2三视图同步练习(无答案)
文档属性
| 名称 | 沪科版九年级下册数学25.2三视图同步练习(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览

文档简介
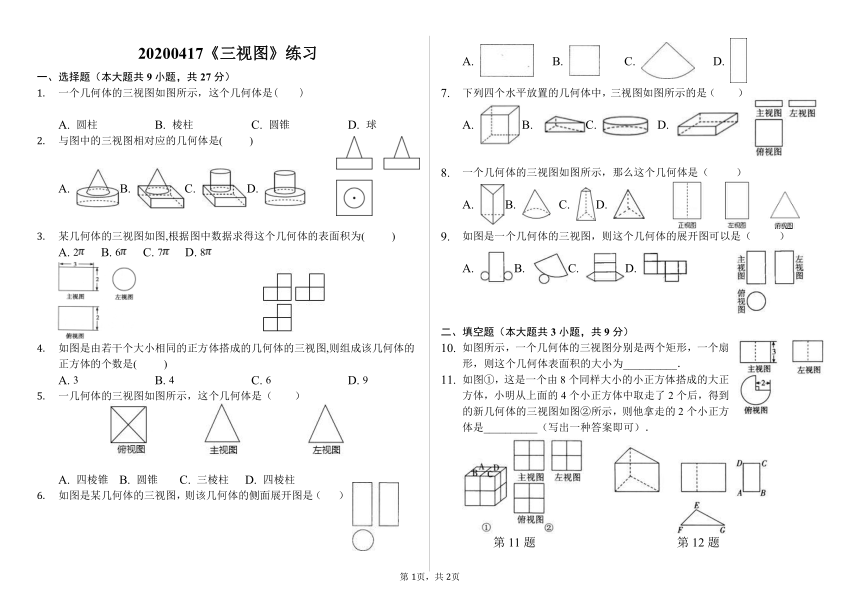
20200417《三视图》练习
一、选择题(本大题共9小题,共27分)
1. 一个几何体的三视图如图所示,这个几何体是( )
A. 圆柱 B. 棱柱 C. 圆锥 D. 球
2. 与图中的三视图相对应的几何体是( )
A. B. C. D.
3. 某几何体的三视图如图,根据图中数据求得这个几何体的表面积为( )
A. 2 B. 6 C. 7 D. 8
4. 如图是由若干个大小相同的正方体搭成的几何体的三视图,则组成该几何体的正方体的个数是( )
A. 3 B. 4 C. 6 D. 9
5. 一几何体的三视图如图所示,这个几何体是( )
A. 四棱锥 B. 圆锥 C. 三棱柱 D. 四棱柱
6. 如图是某几何体的三视图,则该几何体的侧面展开图是( )
A. B. C. D.
7. 下列四个水平放置的几何体中,三视图如图所示的是( )
A. B. C. D.
8. 一个几何体的三视图如图所示,那么这个几何体是( )
A. B. C. D.
9. 如图是一个几何体的三视图,则这个几何体的展开图可以是( )
A. B. C. D.
二、填空题(本大题共3小题,共9分)
10. 如图所示,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为__________.
11. 如图①,这是一个由8个同样大小的小正方体搭成的大正方体,小明从上面的4个小正方体中取走了2个后,得到的新几何体的三视图如图②所示,则他拿走的2个小正方体是__________(写出一种答案即可).
第11题 第12题
12. 三棱柱的三视图如图所示,已知△EFG中,EF=8 cm,FG=12 cm,∠EFG=45°,则AB的长为_________cm.
三、解答题(本大题共5小题,共40分)
13. 画出如图所示立体图形的三视图.
14. 如图所示为一个几何体的三视图(单位:cm).
(1)组成该几何体的两部分分别是什么几何体?
(2)求该几何体的体积.(保留3位有效数字)
15. 如图,这是由7个棱长为1的正方体组成的几何体,画出其三视图并计算其表面积.
16. 如图是一个包装纸盒的三视图(单位:cm).
(1)该包装纸盒的几何形状是__________;
(2)画出该纸盒的展开图;
(3)制作一个这样的纸盒所需纸板的面积为__________.(结果精确到1 cm2)
17. 如图为一个立方体和它的三视图,完成下面的填空.
(1)棱AD在正投影面上的正投影是________,在水平投影面上的正投影是________;
( 2)侧面BCC1B1在正投影面上的正投影是________,在侧投影面上的正投影是________.
第2页,共2页
第1页,共1页
一、选择题(本大题共9小题,共27分)
1. 一个几何体的三视图如图所示,这个几何体是( )
A. 圆柱 B. 棱柱 C. 圆锥 D. 球
2. 与图中的三视图相对应的几何体是( )
A. B. C. D.
3. 某几何体的三视图如图,根据图中数据求得这个几何体的表面积为( )
A. 2 B. 6 C. 7 D. 8
4. 如图是由若干个大小相同的正方体搭成的几何体的三视图,则组成该几何体的正方体的个数是( )
A. 3 B. 4 C. 6 D. 9
5. 一几何体的三视图如图所示,这个几何体是( )
A. 四棱锥 B. 圆锥 C. 三棱柱 D. 四棱柱
6. 如图是某几何体的三视图,则该几何体的侧面展开图是( )
A. B. C. D.
7. 下列四个水平放置的几何体中,三视图如图所示的是( )
A. B. C. D.
8. 一个几何体的三视图如图所示,那么这个几何体是( )
A. B. C. D.
9. 如图是一个几何体的三视图,则这个几何体的展开图可以是( )
A. B. C. D.
二、填空题(本大题共3小题,共9分)
10. 如图所示,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为__________.
11. 如图①,这是一个由8个同样大小的小正方体搭成的大正方体,小明从上面的4个小正方体中取走了2个后,得到的新几何体的三视图如图②所示,则他拿走的2个小正方体是__________(写出一种答案即可).
第11题 第12题
12. 三棱柱的三视图如图所示,已知△EFG中,EF=8 cm,FG=12 cm,∠EFG=45°,则AB的长为_________cm.
三、解答题(本大题共5小题,共40分)
13. 画出如图所示立体图形的三视图.
14. 如图所示为一个几何体的三视图(单位:cm).
(1)组成该几何体的两部分分别是什么几何体?
(2)求该几何体的体积.(保留3位有效数字)
15. 如图,这是由7个棱长为1的正方体组成的几何体,画出其三视图并计算其表面积.
16. 如图是一个包装纸盒的三视图(单位:cm).
(1)该包装纸盒的几何形状是__________;
(2)画出该纸盒的展开图;
(3)制作一个这样的纸盒所需纸板的面积为__________.(结果精确到1 cm2)
17. 如图为一个立方体和它的三视图,完成下面的填空.
(1)棱AD在正投影面上的正投影是________,在水平投影面上的正投影是________;
( 2)侧面BCC1B1在正投影面上的正投影是________,在侧投影面上的正投影是________.
第2页,共2页
第1页,共1页
