2020年九年级数学中考二轮专题复习:胡不归和阿氏圆问题学案(无答案)
文档属性
| 名称 | 2020年九年级数学中考二轮专题复习:胡不归和阿氏圆问题学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览




文档简介
2020年中考复习专题:“胡不归”问题
在前面的最值问题中往往都是求某个线段最值或者形如PA+PB最值,除此之外我们还可能会遇上形如“PA+kPB”这样的式子的最值,此类式子一般可以分为两类问题:
(1)胡不归问题;
(2)阿氏圆.
本文简单介绍“胡不归”模型
【故事介绍】
从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家,根据“两点之间线段最短”,虽然从他此刻位置A到家B之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”(“胡”同“何”)
而如果先沿着驿道AC先走一段,再走砂石地,会不会更早到家?
【模型建立】
如图,一动点P在直线MN外的运动速度为V1,在直线MN上运动的速度为V2,且V1<V2,A、B为定点,点C在直线MN上,确定点C的位置使的值最小
【问题分析】
,记 ,即求BC+kAC的最小值
【问题解决】
构造射线AD使得sin∠DAN=k,,CH=kAC.
将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小.
【模型总结】
在求形如“PA+kPB"的式子的最值问题中,关键是构造与kPB相等的线段,将“PH+kPB”型
问题转化为“PA+PC”型.
而这里的PB必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB的等线段.
【2019长沙中考】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE
上的一个动点,则CD+的最小值是
【2019南通中考】如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则PB+PD的最小值等于
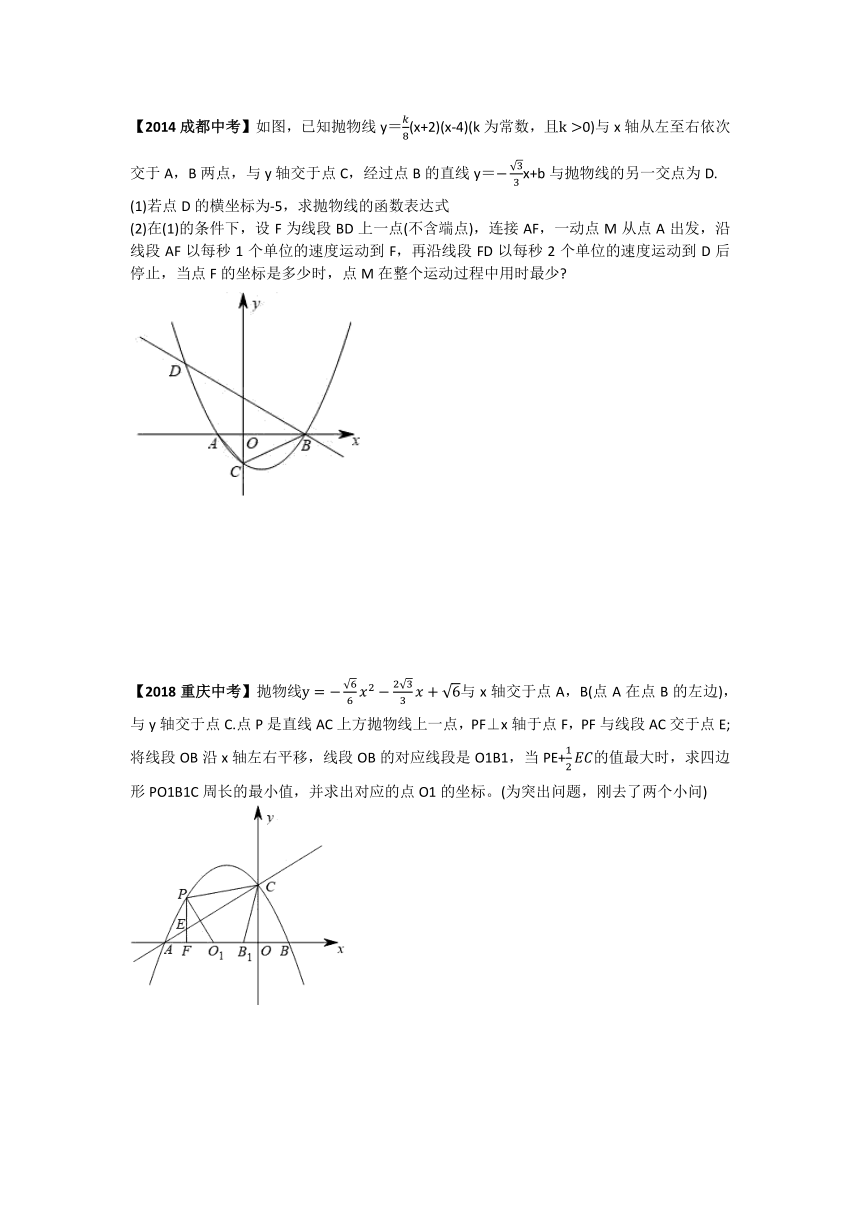
【2014成都中考】如图,已知抛物线y=(x+2)(x-4)(k为常数,且0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=x+b与抛物线的另一交点为D.
(1)若点D的横坐标为-5,求抛物线的函数表达式
(2)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
【2018重庆中考】抛物线与x轴交于点A,B(点A在点B的左边),与y轴交于点C.点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标。(为突出问题,刚去了两个小问)
【2019绵阳中考】在平面直角坐标系中,将二次函数 (a>0)的图象向右平移1个单位,再向下半移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧),OA=1经过点A的一次函数y=kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标;
(3)若点P为x轴上任意一点,在(2)的结论下,求PE+PA的最小值
阿氏圆问题
在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中P点轨迹是直线,而当P点轨迹变为圆时,即通常我们所说的“阿氏圆”问题
所谓“阿氏圆”,是指由古希腊数学家阿波罗尼奥斯提出的的概念,在平面内,到两个定点距离之比等于定值(不为1)的点的集合叫做圆
如下图,已知A、B两点,点P满足PA:PB=k(k≠1),则满足条件的所有的点P构成的图形为圆
下面给出证明
法一:首先了解两个定理
(1)角平分线定理:如图,在△ABC中,AD是∠BAC的角半分线,则
证明:,,即
(2)外角半分线定理:如图,在△ABC中,外角CAE的角平分线AD交BC的延长线于点D,则
证明:在BA延长线上取点E使得AE=AC,连接BD,则△ACD△AED(SAS),
CD=DE且AD平分∠BDE,则,即.
接下来开始阿氏圆证明步骤:
如图,PA:PB=k,作∠APB的角平分线交AB于M点,根据角平分线定理,,
故M点为定点,即∠APB的角平分线交AB于定点;
作∠APB外角平分线交直线AB于N点,根据外角平分线定理,,
故N点为定点,即∠APB外角半分线交直线AB于定点;
又∠MPN=90°,定边对定角,故P点轨迹是以MN为直径的圆。
法二:建系
不妨将点A、B两点置于x轴上且关于原点对称,设A(-m,0),则B(m,0),设P(x,y),PA=kPB,即:
解析式满足圆的一般方程,故P点所构成的图形是圆,且圆心与AB共线除了证明之外,我们还需了解“阿氏圆”的一些性质:
(1)
应用:根据点A、B的位置及k的值可确定M、N及圆心O
(2)△OBP∽△OPA,即,变形为OP2=OAOB.
应用:根据圆心及半径和A、B其中一点,可求A、B另外一点位置
(3)
应用:已知半径及A、B中的其中一点,即可知道PA:PB的值
练习1:已知A、B求圆轨迹
已知在坐标系中,点A(-1,0),点B(3,0),P是平面中一点且PA:PB=3:1,求P点轨迹圆圆心位置
【分析】
既然已经了解的“阿氏圆”的相关内容,不妨直接用上结论.
取M(2,0)满足MA:MB=3:1,取N(5,0)满足NA:NB=3:1,
P点轨迹即是以MN为直径,MN中点O为圆心的圆.
练习2:已知圆轨迹反求点A或B
已知在坐标系中,点A(-1,0),P是以点A()为圆心,长为半径的圆。平面中求一点
B使得PA:PB=3:1,求B点坐标.
【分析】
像这样的问题一般就是“阿氏圆”构图,已知圆与A点,求另外一点B.
思路1:构造相似三角形。
考虑OP2=OAOB,将OP=、OA=代入可得:OB=,故B点坐标为(3,0)
思路2:根据“阿氏圆”中的特殊位置
当P点运动到M点位置时,有MA:MB=3:1,考虑到A(-1,0)、M(2,0),可得MB=1,
考虑到A、M、B共线且B点在M点右侧,
可得B点坐标为(3,0).
补充:这里的圆O与点A及PA:PB的比值都是配套存在的,思路2虽有投机取巧之嫌,却是根据“阿氏圆”定义求出的B点,还好用。
那么这个玩意和最值有什么关系呢?
比如可以将练习2稍加修改,即可变成最值问题:
练习2(改):已知在坐标系中,点A(1,0),P是以点()为圆心,长为半径的圆,
Q(2,2),求PQ+PA的最小值.
【分析】
问题中的PQ暂时不用管,先处理好PA,考感到P点轨是个圆,且要构造PA,大胆猜测:平面中存在一点B使得P在圆上任意位置,均满足:,即有PB=PA.
其实就是逆用“阿氏圆”,这样的题目一般就是给出圆与A点位置,求另一点B的位置可转化PA.
点B求法如上练习2,剩下的求量小值就很简单了
练习3:关于系数
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,2为半径作圆,分別交
AC、BC于D、E两点,点P是圆C上一个动点,则PA+PB的最小值为
【分析】确定了问题关键是构造“PA",已知了P点所在的,已知了A点,即在平面中找一点M使得“PM=PA”
思路1:构造相似三角形
点M与A、C共线,且M点必满足:CP2=CMCA,
代入CP、CA,即可得:22=4CM,得:CM=1,即可确定M点位置,
PA+PB=PM+PB问题转化为PM+PB最小值,直接连BM即可
【问题剖析】
(1)这里为什么是PA?
答:因为圆C半径为2,CA=4,比值是1:2,△CMP与△CPA的相似比为1:2所以构造的是PA,也只能构造PA
(2)如果问题设计为PA+kPB最小值,k应为多少?
答:根据圆C半径与CB之比为2:3,k应为.
【练习1】如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则2AD+3BD的最小值是
问题转化为DM+DB的最小值,直接连接BM,BM长度的3倍即为本题答案
【练习2】、如图,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,则PDPC的最大值为
【分析】当P点运动到BC边上时,此时PC=2,根据题意要求构造PC,在BC上取M,使得此时PM=1,则在点P运动的任意时刻,均有PM=PC,从而将同题转化为求PDPM
连接PD,对于△PDM, PD-PM<DM,故当D、M、P共线时,PDPM=DM为最大值
【2019山东日照第22题】
如图1,在平面直角坐标系中,直线y=5x+5与x轴、y轴分別交于A、C两点,抛物线经过A、C两点,与x轴的另一交点为B.
(1)求抛物线解析式及B点坐标;
(2)若点M为x轴下方抛物线上一动点,连接MA、MB、MC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;
(3)如图2,若P点是半径为2的圆B上一动点,连接PC、PA,当点P运动到某一位置时,PC+PA的值最小,请求出这个最小值,并说明理由.
在前面的最值问题中往往都是求某个线段最值或者形如PA+PB最值,除此之外我们还可能会遇上形如“PA+kPB”这样的式子的最值,此类式子一般可以分为两类问题:
(1)胡不归问题;
(2)阿氏圆.
本文简单介绍“胡不归”模型
【故事介绍】
从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家,根据“两点之间线段最短”,虽然从他此刻位置A到家B之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”(“胡”同“何”)
而如果先沿着驿道AC先走一段,再走砂石地,会不会更早到家?
【模型建立】
如图,一动点P在直线MN外的运动速度为V1,在直线MN上运动的速度为V2,且V1<V2,A、B为定点,点C在直线MN上,确定点C的位置使的值最小
【问题分析】
,记 ,即求BC+kAC的最小值
【问题解决】
构造射线AD使得sin∠DAN=k,,CH=kAC.
将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小.
【模型总结】
在求形如“PA+kPB"的式子的最值问题中,关键是构造与kPB相等的线段,将“PH+kPB”型
问题转化为“PA+PC”型.
而这里的PB必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB的等线段.
【2019长沙中考】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE
上的一个动点,则CD+的最小值是
【2019南通中考】如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则PB+PD的最小值等于
【2014成都中考】如图,已知抛物线y=(x+2)(x-4)(k为常数,且0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=x+b与抛物线的另一交点为D.
(1)若点D的横坐标为-5,求抛物线的函数表达式
(2)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
【2018重庆中考】抛物线与x轴交于点A,B(点A在点B的左边),与y轴交于点C.点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标。(为突出问题,刚去了两个小问)
【2019绵阳中考】在平面直角坐标系中,将二次函数 (a>0)的图象向右平移1个单位,再向下半移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧),OA=1经过点A的一次函数y=kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标;
(3)若点P为x轴上任意一点,在(2)的结论下,求PE+PA的最小值
阿氏圆问题
在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中P点轨迹是直线,而当P点轨迹变为圆时,即通常我们所说的“阿氏圆”问题
所谓“阿氏圆”,是指由古希腊数学家阿波罗尼奥斯提出的的概念,在平面内,到两个定点距离之比等于定值(不为1)的点的集合叫做圆
如下图,已知A、B两点,点P满足PA:PB=k(k≠1),则满足条件的所有的点P构成的图形为圆
下面给出证明
法一:首先了解两个定理
(1)角平分线定理:如图,在△ABC中,AD是∠BAC的角半分线,则
证明:,,即
(2)外角半分线定理:如图,在△ABC中,外角CAE的角平分线AD交BC的延长线于点D,则
证明:在BA延长线上取点E使得AE=AC,连接BD,则△ACD△AED(SAS),
CD=DE且AD平分∠BDE,则,即.
接下来开始阿氏圆证明步骤:
如图,PA:PB=k,作∠APB的角平分线交AB于M点,根据角平分线定理,,
故M点为定点,即∠APB的角平分线交AB于定点;
作∠APB外角平分线交直线AB于N点,根据外角平分线定理,,
故N点为定点,即∠APB外角半分线交直线AB于定点;
又∠MPN=90°,定边对定角,故P点轨迹是以MN为直径的圆。
法二:建系
不妨将点A、B两点置于x轴上且关于原点对称,设A(-m,0),则B(m,0),设P(x,y),PA=kPB,即:
解析式满足圆的一般方程,故P点所构成的图形是圆,且圆心与AB共线除了证明之外,我们还需了解“阿氏圆”的一些性质:
(1)
应用:根据点A、B的位置及k的值可确定M、N及圆心O
(2)△OBP∽△OPA,即,变形为OP2=OAOB.
应用:根据圆心及半径和A、B其中一点,可求A、B另外一点位置
(3)
应用:已知半径及A、B中的其中一点,即可知道PA:PB的值
练习1:已知A、B求圆轨迹
已知在坐标系中,点A(-1,0),点B(3,0),P是平面中一点且PA:PB=3:1,求P点轨迹圆圆心位置
【分析】
既然已经了解的“阿氏圆”的相关内容,不妨直接用上结论.
取M(2,0)满足MA:MB=3:1,取N(5,0)满足NA:NB=3:1,
P点轨迹即是以MN为直径,MN中点O为圆心的圆.
练习2:已知圆轨迹反求点A或B
已知在坐标系中,点A(-1,0),P是以点A()为圆心,长为半径的圆。平面中求一点
B使得PA:PB=3:1,求B点坐标.
【分析】
像这样的问题一般就是“阿氏圆”构图,已知圆与A点,求另外一点B.
思路1:构造相似三角形。
考虑OP2=OAOB,将OP=、OA=代入可得:OB=,故B点坐标为(3,0)
思路2:根据“阿氏圆”中的特殊位置
当P点运动到M点位置时,有MA:MB=3:1,考虑到A(-1,0)、M(2,0),可得MB=1,
考虑到A、M、B共线且B点在M点右侧,
可得B点坐标为(3,0).
补充:这里的圆O与点A及PA:PB的比值都是配套存在的,思路2虽有投机取巧之嫌,却是根据“阿氏圆”定义求出的B点,还好用。
那么这个玩意和最值有什么关系呢?
比如可以将练习2稍加修改,即可变成最值问题:
练习2(改):已知在坐标系中,点A(1,0),P是以点()为圆心,长为半径的圆,
Q(2,2),求PQ+PA的最小值.
【分析】
问题中的PQ暂时不用管,先处理好PA,考感到P点轨是个圆,且要构造PA,大胆猜测:平面中存在一点B使得P在圆上任意位置,均满足:,即有PB=PA.
其实就是逆用“阿氏圆”,这样的题目一般就是给出圆与A点位置,求另一点B的位置可转化PA.
点B求法如上练习2,剩下的求量小值就很简单了
练习3:关于系数
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,2为半径作圆,分別交
AC、BC于D、E两点,点P是圆C上一个动点,则PA+PB的最小值为
【分析】确定了问题关键是构造“PA",已知了P点所在的,已知了A点,即在平面中找一点M使得“PM=PA”
思路1:构造相似三角形
点M与A、C共线,且M点必满足:CP2=CMCA,
代入CP、CA,即可得:22=4CM,得:CM=1,即可确定M点位置,
PA+PB=PM+PB问题转化为PM+PB最小值,直接连BM即可
【问题剖析】
(1)这里为什么是PA?
答:因为圆C半径为2,CA=4,比值是1:2,△CMP与△CPA的相似比为1:2所以构造的是PA,也只能构造PA
(2)如果问题设计为PA+kPB最小值,k应为多少?
答:根据圆C半径与CB之比为2:3,k应为.
【练习1】如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则2AD+3BD的最小值是
问题转化为DM+DB的最小值,直接连接BM,BM长度的3倍即为本题答案
【练习2】、如图,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,则PDPC的最大值为
【分析】当P点运动到BC边上时,此时PC=2,根据题意要求构造PC,在BC上取M,使得此时PM=1,则在点P运动的任意时刻,均有PM=PC,从而将同题转化为求PDPM
连接PD,对于△PDM, PD-PM<DM,故当D、M、P共线时,PDPM=DM为最大值
【2019山东日照第22题】
如图1,在平面直角坐标系中,直线y=5x+5与x轴、y轴分別交于A、C两点,抛物线经过A、C两点,与x轴的另一交点为B.
(1)求抛物线解析式及B点坐标;
(2)若点M为x轴下方抛物线上一动点,连接MA、MB、MC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;
(3)如图2,若P点是半径为2的圆B上一动点,连接PC、PA,当点P运动到某一位置时,PC+PA的值最小,请求出这个最小值,并说明理由.
同课章节目录
