河南省平顶山市第一中学2019-2020学年高二下学期开学考试数学(理)试题 Word版含答案
文档属性
| 名称 | 河南省平顶山市第一中学2019-2020学年高二下学期开学考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 395.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 23:33:47 | ||
图片预览




文档简介
2019~2020学年下学期高二质量检测(四)
高二理科数学
第Ⅰ卷
一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项.
1.已知复数z=,则“θ=”是“z是纯虚数”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
2. “干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅、…、癸酉,甲戌、乙亥、丙子、…、癸未,甲申、乙酉、丙戌、…、癸巳,…、癸亥,共得到60个组合,称六十甲子,周而复始,无穷无尽.2019年是“干支纪年法”中的己亥年,那么2026年是“干支纪年法”中的( )
A.甲辰年 B.乙巳年 C.丙午年 D.丁未年
3. 某面粉供应商所供应的某种袋装面粉质量(单位:kg)服从正态分布N(10,0.12),现抽取500袋样本,X表示抽取的面粉质量在区间(10,10.2)内的袋数,则X的数学期望约为( )
注:若Z~N(μ,σ2),则P(μ-σ
4.若不等式|x-1|+|x+m|≤4的解集非空,则实数m的取值范围是( )
A.[-5,-3] B.[-3,5] C.[-5,3] D.[3,5]
5.某次联欢会要安排3个歌舞类节目, 2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )
A.72 B.120 C.144 D.168
6.由曲线y=,直线y=x﹣2及y轴所围成的图形的面积为( )
A. B.4 C. D.6
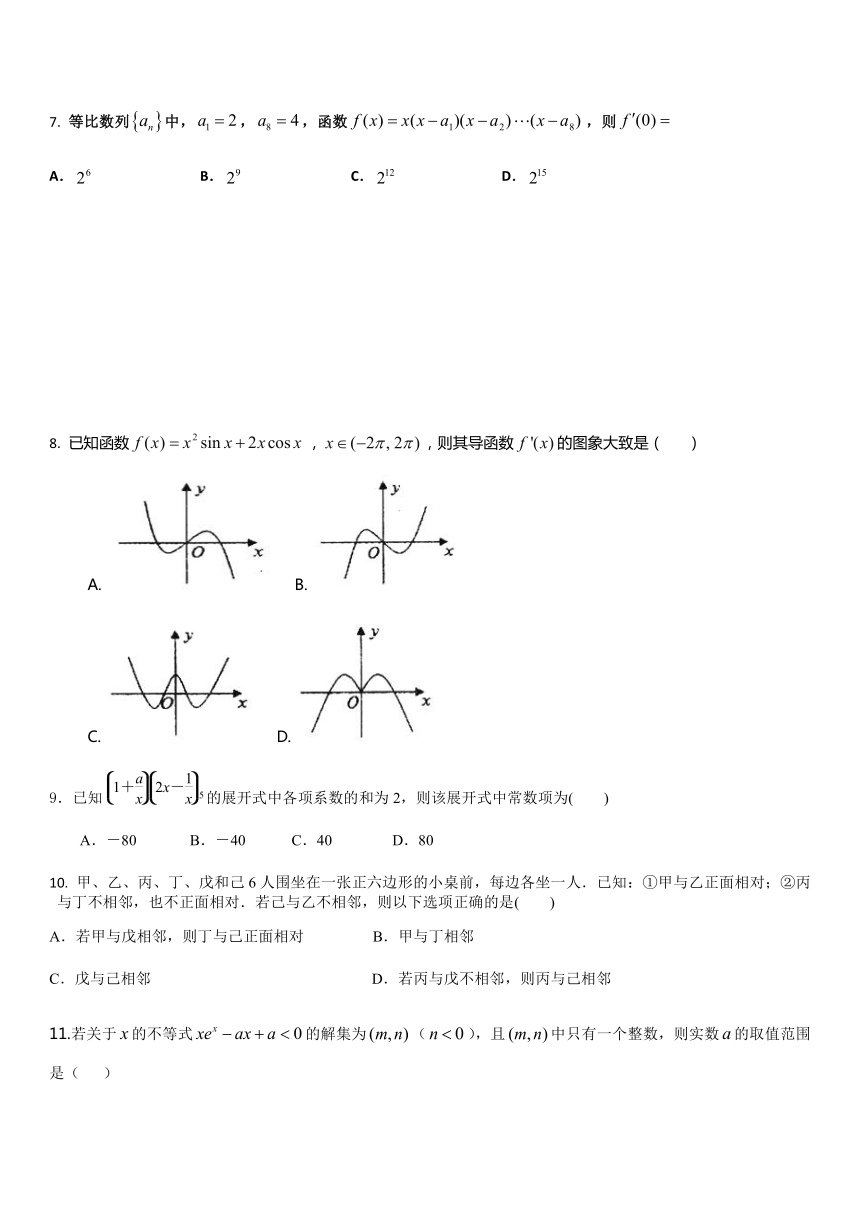
7. 等比数列中,,,函数,则
A. B. C. D.
8. 已知函数,,则其导函数的图象大致是( )
A. B.
C. D.
9.已知5的展开式中各项系数的和为2,则该展开式中常数项为( )
A.-80 B.-40 C.40 D.80
10. 甲、乙、丙、丁、戊和己6人围坐在一张正六边形的小桌前,每边各坐一人.已知:①甲与乙正面相对;②丙与丁不相邻,也不正面相对.若己与乙不相邻,则以下选项正确的是( )
A.若甲与戊相邻,则丁与己正面相对 B.甲与丁相邻
C.戊与己相邻 D.若丙与戊不相邻,则丙与己相邻
11.若关于的不等式的解集为(),且中只有一个整数,则实数的取值范围是( )
A. B. C. D.
12.定义在上的函数的导函数为,若,且,则( )
A. B. C. D.
二、填空题(共4小题,每小题5分,满分20分)
13.抛掷一个骰子,若掷出5点或6点就说试验成功,则在3次试验中恰有2次成功的概
率为__________.
14.观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律,第n个等式为 .
15.随机变量的取值为0,1,2,若,,则=________.
16.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是 (写出所有正确结论的编号).
①; ②; ③事件B与事件A1相互独立;
④A1,A2,A3是两两互斥的事件;
⑤P(B)的值不能确定,因为它与A1,A2,A3中哪一个发生都有关.
三、解答题(共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系中,直线:,圆:,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系.
(Ⅰ)求,的极坐标方程;(Ⅱ)若直线的极坐标方程为,设与的交点为, ,求的面积
18.(本题满分12分)有一款击鼓小游戏规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得50分,没有出现音乐则扣除150分(即获得-150分).设每次击鼓出现音乐的概率为,且各次击鼓是否出现音乐相互独立.
(1)玩一盘游戏,求至少出现一次音乐的概率;
(2)设每盘游戏获得的分数为X,求X的分布列;
(3)许多玩过这款游戏的人都发现,玩的盘数越多,分数没有增加反而减少了.请运用概率统计的相关知识分析其中的道理.
19.(本题满分12分)A市积极倡导学生参与绿色环保活动,其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月(一年)内空气质量指数进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API [0,50] (50,100] (100,150] (150,200] (200,250] (250,300] >300
空气质量 优 良 轻微污染 轻度污染 Ziyuanku.com中度污染 中重度污染 重度污染
天数 Ziyuanku.com4 13 18 30 9 11 15
(1)若A市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数(记为t)的关系
为:,在这一年内随机抽取一天,估计该天经济损失元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成列联表,并判断是否有的把握认为A市本年度空气重度污染与供暖有关?
非重度污染 重度污染 合计
供暖季
非供暖季节
合计 100
下面临界值表供参考.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 中anku.com3.841 www.ziyuanku.com5.024 6.635 7.879 10.828
参考公式:.
20. (本小题满分12分) “既要金山银山,又要绿水青山”。某风景区在一个直径为米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点(与不重合),沿修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。
(1)设(弧度),将绿化带的总长度表示为的函数;
(2)求绿化带的总长度的最大值。
21.(本小题满分12分)
设圆的圆心为,直线过点且与轴不重合,交圆于,两点,过作的平行线交于点.
(I)证明为定值,并写出点的轨迹方程;
(II)设点的轨迹为曲线,直线交于两点,过且与垂直的直线与圆交于两点,求四边形面积的取值范围.
22.(本小题满分12分)已知函数.
(Ⅰ) 求函数的单调区间和极值;
(Ⅱ)已知函数的图象与函数的图象关于直线对称.证明当时,;
(Ⅲ)如果且证明.
高二数学下学期质量检测四(理数)参考答案
一、CCBCB CCCDD DC
二、13. 14. n+(n+1)+(n+2)+…+(3n﹣2)=(2n﹣1)2 15. ;16.②④
三、计算题
17. 解:
(Ⅰ)因为,所以的极坐标方程为,的极坐标方程为……………………………5分
(Ⅱ)将代入,得,解得,故,即
由于的半径为1,所以的面积为………………………10分
18. (1)每盘游戏都需要击鼓三次,每次击鼓出现音乐的概率为,且各次击鼓出现音乐相互独立,∴玩一盘游戏,至少出现一次音乐的概率是p=1-3=.
(2)设每盘游戏获得的分数为X,则X可能取值为-150,10,20,50,
P(X=-150)=C03=,
P(X=10)=C2=,
P(X=20)=C2=,
P(X=50)=C3=.
∴X的分布列为
X -150 10 20 50
P
(3)由(2)得E(X)=-150×+10×+20×+50×=-,
∴每盘游戏得分的平均数是-,得负分.
∴玩的盘数越多,分数没有增加反而减少了.
19、(1)P(A)=;(2)95%的把握认为A市本年度空气重度污染与供暖有关.
【解析】
(1)设“在本年内随机抽取一天,该天经济损失P∈(200,600]元”为事件A
由200<4t﹣400≤600,得150<t≤250,频数为39,
∴P(A)=
(2)根据以上数据得到如表:
非重度污染 重度污染 合计
供暖季 22 8 30
非供暖季 63 7 70
合计 85 15 100
K2的观测值K2=≈4.575>3.841
所以有95%的把握认为A市本年度空气重度污染与供暖有关.
考点:分段函数、频率分布表、古典概型、独立性检验.
20. (1)设圆心为,连结。
在直角中,,弧的长;
所以,其中。
(2),,
令,可得,所以。
当时,,单调递增;
当时,,单调递减;
所以。
所以绿化带的总长度的最大值为米。
21.解:(Ⅰ)因为,,故,
所以,故.
又圆的标准方程为,从而,所以.
由题设得,,,由椭圆定义可得点的轨迹方程为:
().
(Ⅱ)当与轴不垂直时,设的方程为,,.
由得.
则,.
所以.
过点且与垂直的直线:,到的距离为,所以
.故四边形的面积
.
可得当与轴不垂直时,四边形面积的取值范围为.
当与轴垂直时,其方程为,,,四边形的面积为12.
综上,四边形面积的取值范围为.
22. 解:(Ⅰ)解:
令,解得x=1
当x变化时,,的变化情况如下表
X () 1 ()
+ 0 -
极大值
所以在()内是增函数,在()内是减函数.
函数在x=1处取得极大值f(1)且f(1)=
(Ⅱ)证明:由题意可知g(x)=f(2-x),得g(x)=(2-x)
令F(x)=f(x)-g(x),即
(Ⅲ)证明:(1)
若,由(Ⅰ)及,得与矛盾
(2)若,由(Ⅰ)及,得与矛盾
根据(1)(2)得
由(Ⅱ)可知,>,则=,所以>,从而>.因为,所以,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内是增函数,所以>,即>2.
同课章节目录
