7.3 第2课时 解复杂的一元一次不等式组课件(21张ppt)
文档属性
| 名称 | 7.3 第2课时 解复杂的一元一次不等式组课件(21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 868.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 10:29:28 | ||
图片预览








文档简介
(共21张PPT)
7.3 一元一次不等式组
第7章 一元一次不等式与
不等式组
导入新课
讲授新课
当堂练习
课堂小结
第2课时 解复杂的一元一次不等式组
七年级数学下(HK)
教学课件
1.会解复杂的一元一次不等式组,并会在数轴上表
示出来;(重点)
2.会通过列一元一次不等式组去解决生活中的实际
问题.(重点、难点)
学习目标
问题1 什么叫做不等式组的解集?
问题2 解一元一次不等式组的步骤是什么?
(1)分别求出每个不等式的解集;
不等式组中所有不等式的解集的公共部分,
叫做这个不等式组的解集.
导入新课
复习引入
交流:
说一说不等式的解集有哪几种情况?
2.假设a讲授新课
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
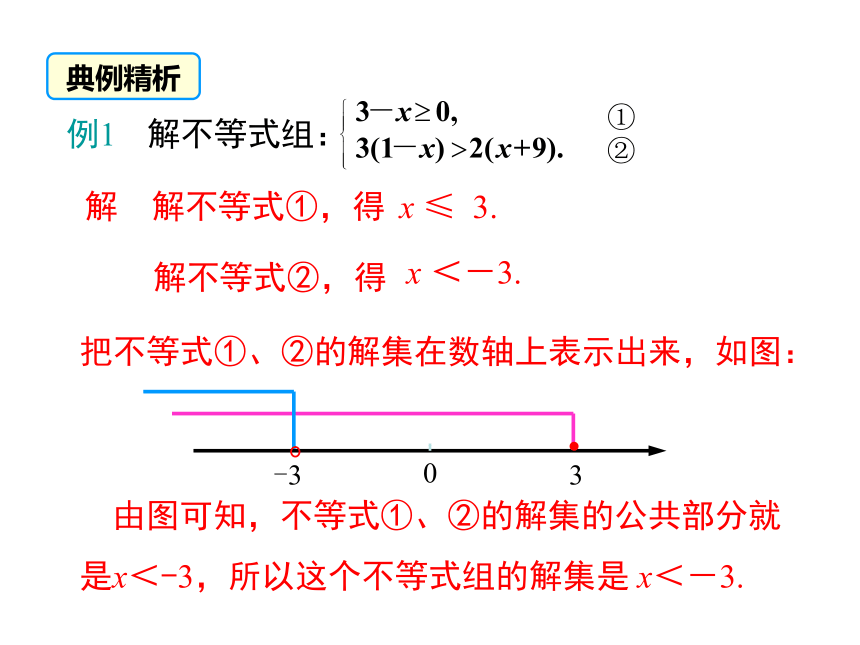
解不等式②,得
x <-3.
例1 解不等式组:
解 解不等式①,得
x ≤ 3.
把不等式①、②的解集在数轴上表示出来,如图:
由图可知,不等式①、②的解集的公共部分就
是x<-3,所以这个不等式组的解集是 x<-3.
典例精析
例2 解不等式组:
解 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3
练习:已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
解: 由不等式组得:
因为不等式组的解集为: -1< x < 1 ,
解得 a=1 , b= - 2
所以 (a+1)(b-1)=2×(-3)=-6.
问题 3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
解 设每个小组原先每天生产x件产品,由题意,得
解不等式组,得 .
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
总结归纳
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例4 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
D
解析:解第一个不等式得x≥-a,解第二个不等
式得x<1.因为不等式组无解,故-a≥1,
解得a≤-1.故选D.
当堂练习
2.某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若设该校计划每月烧煤 x t,求x的取值范围.
解:根据题意,得
4(x+5)>100, ①
4(x-5)<68. ②
解不等式②,得
x <22.
解不等式①,得
x >20.
因此,原不等式组的解集为 20<x <22.
3.有若干学生参加夏令营活动,晚上在一宾馆住宿
时,如果每间住4个,那么还有20人住不下,相同
的房间,如果每间住8人,那么还有一间住不满也
不空,请问:这群学生有多少人?有多少房间供
他们住?
解 设有x间房供他们住,则学生有(4x+20)人,
由题意,得
解不等式组,得5根据题意,x的值应是整数,所以x=6.
4x+20=44人.
答:有学生44人,有6间房供他们住.
一元一次不等式组
课堂小结
7.3 一元一次不等式组
第7章 一元一次不等式与
不等式组
导入新课
讲授新课
当堂练习
课堂小结
第2课时 解复杂的一元一次不等式组
七年级数学下(HK)
教学课件
1.会解复杂的一元一次不等式组,并会在数轴上表
示出来;(重点)
2.会通过列一元一次不等式组去解决生活中的实际
问题.(重点、难点)
学习目标
问题1 什么叫做不等式组的解集?
问题2 解一元一次不等式组的步骤是什么?
(1)分别求出每个不等式的解集;
不等式组中所有不等式的解集的公共部分,
叫做这个不等式组的解集.
导入新课
复习引入
交流:
说一说不等式的解集有哪几种情况?
2.假设a讲授新课
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
x
解不等式②,得
x <-3.
例1 解不等式组:
解 解不等式①,得
x ≤ 3.
把不等式①、②的解集在数轴上表示出来,如图:
由图可知,不等式①、②的解集的公共部分就
是x<-3,所以这个不等式组的解集是 x<-3.
典例精析
例2 解不等式组:
解 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3
练习:已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
解: 由不等式组得:
因为不等式组的解集为: -1< x < 1 ,
解得 a=1 , b= - 2
所以 (a+1)(b-1)=2×(-3)=-6.
问题 3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
解 设每个小组原先每天生产x件产品,由题意,得
解不等式组,得 .
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
总结归纳
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例4 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
D
解析:解第一个不等式得x≥-a,解第二个不等
式得x<1.因为不等式组无解,故-a≥1,
解得a≤-1.故选D.
当堂练习
2.某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若设该校计划每月烧煤 x t,求x的取值范围.
解:根据题意,得
4(x+5)>100, ①
4(x-5)<68. ②
解不等式②,得
x <22.
解不等式①,得
x >20.
因此,原不等式组的解集为 20<x <22.
3.有若干学生参加夏令营活动,晚上在一宾馆住宿
时,如果每间住4个,那么还有20人住不下,相同
的房间,如果每间住8人,那么还有一间住不满也
不空,请问:这群学生有多少人?有多少房间供
他们住?
解 设有x间房供他们住,则学生有(4x+20)人,
由题意,得
解不等式组,得5
4x+20=44人.
答:有学生44人,有6间房供他们住.
一元一次不等式组
课堂小结
