高中物理选修3-2 第四章电磁感应第6节 动生现象分析 (51张ppt)
文档属性
| 名称 | 高中物理选修3-2 第四章电磁感应第6节 动生现象分析 (51张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-15 13:20:24 | ||
图片预览




文档简介
(共51张PPT)
选修3-2 电磁感应
第6节 动生现象分析
温故
感生电动势:由于外加磁场改变而产生的感应电动势。
动生电动势:由于导体运动产生的感应电动势。
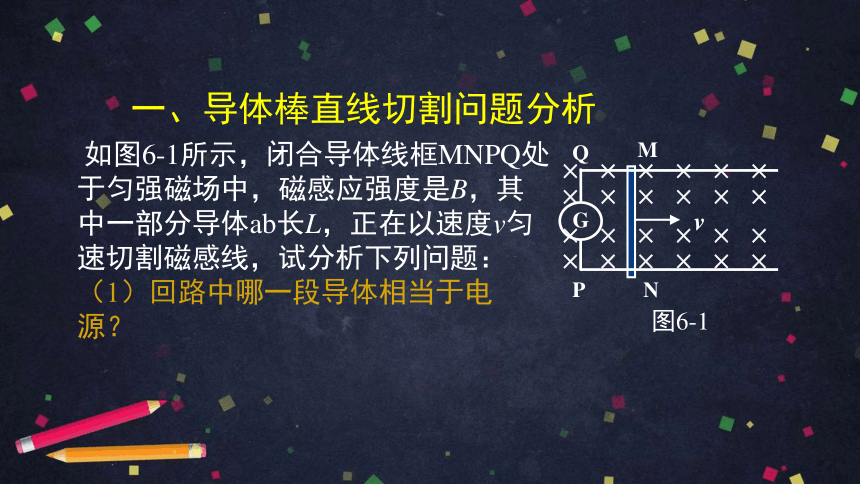
一、导体棒直线切割问题分析
如图6-1所示,闭合导体线框MNPQ处于匀强磁场中,磁感应强度是B,其中一部分导体ab长L,正在以速度v匀速切割磁感线,试分析下列问题:
(1)回路中哪一段导体相当于电源?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
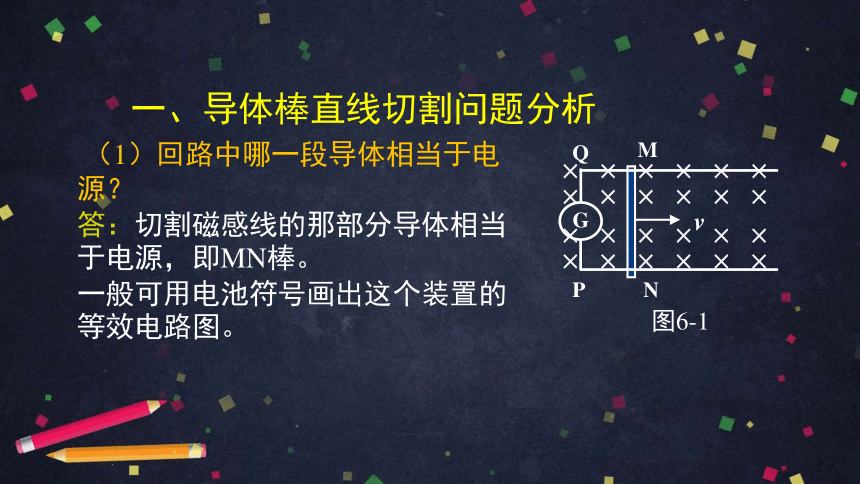
一、导体棒直线切割问题分析
(1)回路中哪一段导体相当于电源?
答:切割磁感线的那部分导体相当于电源,即MN棒。
一般可用电池符号画出这个装置的等效电路图。
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
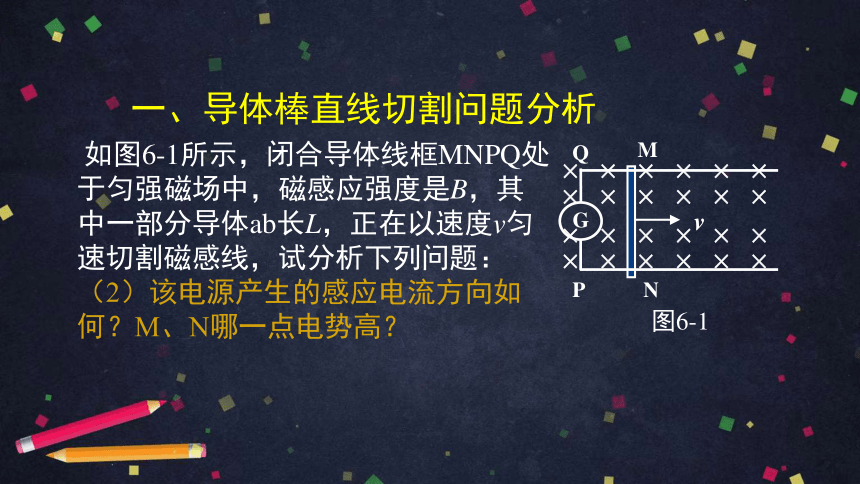
一、导体棒直线切割问题分析
如图6-1所示,闭合导体线框MNPQ处于匀强磁场中,磁感应强度是B,其中一部分导体ab长L,正在以速度v匀速切割磁感线,试分析下列问题:
(2)该电源产生的感应电流方向如何?M、N哪一点电势高?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
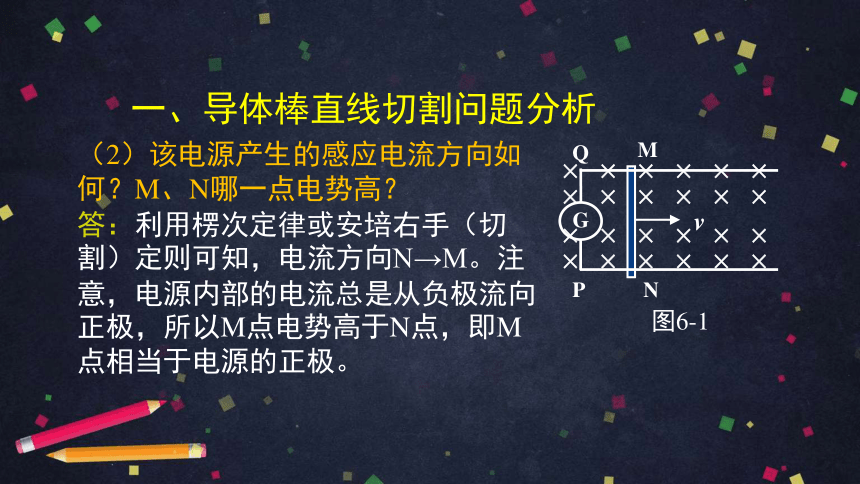
一、导体棒直线切割问题分析
(2)该电源产生的感应电流方向如何?M、N哪一点电势高?
答:利用楞次定律或安培右手(切割)定则可知,电流方向N→M。注意,电源内部的电流总是从负极流向正极,所以M点电势高于N点,即M点相当于电源的正极。
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
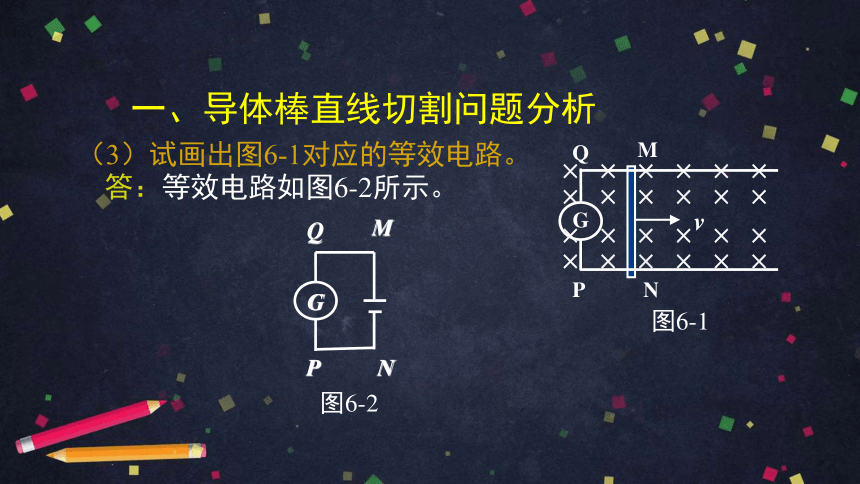
(3)试画出图6-1对应的等效电路。
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
G
M
N
P
Q
图6-2
答:等效电路如图6-2所示。
一、导体棒直线切割问题分析
如图6-1所示,闭合导体线框MNPQ处于匀强磁场中,磁感应强度是B,其中一部分导体ab长L,正在以速度v匀速切割磁感线,试分析下列问题:
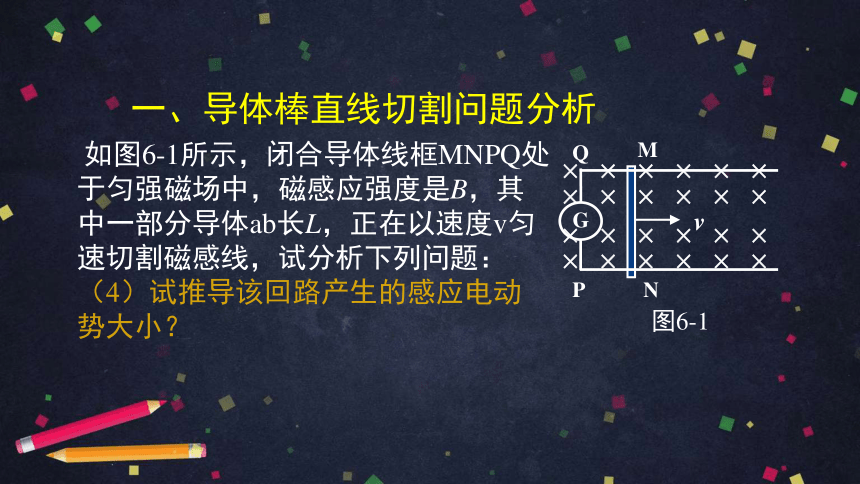
(4)试推导该回路产生的感应电动势大小?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
(4)试推导该回路产生的感应电动势大小?
答:有效面积的增加量:?S=L?v?t
磁通量的增加量:??=B??S
代入E感=N ??/?t
可得:
整理得:
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
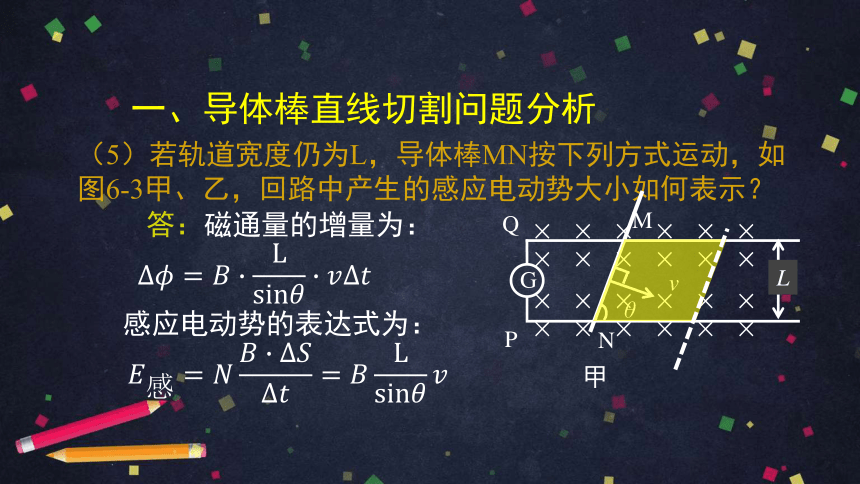
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
甲 乙
图6-3
× × × × × × × × × × × ×
× × × × × × × × × × × ×
M
N
θ
v
L
G
P
Q
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
答:磁通量的增量为:
感应电动势的表达式为:
一、导体棒直线切割问题分析
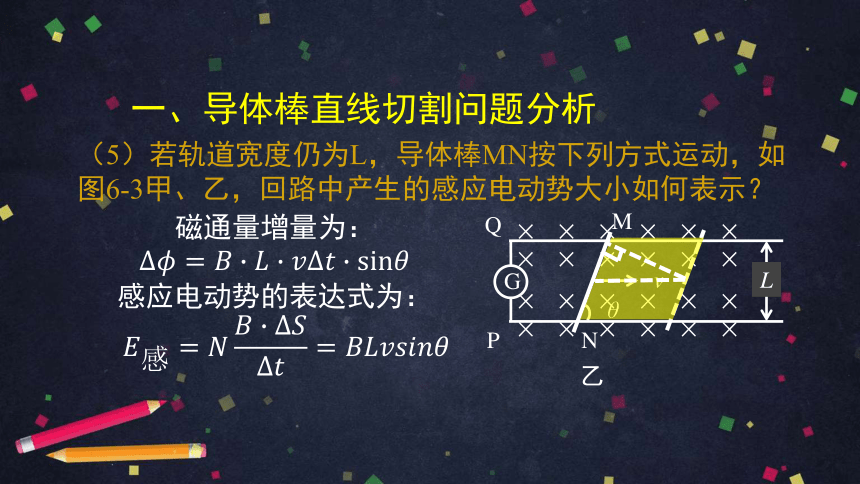
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
甲
× × × × × × × × × × × ×
× × × × × × × × × × × ×
M
N
θ
v
L
G
P
Q
一、导体棒直线切割问题分析
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
乙
磁通量增量为:
感应电动势的表达式为:
一、导体棒直线切割问题分析
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
感应电动势的表达式为:
令
动生电动势的公式可简写为:
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
乙
一、导体棒直线切割问题分析
研究表明,无论切割磁感线的导体棒形状如何,都可等效为如图6-5中丁图的形式。
v
?
v
v
v
?
L
M
N
甲 乙 丙 丁
图6-5
一、导体棒直线切割问题分析
(6)请问第(5)问中所说两种情况下,导体棒MN所受安培力方向如何?
甲 乙
图6-3
× × × × × × × × × × × ×
× × × × × × × × × × × ×
M
N
θ
v
L
G
P
Q
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
一、导体棒直线切割问题分析
例1.如图6-7所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻不计,在M和P之间接有R=3.0Ω的定值电阻,质量m=0.01kg导体棒长ab=0.5m,其电阻为r=1.0Ω,与导轨接触良好。整个装置处于方向竖直向下的匀强磁场中,B=0.4T。使ab在恒定外力F作用下从静止开始运动,最终导体棒以v=10m/s的速度向右做匀速运动。试分析以下问题:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(1)闭合导体回路中,哪一段导体相当于电源?其正负极分别是哪一端?
答: 闭合导体回路中,ab段导体相当于电源,a端为正极,b端为负极。
等效电路图如图6-8所示:
图6-7
R
B
r
P
M
N
a
Q
b
v
R
r
P
M
a
b
图6-8
一、导体棒直线切割问题分析
(2)稳定后闭合导体回路中的电流多少?
解得:
由闭合电路欧姆定律得:
解得:
R
r
P
M
a
b
图6-8
一、导体棒直线切割问题分析
(3)稳定后ab两点间的电压多少?
由欧姆定律得:
解得:
R
r
P
M
a
b
图6-8
一、导体棒直线切割问题分析
(4)稳定后维持ab做匀速运动的外力多少?
ab做匀速运动
F=F安
解得:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(5)稳定后外力做功的功率是多少?
解得:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(6)稳定后ab向右运动1m的过程中,外力做的功是多少?
解得:J
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(7)稳定后回路中产生的热量Q1是多少?
回路中产生的热量:
其中:
解得:J
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(8)试分析说明导体棒从静止到达到匀速运动之前的运动规律?
由牛顿第二定律:
由电磁感应规律:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(8)试分析说明导体棒从静止到达到匀速运动之前的运动规律?
整理得:
可见:导体棒ab将做加速度减小的变加速运动,直到a=0时,导体棒速度达到最大。
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(9)撤去外力后,回路中还能产生多少焦耳热Q2?
利用动能定理:
所以,焦耳热:
图6-7
R
B
r
P
M
N
a
Q
b
v
二、动生电动势与洛伦兹力的关系
为了研究方便,我们假定导体回路中自由移动的电荷带正电。
(1)试画出图6-1情景中导体棒内自由电荷相对于屏幕运动的大致方向?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
图6-9
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
图6-10
× × × ×
× × × ×
× × × ×
× × × ×
M
N
v
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
图6-11
× × × ×
× × × ×
× × × ×
× × × ×
M
N
v
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
图6-12
× × × ×
× × × ×
× × × ×
× × × ×
M
N
v
× × × ×
× × × ×
× × × ×
× × × ×
由平衡方程可得:
整理可得:
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
当导体棒MN没有对外供电时,其两端电势差就等于电源电动势,
若导体棒对外供电了,则U为电源的路端电压。
由平衡方程可得:
整理可得:
二、动生电动势与洛伦兹力的关系
动生电动势的产生微观上源于洛伦兹力作用。
三、导体棒转动切割磁感线问题分析
如图6-13所示,长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度ω匀速转动,磁场的磁感应强度为B,求杆OA杆产生的感应电动势大小,并判断O、A两点电势的高低。
图6-13
ω
A
O
三、导体棒转动切割磁感线问题分析
1.从法拉第电磁感应定律的角度:
由法拉第电磁感应定律:
图6-14
ω
A
O
A'
三、导体棒转动切割磁感线问题分析
2.从动生电动势的角度:
等效切割
导体棒OA上的感应电动势:
图6-14
ω
A
O
A'
三、导体棒转动切割磁感线问题分析
动生电动势方向的判定:
1.右手切割定则
2.洛伦兹力
图6-14
ω
A
O
v
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
区别1 求平均感应电动势。
E与某段时间或某个过程相对应。 求瞬时感应电动势。
E与某个时刻或某个位置相对应。
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
区别2 求的是整个电路的感应电动势。整个电路的感应电动势为零时,某段导体的感应电动势不一定为零。 求的是电路中的一部分导体切割磁感线时产生的感应电动势。
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
区别3 由于是整个电路的感应电动势,因此电源部分不容易确定。 由于是由一部分导体切割磁感线的运动产生的,该部分导体就相当于电源。
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
联系
三、导体棒转动切割磁感线问题分析
例2.一直升飞机停在北半球的地磁极上空,该处地磁场的方向竖直向下,磁感应强度为B,直升飞机螺旋桨叶片的长度为l,螺旋桨转动的频率为f,顺着地磁场的方向看螺旋桨,螺旋桨按顺时针方向转动.螺旋桨叶片的近轴端为a,远轴端为b,如图6-15所示.如果忽略a到转轴中心线的距离,用E表示每个叶片中的感应电动势,则 ( )
图6-15
三、导体棒转动切割磁感线问题分析
例2.用E表示每个叶片中的感应电动势,则 ( )
A.,且a点电势低于b点电势
B.,且a点电势低于b点电势
C.,且a点电势高于b点电势
D.,且a点电势高于b点电势
图6-15
三、导体棒转动切割磁感线问题分析
例2.用E表示每个叶片中的感应电动势,则 ( )
A.,且a点电势低于b点电势
B.,且a点电势低于b点电势
C.,且a点电势高于b点电势
D.,且a点电势高于b点电势
图6-16
b
a
ω=
三、导体棒转动切割磁感线问题分析
例3.如图6-17所示,竖直平面内有一金属圆环,半径为a,总电阻为指剪开拉直时的电阻,磁感应强度为B的匀强磁场垂直穿过环平面。环的最高点A用铰链连接长度为2a、电阻为的导体棒AB,AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,试分析:
(1)从微观角度分析说明导体棒A、B端电势高低?
B
O
A
B
图6-17
三、导体棒转动切割磁感线问题分析
例3.(1)从微观角度分析说明导体棒A、B端电势高低?
答:从微观上看,当导体棒运动到竖直位置时,导体棒内所有自由电子都有一个随棒向左运动的速度,由左手定则可知,此时自由电子收到洛伦兹力方向均沿导体棒指向A端,所以A端会聚集大量负电荷,导致B端多出大量正电荷,由此可以判知,A端电势低,B端电势高。
B
O
A
B
图6-17
三、导体棒转动切割磁感线问题分析
例3.(1)从微观角度分析说明导体棒A、B端电势高低?
答:从微观上看,当导体棒运动到竖直位置时,导体棒内所有自由电子都有一个随棒向左运动的速度,由左手定则可知,此时自由电子收到洛伦兹力方向均沿导体棒指向A端,所以A端会聚集大量负电荷,导致B端多出大量正电荷,由此可以判知,A端电势低,B端电势高。
A
图6-18
B
三、导体棒转动切割磁感线问题分析
例3.如图6-17所示,竖直平面内有一金属圆环,半径为a,总电阻为指剪开拉直时的电阻,磁感应强度为B的匀强磁场垂直穿过环平面。环的最高点A用铰链连接长度为2a、电阻为的导体棒AB,AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,试分析:
(2)这时AB两端的电压大小为多少?
B
O
A
B
图6-17
三、导体棒转动切割磁感线问题分析
例3.
(2)这时AB两端的电压大小为多少?
答:当摆到竖直位置时,导体棒产生的感应电动势为:
金属环并联的电阻为:
图6-18
B
三、导体棒转动切割磁感线问题分析
例3.
(2)这时AB两端的电压大小为多少?
答:
AB两端的电压是路端电压,AB两端的电压大小为:
图6-18
B
本课小结
1.研究了常见动生电动势的基本问题。
2.从微观上分析了动生电动势与洛伦兹力的关系。
3.学习使用单棒切割磁感线时动生电动势表达式。
谢谢观看!
选修3-2 电磁感应
第6节 动生现象分析
温故
感生电动势:由于外加磁场改变而产生的感应电动势。
动生电动势:由于导体运动产生的感应电动势。
一、导体棒直线切割问题分析
如图6-1所示,闭合导体线框MNPQ处于匀强磁场中,磁感应强度是B,其中一部分导体ab长L,正在以速度v匀速切割磁感线,试分析下列问题:
(1)回路中哪一段导体相当于电源?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
(1)回路中哪一段导体相当于电源?
答:切割磁感线的那部分导体相当于电源,即MN棒。
一般可用电池符号画出这个装置的等效电路图。
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
如图6-1所示,闭合导体线框MNPQ处于匀强磁场中,磁感应强度是B,其中一部分导体ab长L,正在以速度v匀速切割磁感线,试分析下列问题:
(2)该电源产生的感应电流方向如何?M、N哪一点电势高?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
(2)该电源产生的感应电流方向如何?M、N哪一点电势高?
答:利用楞次定律或安培右手(切割)定则可知,电流方向N→M。注意,电源内部的电流总是从负极流向正极,所以M点电势高于N点,即M点相当于电源的正极。
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
(3)试画出图6-1对应的等效电路。
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
G
M
N
P
Q
图6-2
答:等效电路如图6-2所示。
一、导体棒直线切割问题分析
如图6-1所示,闭合导体线框MNPQ处于匀强磁场中,磁感应强度是B,其中一部分导体ab长L,正在以速度v匀速切割磁感线,试分析下列问题:
(4)试推导该回路产生的感应电动势大小?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
(4)试推导该回路产生的感应电动势大小?
答:有效面积的增加量:?S=L?v?t
磁通量的增加量:??=B??S
代入E感=N ??/?t
可得:
整理得:
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
一、导体棒直线切割问题分析
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
甲 乙
图6-3
× × × × × × × × × × × ×
× × × × × × × × × × × ×
M
N
θ
v
L
G
P
Q
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
答:磁通量的增量为:
感应电动势的表达式为:
一、导体棒直线切割问题分析
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
甲
× × × × × × × × × × × ×
× × × × × × × × × × × ×
M
N
θ
v
L
G
P
Q
一、导体棒直线切割问题分析
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
乙
磁通量增量为:
感应电动势的表达式为:
一、导体棒直线切割问题分析
(5)若轨道宽度仍为L,导体棒MN按下列方式运动,如图6-3甲、乙,回路中产生的感应电动势大小如何表示?
感应电动势的表达式为:
令
动生电动势的公式可简写为:
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
乙
一、导体棒直线切割问题分析
研究表明,无论切割磁感线的导体棒形状如何,都可等效为如图6-5中丁图的形式。
v
?
v
v
v
?
L
M
N
甲 乙 丙 丁
图6-5
一、导体棒直线切割问题分析
(6)请问第(5)问中所说两种情况下,导体棒MN所受安培力方向如何?
甲 乙
图6-3
× × × × × × × × × × × ×
× × × × × × × × × × × ×
M
N
θ
v
L
G
P
Q
× × × × × × × × × × × ×
× × × × × × × × × × × ×
P
Q
M
N
θ
L
G
v
一、导体棒直线切割问题分析
例1.如图6-7所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻不计,在M和P之间接有R=3.0Ω的定值电阻,质量m=0.01kg导体棒长ab=0.5m,其电阻为r=1.0Ω,与导轨接触良好。整个装置处于方向竖直向下的匀强磁场中,B=0.4T。使ab在恒定外力F作用下从静止开始运动,最终导体棒以v=10m/s的速度向右做匀速运动。试分析以下问题:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(1)闭合导体回路中,哪一段导体相当于电源?其正负极分别是哪一端?
答: 闭合导体回路中,ab段导体相当于电源,a端为正极,b端为负极。
等效电路图如图6-8所示:
图6-7
R
B
r
P
M
N
a
Q
b
v
R
r
P
M
a
b
图6-8
一、导体棒直线切割问题分析
(2)稳定后闭合导体回路中的电流多少?
解得:
由闭合电路欧姆定律得:
解得:
R
r
P
M
a
b
图6-8
一、导体棒直线切割问题分析
(3)稳定后ab两点间的电压多少?
由欧姆定律得:
解得:
R
r
P
M
a
b
图6-8
一、导体棒直线切割问题分析
(4)稳定后维持ab做匀速运动的外力多少?
ab做匀速运动
F=F安
解得:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(5)稳定后外力做功的功率是多少?
解得:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(6)稳定后ab向右运动1m的过程中,外力做的功是多少?
解得:J
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(7)稳定后回路中产生的热量Q1是多少?
回路中产生的热量:
其中:
解得:J
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(8)试分析说明导体棒从静止到达到匀速运动之前的运动规律?
由牛顿第二定律:
由电磁感应规律:
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(8)试分析说明导体棒从静止到达到匀速运动之前的运动规律?
整理得:
可见:导体棒ab将做加速度减小的变加速运动,直到a=0时,导体棒速度达到最大。
图6-7
R
B
r
P
M
N
a
Q
b
v
一、导体棒直线切割问题分析
(9)撤去外力后,回路中还能产生多少焦耳热Q2?
利用动能定理:
所以,焦耳热:
图6-7
R
B
r
P
M
N
a
Q
b
v
二、动生电动势与洛伦兹力的关系
为了研究方便,我们假定导体回路中自由移动的电荷带正电。
(1)试画出图6-1情景中导体棒内自由电荷相对于屏幕运动的大致方向?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
图6-9
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
图6-10
× × × ×
× × × ×
× × × ×
× × × ×
M
N
v
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
M
N
v
P
Q
图6-1
图6-11
× × × ×
× × × ×
× × × ×
× × × ×
M
N
v
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
图6-12
× × × ×
× × × ×
× × × ×
× × × ×
M
N
v
× × × ×
× × × ×
× × × ×
× × × ×
由平衡方程可得:
整理可得:
二、动生电动势与洛伦兹力的关系
(2)上述回路中正电荷定向移动过程中所受洛伦兹力的方向?
当导体棒MN没有对外供电时,其两端电势差就等于电源电动势,
若导体棒对外供电了,则U为电源的路端电压。
由平衡方程可得:
整理可得:
二、动生电动势与洛伦兹力的关系
动生电动势的产生微观上源于洛伦兹力作用。
三、导体棒转动切割磁感线问题分析
如图6-13所示,长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度ω匀速转动,磁场的磁感应强度为B,求杆OA杆产生的感应电动势大小,并判断O、A两点电势的高低。
图6-13
ω
A
O
三、导体棒转动切割磁感线问题分析
1.从法拉第电磁感应定律的角度:
由法拉第电磁感应定律:
图6-14
ω
A
O
A'
三、导体棒转动切割磁感线问题分析
2.从动生电动势的角度:
等效切割
导体棒OA上的感应电动势:
图6-14
ω
A
O
A'
三、导体棒转动切割磁感线问题分析
动生电动势方向的判定:
1.右手切割定则
2.洛伦兹力
图6-14
ω
A
O
v
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
区别1 求平均感应电动势。
E与某段时间或某个过程相对应。 求瞬时感应电动势。
E与某个时刻或某个位置相对应。
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
区别2 求的是整个电路的感应电动势。整个电路的感应电动势为零时,某段导体的感应电动势不一定为零。 求的是电路中的一部分导体切割磁感线时产生的感应电动势。
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
区别3 由于是整个电路的感应电动势,因此电源部分不容易确定。 由于是由一部分导体切割磁感线的运动产生的,该部分导体就相当于电源。
三、导体棒转动切割磁感线问题分析
公式E=与E=Blv⊥的区别与联系
? E=Blv⊥
联系
三、导体棒转动切割磁感线问题分析
例2.一直升飞机停在北半球的地磁极上空,该处地磁场的方向竖直向下,磁感应强度为B,直升飞机螺旋桨叶片的长度为l,螺旋桨转动的频率为f,顺着地磁场的方向看螺旋桨,螺旋桨按顺时针方向转动.螺旋桨叶片的近轴端为a,远轴端为b,如图6-15所示.如果忽略a到转轴中心线的距离,用E表示每个叶片中的感应电动势,则 ( )
图6-15
三、导体棒转动切割磁感线问题分析
例2.用E表示每个叶片中的感应电动势,则 ( )
A.,且a点电势低于b点电势
B.,且a点电势低于b点电势
C.,且a点电势高于b点电势
D.,且a点电势高于b点电势
图6-15
三、导体棒转动切割磁感线问题分析
例2.用E表示每个叶片中的感应电动势,则 ( )
A.,且a点电势低于b点电势
B.,且a点电势低于b点电势
C.,且a点电势高于b点电势
D.,且a点电势高于b点电势
图6-16
b
a
ω=
三、导体棒转动切割磁感线问题分析
例3.如图6-17所示,竖直平面内有一金属圆环,半径为a,总电阻为指剪开拉直时的电阻,磁感应强度为B的匀强磁场垂直穿过环平面。环的最高点A用铰链连接长度为2a、电阻为的导体棒AB,AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,试分析:
(1)从微观角度分析说明导体棒A、B端电势高低?
B
O
A
B
图6-17
三、导体棒转动切割磁感线问题分析
例3.(1)从微观角度分析说明导体棒A、B端电势高低?
答:从微观上看,当导体棒运动到竖直位置时,导体棒内所有自由电子都有一个随棒向左运动的速度,由左手定则可知,此时自由电子收到洛伦兹力方向均沿导体棒指向A端,所以A端会聚集大量负电荷,导致B端多出大量正电荷,由此可以判知,A端电势低,B端电势高。
B
O
A
B
图6-17
三、导体棒转动切割磁感线问题分析
例3.(1)从微观角度分析说明导体棒A、B端电势高低?
答:从微观上看,当导体棒运动到竖直位置时,导体棒内所有自由电子都有一个随棒向左运动的速度,由左手定则可知,此时自由电子收到洛伦兹力方向均沿导体棒指向A端,所以A端会聚集大量负电荷,导致B端多出大量正电荷,由此可以判知,A端电势低,B端电势高。
A
图6-18
B
三、导体棒转动切割磁感线问题分析
例3.如图6-17所示,竖直平面内有一金属圆环,半径为a,总电阻为指剪开拉直时的电阻,磁感应强度为B的匀强磁场垂直穿过环平面。环的最高点A用铰链连接长度为2a、电阻为的导体棒AB,AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,试分析:
(2)这时AB两端的电压大小为多少?
B
O
A
B
图6-17
三、导体棒转动切割磁感线问题分析
例3.
(2)这时AB两端的电压大小为多少?
答:当摆到竖直位置时,导体棒产生的感应电动势为:
金属环并联的电阻为:
图6-18
B
三、导体棒转动切割磁感线问题分析
例3.
(2)这时AB两端的电压大小为多少?
答:
AB两端的电压是路端电压,AB两端的电压大小为:
图6-18
B
本课小结
1.研究了常见动生电动势的基本问题。
2.从微观上分析了动生电动势与洛伦兹力的关系。
3.学习使用单棒切割磁感线时动生电动势表达式。
谢谢观看!
