高中物理人教版必修1课后习题 第三章 4 力的合成 Word版含解析
文档属性
| 名称 | 高中物理人教版必修1课后习题 第三章 4 力的合成 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-15 13:42:48 | ||
图片预览

文档简介
1.下列物理量在运算时不遵循平行四边形定则的有( )
A.时间 B.位移 C.速度 D.加速度
解析时间是标量,位移、速度、加速度是矢量,矢量的运算遵循平行四边形定则,故选A。
答案A
2.(多选)关于大小不变的两个共点力F1、F2的合力F,下列说法正确的是( )
A.合力F的大小一定大于任一分力的大小
B.合力F的大小可能小于任一分力的大小
C.合力F的大小可能等于F1或F2的大小
D.合力F的大小随F1、F2间夹角增大而增大
解析由共点力合成的平行四边形定则可知,由于表示分力的两邻边的长短及其夹角的变化,使得表示合力的对角线的长度大于两邻边、小于两邻边、等于两邻边或其中某一邻边都是可能的,所以,合力的大小大于分力的大小、小于分力的大小、等于分力的大小也都是可能的。另外,平行四边形中两邻边夹角越小,其对角线越长;夹角越大,其对角线越短。所以,合力的大小随分力间夹角减小而增大,随分力间夹角增大而减小。正确选项为B、C。
答案BC
3.关于力F1、F2及它们的合力F的下列说法中,正确的是 ( )
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同种性质的力
C.两力F1、F2可能是同一个物体受到的力,也可能是物体间的相互作用力
D.两力F1、F2与F是物体同时受到的三个力
解析合力与分力产生的效果相同,故选项A正确;两个分力性质可以相同,也可以不同,故选项B错误;两个分力一定是作用在同一个物体上,故选项C错误;分力与合力作用效果相同,但不是同时作用在物体上的力,故选项D错误。
答案A
4.
如图所示,轻绳OA、OB和OP将一只元宵花灯悬挂在P点,花灯保持静止。已知绳OA和OB的夹角为120°,对O点拉力的大小皆为F,轻绳OP对O点拉力的大小为( )
A.F B.F C.F D.2F
解析轻绳OP对O点拉力的大小等于绳OA和OB的拉力的合力,根据几何知识可知,应为F。
答案A
5.两个共点力,一个力F1=40 N,另一个力为F2,它们的合力F=100 N,则F2的大小可能是( )
A.20 N B.40 N C.80 N D.160 N
解析F1和F2两个力的合力范围是|F1-F2|≤F≤F1+F2,判断可知选项C正确。
答案C
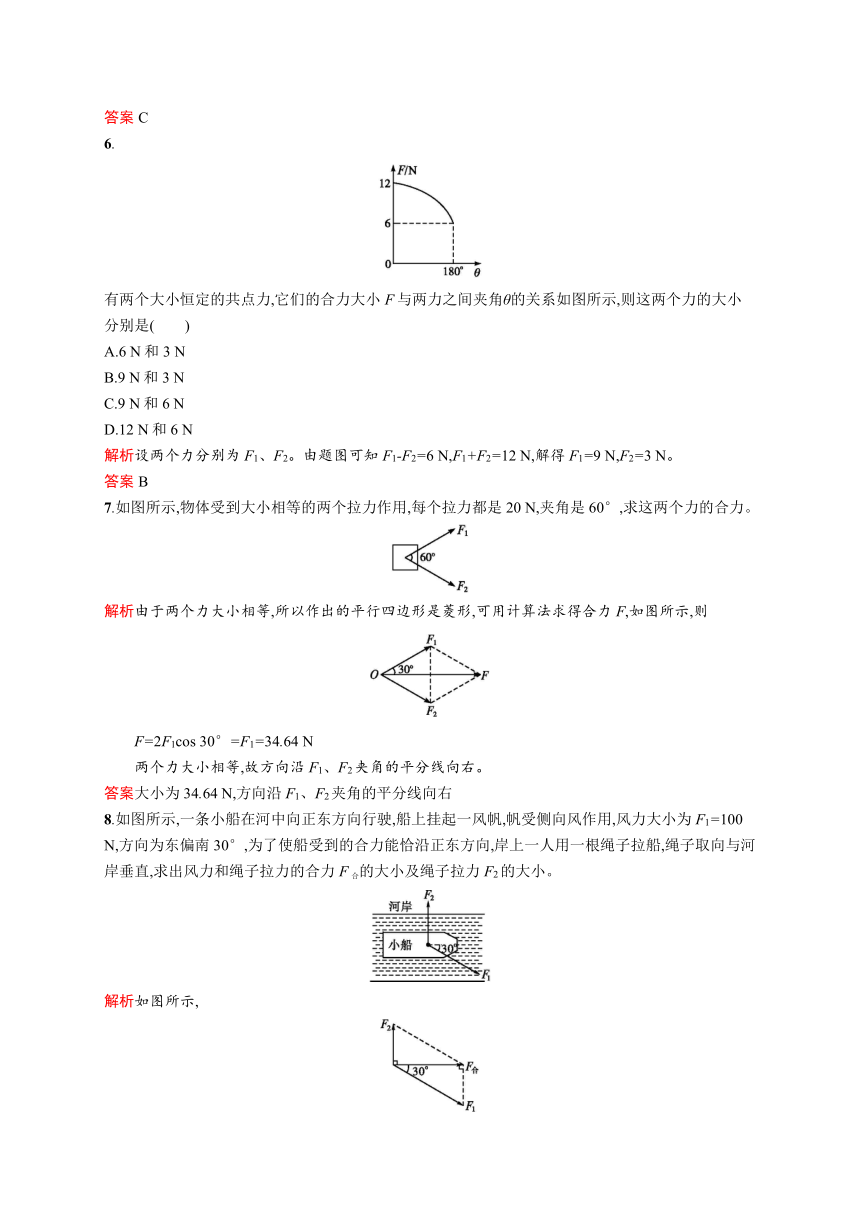
6.
有两个大小恒定的共点力,它们的合力大小F与两力之间夹角θ的关系如图所示,则这两个力的大小分别是( )
A.6 N和3 N
B.9 N和3 N
C.9 N和6 N
D.12 N和6 N
解析设两个力分别为F1、F2。由题图可知F1-F2=6 N,F1+F2=12 N,解得F1=9 N,F2=3 N。
答案B
7.如图所示,物体受到大小相等的两个拉力作用,每个拉力都是20 N,夹角是60°,求这两个力的合力。
解析由于两个力大小相等,所以作出的平行四边形是菱形,可用计算法求得合力F,如图所示,则
F=2F1cos 30°=F1=34.64 N
两个力大小相等,故方向沿F1、F2夹角的平分线向右。
答案大小为34.64 N,方向沿F1、F2夹角的平分线向右
8.如图所示,一条小船在河中向正东方向行驶,船上挂起一风帆,帆受侧向风作用,风力大小为F1=100 N,方向为东偏南30°,为了使船受到的合力能恰沿正东方向,岸上一人用一根绳子拉船,绳子取向与河岸垂直,求出风力和绳子拉力的合力F合的大小及绳子拉力F2的大小。
解析如图所示,
以F1、F2为邻边作平行四边形,使合力F沿正东方向,则
F合=F1cos 30°=100× N=50 N
F2=F1sin 30°=100× N=50 N。
答案50 N 50 N
能力提升
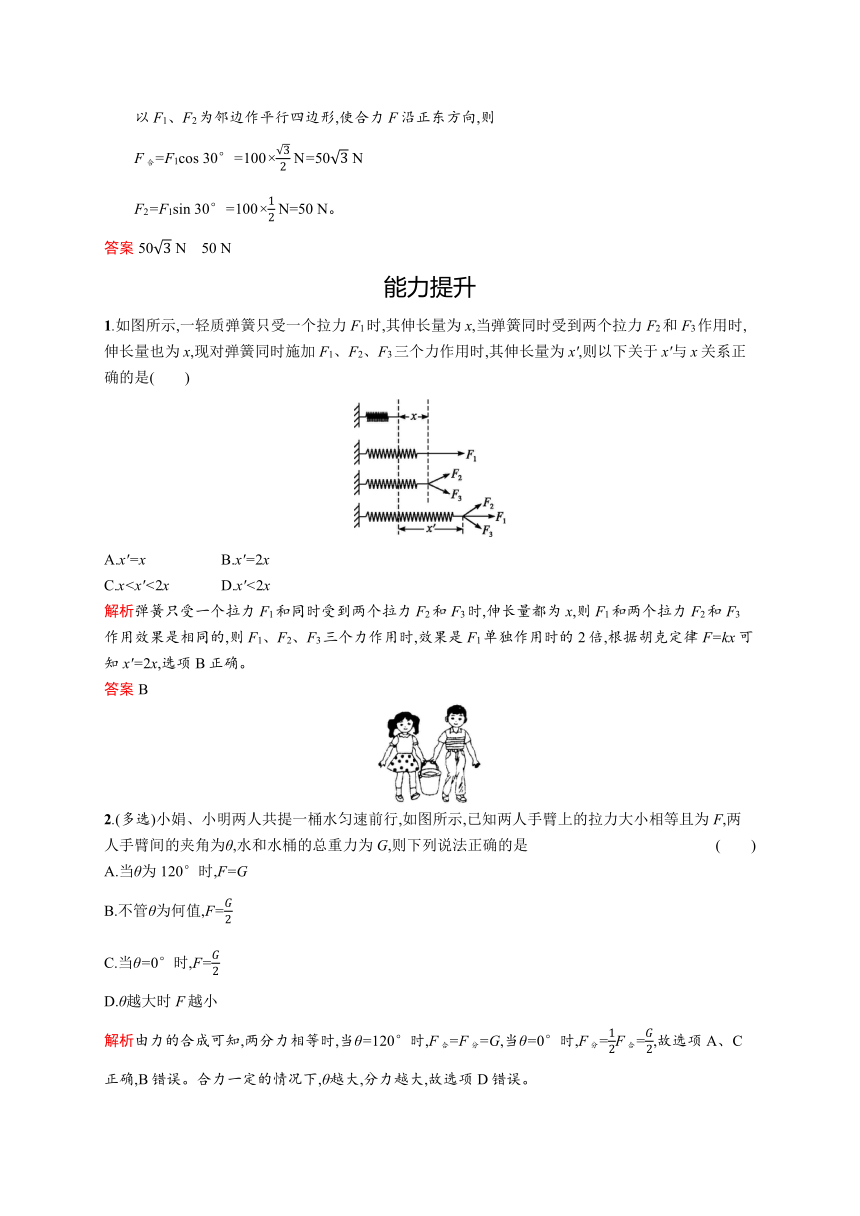
1.如图所示,一轻质弹簧只受一个拉力F1时,其伸长量为x,当弹簧同时受到两个拉力F2和F3作用时,伸长量也为x,现对弹簧同时施加F1、F2、F3三个力作用时,其伸长量为x',则以下关于x'与x关系正确的是( )
A.x'=x B.x'=2x
C.x
答案B
2.(多选)小娟、小明两人共提一桶水匀速前行,如图所示,已知两人手臂上的拉力大小相等且为F,两人手臂间的夹角为θ,水和水桶的总重力为G,则下列说法正确的是 ( )
A.当θ为120°时,F=G
B.不管θ为何值,F=
C.当θ=0°时,F=
D.θ越大时F越小
解析由力的合成可知,两分力相等时,当θ=120°时,F合=F分=G,当θ=0°时,F分=F合=,故选项A、C正确,B错误。合力一定的情况下,θ越大,分力越大,故选项D错误。
答案AC
3.(多选)两个共点力的合力为F,如果它们之间的夹角θ固定不变,而其中一个力增大,则( )
A.合力F一定增大
B.合力F的大小可能不变
C.合力F可能增大,也可能减小
D.当0°<θ<90°时,合力F一定减小
解析考虑到两个分力在一条直线上的情况,选项B正确,A错误;当0°<θ<90°时,一个力增大,则合力一定增大,选项D错误;考虑到两个分力夹角可能大于90°,也可能小于90°的情况,选项C正确。
答案BC
4.(多选)大小为4 N、7 N、9 N的三个共点力作用在一个物体上,则( )
A.物体所受的合力的最大值为20 N
B.三个力合力的最小值为2 N
C.三个力合力的最小值为零
D.三个力的合力可能是5 N
解析当三力同向时,合力最大为Fm=(4+7+9) N=20 N,选项A正确;4 N、7 N的合力范围为3~11 N,包含9 N,则这三个力合力的最小值为零,选项C正确;三个力合力的范围为0~20 N,即合力可能为5 N,选项D正确。
答案ACD
5.设有三个力同时作用在质点P上,它们的大小和方向相当于正六边形的两条边和一条对角线,如图所示,这三个力中最小的力的大小为F,则这三个力的合力等于 ( )
A.3F B.4F
C.5F D.6F
解析由几何关系得F3=2F,又F1、F2夹角为120°,大小均为F,故其合力大小为F,方向与F3相同,因此三个力的合力大小为3F,A正确。
答案A
6.(多选)骨折病人的牵引装置示意图如图所示,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内。为了使脚所受的拉力增大,可采取的方法是( )
A.只增加绳的长度
B.只增加重物的质量
C.只将病人的脚向左移动
D.只将两定滑轮的间距变大
解析
受力分析如图所示,由几何关系得F=2F1cos θ,若只增加绳的长度,F1、θ不变,则F不变,选项A错误;若只增加重物的质量,F1变大,则F变大,选项B正确;若只将病人的脚左移,θ变小,则F变大,选项C正确;若只将两定滑轮的间距变大,θ变大,则F变小,选项D错误。
答案BC
7.两个大小相等的共点力F1和F2,当它们的夹角为90°时,合力大小为F。当它们的夹角为60°时,合力为多大?
解析当F1和F2的夹角为90°时,
F=F1,即F1=F。
当F1和F2的夹角为60°时,作力的合成的平行四边形如图所示,
合力F'是平行四边形的对角线,则F'=2F1cos 30°=F。
答案F
8.
俯视图
如图所示,在水平地面上放一质量为1.0 kg的木块,木块与地面间的动摩擦因数为0.6,在水平方向上对木块同时施加相互垂直的两个拉力F1、F2,已知F1=3.0 N,F2=4.0 N,g取10 m/s2,则
木块受到的摩擦力为多少?若将F2顺时针转90°,此时木块在水平方向上受的合力大小为多少?
解析由平行四边形定则可知,题图中F1与F2的合力F==5.0 N。若木块滑动时,木块受到的滑动摩擦力大小为F'=μFN=μmg=6.0 N。由于F
答案5.0 N 1.0 N
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
