【备战2020】高考数学二轮专题:专题十一 高中数学填选题解题技巧 复习学案(上海地区专用)
文档属性
| 名称 | 【备战2020】高考数学二轮专题:专题十一 高中数学填选题解题技巧 复习学案(上海地区专用) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 15:33:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【备考2020】高考数学二轮专题复习学案
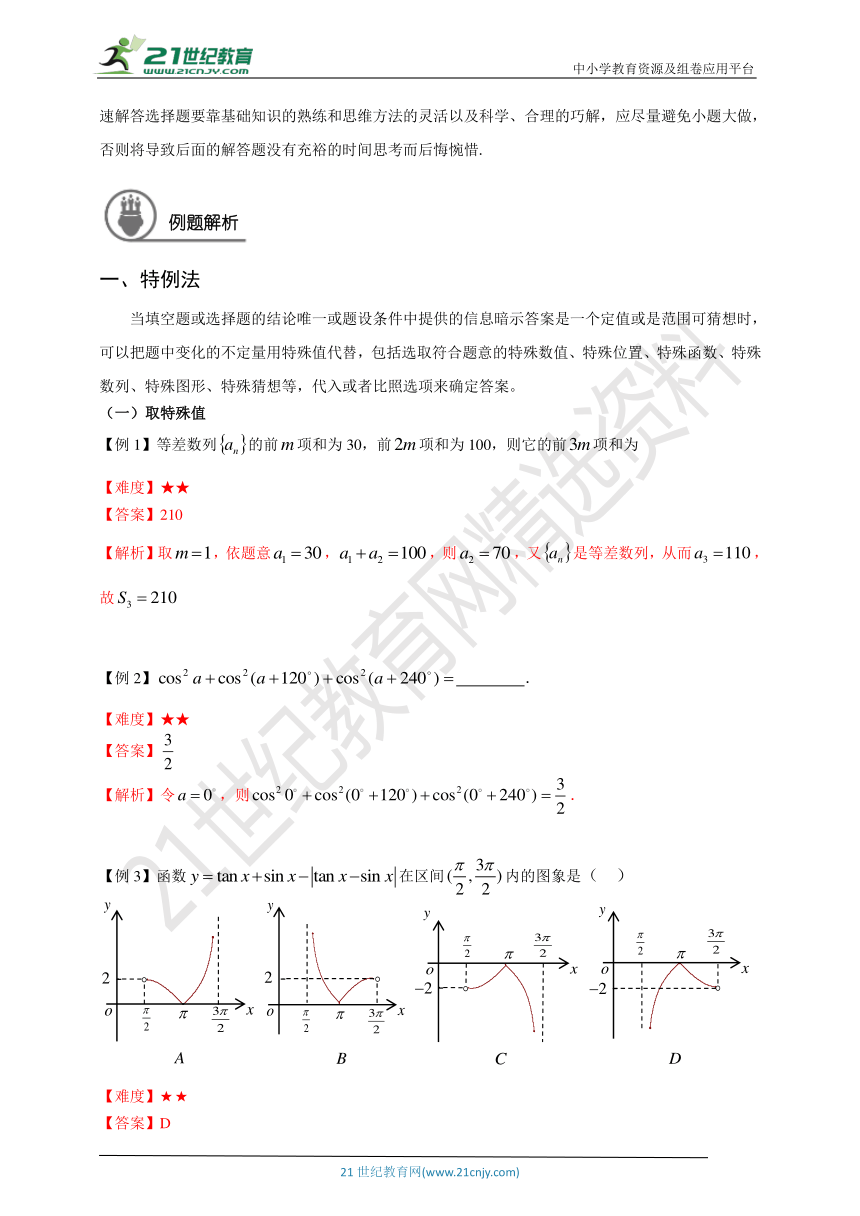
专题十一 高中数学填选题解题技巧
课题 高中数学填选题解题技巧 单元 第章 学科 数学 年级 十二
学习 目标 1.解填空题时,要有合理的分析和判断,要求推理、运算的每一步骤都正确无误,还要求将答案表达得准确、完整. 合情推理、优化思路、少算多思将是快速、准确地解答填空题的基本要求. 2.解选择题的常用方法,主要分直接法和间接法两大类.直接法是解答选择题最基本、最常用的方法;但高考的题量较大,如果所有选择题都用直接法解答,不但时间不允许,甚至有些题目根本无法解答.因此,我们还要掌握一些特殊的解答选择题的方法.
重点 让学生学会小题小做,争取巧做,尽力做到合理、正确、迅速。
难点 让学生学会小题小做,争取巧做,尽力做到合理、正确、迅速。
教学安排
版块 时长
1 知识梳理 30
2 例题解析 60
3 巩固训练 20
4 师生总结 10
5 课后练习 30
解答填空题的基本策略是“正确、合理、迅速”. 正确是解题的根本,由于填空题只填写最终结果,因而答案的正确显得尤为重要,因而解题时要思维缜密,步骤严谨,特别注意审题,清楚要求解的问题是什么,对答案中的细节要求要看清楚,如:“用数字作答”、“正确的是”、“不正确的是”、“写出所有真命题的代号”、“填上你认为正确的一个即可”、“不等式的解集是”等等,要按照要求答题;合理是正确的前提,运算过程合理,运算方法简便为运算结果的正确提供必要的保证;而迅速是建立在合理的基础上,要提高速度必须概念清楚、运算熟练以及科学、合理的巧解. 所以解题时要认真审题、弄清概念、明白算理、善于转化.
高考数学选择题的特点是:①提供了供选择的多个选择支(只有一个正确项);②不要求写出解答过程;③对解题速度有更高的要求. 所以解答选择题的基本策略是尽量“不择手段”的采用最简捷方法快速准确的作答,一是要充分挖掘各选择支的暗示作用,二是要巧妙有效的排除迷惑支的干扰. 快速解答选择题要靠基础知识的熟练和思维方法的灵活以及科学、合理的巧解,应尽量避免小题大做,否则将导致后面的解答题没有充裕的时间思考而后悔惋惜.
一、特例法
当填空题或选择题的结论唯一或题设条件中提供的信息暗示答案是一个定值或是范围可猜想时,可以把题中变化的不定量用特殊值代替,包括选取符合题意的特殊数值、特殊位置、特殊函数、特殊数列、特殊图形、特殊猜想等,代入或者比照选项来确定答案。
(一)取特殊值
【例1】等差数列的前项和为30,前项和为100,则它的前项和为
【难度】★★
【答案】210
【解析】取,依题意,,则,又是等差数列,从而,故
【例2】 .
【难度】★★
【答案】
【解析】令,则.
【例3】函数在区间内的图象是( )
【难度】★★
【答案】D
【解析】利用特殊值代入即可,答案选D
(二)特殊函数
【例4】如果,那么下面的不等式恒成立的是 ( )
、 、 、 、
【难度】★★
【答案】
【解析】构造函数,易证是上的奇函数且单调递增,由题中条件可得,即。
【例5】已知是定义在上的函数,且,对任意都有下列两式成立:(1);(2)若,则的值为___________
【难度】★★
【答案】1
【解析】令
【例6】如果函数对任意实数都有,那么的大小关系是 .
【难度】★★
【答案】
【解析】由于,故知的对称轴是.可取特殊函数,即可求得.∴.
(三)特殊数列
【例7】已知两个等差数列和的前项和分别为和,且,则使得为整数的正整数的个数有 个。
【难度】★★
【答案】5
【解析】因为等差数列的前项和为二次函数且没有常数项,不妨设,,代入求解可得,满足题意的正整数为1,2,3,5,11,共有5个。
【例8】在各项均为正数的等比数列中,若,则( )
A.12 B.10 C.8 D.
【难度】★★
【答案】B
【解析】因为答案唯一,故取一个满足条件的特殊数列即可,选B.
【例9】已知是公差不为零的等差数列,如果是的前项和,那么_________
【难度】★★
【答案】2
【解析】特别取,有,于是有,故应填2。
(四)特殊图形
【例10】已知在中,,,为的外心,则
【难度】★★
【答案】32
【解析】因为图形的不确定性,但能猜到题中的结果是定值,将变成即可。
【例11】在△ABC中,角A、B、C所对的边分别为、、.若、、成等差数列,则 .
【难度】★★
【答案】
【解析】特殊化:令,则△ABC为直角三角形,,从而所求值为.
【例12】已知是直线,是平面,给出下列命题:①若,则∥;②若,则∥;③若内不共线的三点到的距离都相等,则∥;④若,且∥,∥,则∥;⑤若为异面直线,,∥,,∥,则∥.
则其中正确的命题是 .(把你认为正确的命题序号都填上)
【难度】★★
【答案】②⑤
【解析】依题意可取特殊模型正方体AC1(如图),在正方体AC1中逐一判断各命题,易得正确的命题是②⑤.
(五)特殊猜想
【例13】线段的长度为2,点分别在非负半轴和非负半轴上滑动,以线段为一边,在第一象限内作矩形(顺时针排序),,设为坐标原点,则的取值范围是 .
【难度】★★★
【答案】
【解析】由于图形的对称性效果,我们不难猜测,在两点关于直线对称时取得最大值,在两点中有一点和原点重合时取得最小值。
【例14】给定两个长度为1的平面向量夹角为.如图所示,点C在以O为圆心的圆弧上变动.若,则的最大值是________.
【难度】★★
【答案】2
【解析】图形本身的特殊性。
【例15】已知椭圆C:的上、下焦点分别为、,过椭圆C上一点作倾斜角互补的两条直线PA、PB,分别交椭圆C于A、B两点,则直线AB的斜率为 .
【难度】★★
【答案】
【解析】易知直线的斜率只能由椭圆和的坐标确定,和圆的方式进行类比,先猜后求。
【巩固训练】
1.若对于任意的实数,有,则的值为
【难度】★★
【答案】6
【解析】对实数取4个具体的实数,代入已知等式中得到方程组,即可求出的值。
2.设函数是定义在上,则函数与函数的图像关于 ( )
直线对称 直线对称 直线对称 直线对称
【难度】★★
【答案】D
【解析】令,则,,显然两函数关于对称。
3.设函数是定义在上的奇函数,且当时,单调递减,若数列是等差数列,且,则的值( )
A.恒为正数 B.恒为负数 C.恒为0 D.可正可负
【难度】★★
【答案】A
【解析】令,即可。
4.已知一9行9列的矩阵中的元素是由互不相等的81个数组成,若每行9个数与每列的9个数按表中顺序分别构成等差数列,且正中间一个数,则矩阵中所有元素之和为__________.
【难度】★★
【答案】567
【解析】用正整数数列排布即可。
5.若数列为等差数列,分别为其前项和,且,则
【难度】★★
【答案】
【解析】取两组和观察即可得。
6.△ABC的外接圆的圆心为O,两条边上的高的交点为H,,则的取值是 .
【难度】★★
【答案】1
【解析】特殊化处理,不妨设△ABC为直角三角形,则圆心O在斜边中点处,此时有,.
7.已知SA,SB,SC两两所成角均为60°,则平面SAB与平面SAC所成的二面角为 .
【难度】★★
【答案】
【解析】取SA=SB=SC,则在正四面体S-ABC中,易得平面SAB与平面SAC所成的二面角为.
8.在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足=,则·的取值范围是________.
【难度】★★
【答案】
【解析】取端点计算,再进行检验和比较。
9.已知等差数列的首项为,公差为,前项和为,数列也为等差数列且公差与的公差相同,则
【难度】★★
【答案】
【解析】利用奇数数列去猜想类比即可。
二、排除法(代入检验法)
【例16】函数y=2x -的图像大致是( )
【难度】★★
【答案】A
【解析】因为当所以排除B,C;故排除D,选A
【例17】如图,单位圆中的长度为,表示
与弦AB所围成的弓形的面的2倍,则
函数的图象是( )
A. B. C. D.
【难度】★★
【答案】D
【解析】结合直觉法逐一验证。显然,面积不是弧长的一次函数,排除A;当从很小的值逐渐增大时,的增长不会太快,排除B;只要则必然有面积,排除C,选D。事实上,直觉好的学生完全可以直接选D.
【例18】给出下列三个命题:
①函数与是同一函数;高☆考♂资♀源*网②若函数与的图像关于直线对称,则函数与的图像也关于直线对称;③若奇函数对定义域内任意x都有,则为周期函数。其中真命题是( )
A. ①② B. ①③ C.②③ D. ②
【难度】★★
【答案】C
【解析】考查相同函数、函数对称性的判断、周期性知识。考虑定义域不同,①错误;排除A、B,验证③, ,又通过奇函数得,所以f(x)是周期为2的周期函数,选择C。
【例19】在题设条件中的△ABC的三边a、b、c满足等式acosA+bcosB=ccosC,则此三角形必是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形
C.等边三角形 D.其他三角形
【难度】★★
【答案】D
【解析】题设条件中的等式是关于、A与、B的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有,即,矛盾,从而C被淘汰,故选D.
【巩固训练】
1.将函数的图象按向量平移以后的图象如图所示,则
平移以后的图象所对应的函数解析式是( )
A. B.
C. D.
【难度】★
【答案】C
【解析】若选A或B,则周期为,与图象所示周期不符;若选D,则与 “按向量平移” 不符,选C.此题属于容易题.
2.某地一年内的气温Q(t)(℃)与时间t(月份)之间的关系如右图,已知
该年的平均气温为10℃。令C(t)表示时间段[0,t]的平均气温,C(t)与t之
间的函数关系如下图,则正确的应该是( )
A、 B、 C、 D、
【难度】★★
【答案】A
【解析】由图可以发现,t=6时,C(t)=0,排除C;t=12时,C(t)=10,排除D;t>6时的某一段气温超过10℃,排除B,选A.
3.对于抛物线上任意一点Q,点P(a,0)都满足,则的取值范围是( )
A. B. C. D.
【难度】★★
【答案】B
【解析】用逻辑排除法.画出草图,知a<0符合条件,则排除C、D;又取,则P是焦点,记点Q到准线的距离为d,则由抛物线定义知道,此时a<d<|PQ|,即表明符合条件,排除A,选B.
4.函数的一个单调增区间是( )
A. B. C. D.
【难度】★★
【答案】A
【解析】因为函数是连续的,选项里面的各个端点值其实是可以取到的,由,显然直接排除D,在A、B、C中只要计算两个即可,因为B中代入会出现,所以最好只算A、C、现在就验算A,有,符合,选A.
三、等价转化
【例20】如果不等式的解集为A,且,那么实数的取值范围是 。
【难度】★★
【答案】
【解析】根据不等式解集的几何意义,作函数和函数的图象,从图上得出实数的范围是。
【例21】已知函数是定义域为的偶函数. 当时, 若关于的方程有且只有7个不同实数根,则实数的取值范围是 .
【难度】★★★
【答案】
【解析】,则方程转化为,设为
两个根,由于方程有且只有7个不同实数根,则一共有7个不同的根,结合与的图像易知,由韦达定理知,故
【例22】抛物线的焦点为F,点为该抛物线上的动点,又点,则的最小值为 .
【难度】★★★
【答案】
【解析】如图所示,作与点,则有
使最小,即使最小,只需要最小即可,即只需要最小即可,
设,
当且仅当等号成立,最小为1,故最小为
故.
【例23】
【难度】★★
【答案】
【解析】
【巩固训练】
1.若关于x的方程=k(x-2)有两个不等实根,则k的取值范围是
【难度】★★
【答案】
【解析】令y1=,y2=k(x-2),由图14-3可知kAB
2.已知不等式的解集为,则 ,且的值为
【难度】★★★
【答案】
【解析】将不等式解集问题转化为方程根的问题,可看做夹在与部分的图像对应的的范围为,由图像易知:可解得
3.已知函数若对于正数(),直线与函数的图像恰有个不同交点,则______.
【难度】★★★
【答案】
【解析】结合图像知与第个半圆相切时直线与函数的图像恰有个不同交点,将问题可以转化为到的为1得,化简得,.
4.函数在区间上可找到个不同数,,……,,使得,则的最大值等于( )
8 9 10 11
【难度】★★★
【答案】
【解析】令,则可转化为的交点问题,如图所示:当时最多出现10个交点.
解答填空题时,由于不反映过程,只要求结果,故对正确性的要求比解答题更高、更严格,《考试说明》中对解答填空题提出的基本要求是“正确、合理、迅速”.为此在解填空题时要做到:快——运算要快,力戒小题大作;稳——变形要稳,不可操之过急;全——答案要全,力避残缺不齐;活——解题要活,不要生搬硬套;细——审题要细,不能粗心大意.
解选择题的基本思想是既要看到各类常规题的解题思想,但更应看到选择题的特殊性,数学选择题的四个选择中有且仅有一个是正确的,因而,在解答时应该突出一个“选”字,尽量减少书写解题过程,要充分利用题干和选择支两方面提供的信息,依据题目的具体特点,灵活、巧妙、快速地选择解法,以便快速智取,这是解选择题的基本策略.
1.已知,那么=_____.
【难度】★★
【答案】
2.三棱柱中,若、分别为、的中点,平面将三棱柱分成体积为和两部分(),那么 .
【难度】★★
【答案】
3.己知定义在上的奇函数满足,且在区间上是增函数,若方程在区间上有四个不同的根,,,,则 .
【难度】★★
【答案】-8
4.某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为,则该队员每次罚球的命中率为____________.
【难度】★★
【答案】
【解析】等价转化为求它的对立事件即可,由得
5.己知函数与互为反函数,又与的图像关于直线对称,若, .
【难度】★★
【答案】
6.直线与曲线()的公共点的个数是 .
【难度】★★
【答案】4
【解析】取,原方程变为,这是两个椭圆,与直线有4个公共点.
7.设,则下列不等式中,正确的是( )
A、
B、
C、
D、
【难度】★★
【答案】C
8.若,则( )
A.(,) B.(,0) C.(0,) D.(,)
【难度】★★
【答案:B】
9.若,P=,Q=,R=,则( )
A.RPQ B.PQ R C.QPR D.P RQ
【难度】★★
【答案】B
10.函数的定义域为,值域为,变动时,方程表示的图形可以是 ( )
A. B. C. D.
【难度】★★
【答案】B
【解析】取选项中的特殊点代入检验即可。
11.方程的解可视为函数的图像与函数的图像交点的横坐标。若方程的各个实根,,,所对应的点均在直线的同侧,则实数的取值范围是 .
【难度】★★★
【答案】或
【解析】将方程转化成函数的交点和单调性即可。
12.设函数的定义域为,若对于任意、,当时,恒有,则称点为函数图像的对称中心.研究函数的某一个对称中心,并利用对称中心的上述定义,可得到的值为……………………( )
A. B. C. D.
【难度】★★★
【答案】D
【解析】观察会考虑到该函数具对称中心
,即函数的对称中心为。
知识梳理
例题解析
C
B
x
O
y
A
D
B
O
A
C
2
2
2
2
2
2
2
2
反思总结
课后练习
a
b
O
-4
4
a
b
O
4
-4
a
b
O
4
-4
a
b
O
-4
4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
