苏科版数学七下第九章整式的乘法与因式分解章末复习学案(习题无答案)
文档属性
| 名称 | 苏科版数学七下第九章整式的乘法与因式分解章末复习学案(习题无答案) | 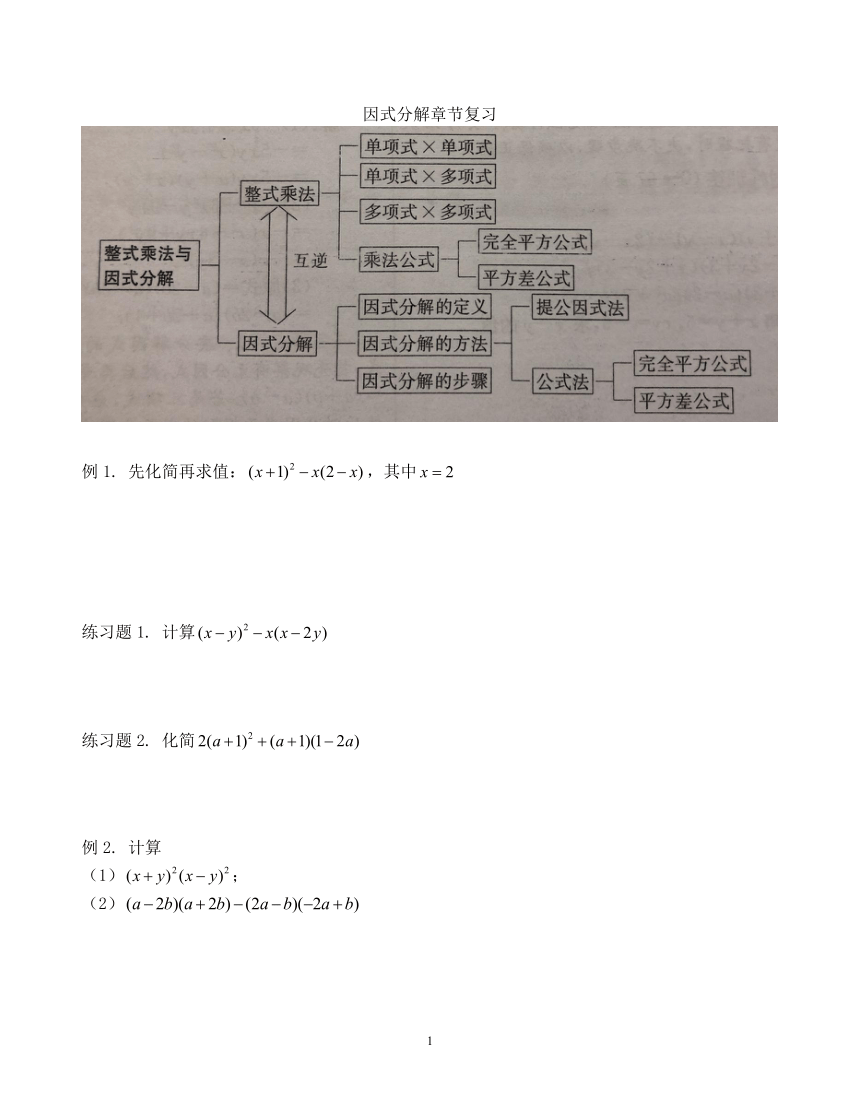 | |
| 格式 | zip | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 12:22:03 | ||
图片预览




文档简介
因式分解章节复习
例1. 先化简再求值:,其中 练习题1. 计算 练习题2. 化简 例2. 计算 (1); (2) 练习题3. 计算 (1); (2); (3); (4)已知,求的值. 例3. 分解因式. (1); (2); (3). 练习题4. 把下列各式分解因式 (1); (2). 真题剖析 例1. 因式分解________________________. 例2. 先化简,再求值:,其中. 练习题1. 分解因式_______________________. 练习题2. 化简_______________________. 练习题3. 化简. 专题突破 例1. 已知,求代数式的值. 例2. 计算. 例3. 如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化. (1)求出绿地的面积;(用含a、b的代数式表示) (2)若a=2b,且道路的面积为224平分米,求原长方形空地的宽. 例4. 观察下列等式: 第一行 第二行 第三行 第四行 …… (1)请你写出第五行的等式为_____________________; (2)按照上述规律,第n行的等式为_____________________; (3)请你利用已学过的知识对你得到的等式进行说明. 例5. 已知,求的值. 一、选择题 1.若( ) A.1 B.-2 C.-1 D.2 2.多项式,,,,,,中,能在有理数范围内用平方差公式分解的有( ) A.2个 B.3个 C.4个 D.5个 3.下列运算正确的是( ) A. B. C. D. 4.运用乘法公式计算正确的是( ) A. B. C. D. 5.下列因式分解正确的是( ) A. B. C. D. 6.多项式各项的公因式为( ) A. B. C. D. 7.如果多项式能分解为一个二项式的平方的形式,那么m的值为( ) A.12 B.2 C.-24 D. 8.利用图形中面积的等量关系可以得到某些数学公式。例如,根据图甲,我们可以得到两数和的平方公式:。你根据图乙能得到的数学公式是( ) A. B. C. D. 二、填空题 9.图中的四边形均为长方形,根据图形,写出一个正确的等式:___________________. 10. 如果,,那么代数式的值是___________________. 11.已知,则代数式的值是___________________. 12. 计算的结果是___________________. 13. 当时,_________________. 14. (____________). 15. 如果是完全平方式,那么a的值是_________________. 16.当x=________时,多项式取得最小值. 17.已知,则_________________. 18.若,则的值为________________. 三、解答题 19. 用简便方法计算. (1); (2); (3). 20.计算 (1); (2); (3). 21.因式分解 22.解方程 23.将一条长40cm的金色彩带剪成两段,恰好可用来镶嵌两张大小不同的正方形壁画的边(不计接头处),已知两张壁画的面积相差40,问这条金色彩带应剪成多长的两段? 24.先化简,再求值:,其中. 25.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为"神秘数".如:,,,因此4,6,12都是"神秘数". (1)28和2012这两个数是"神秘数"吗?为什么? (2)设两个连续偶数为和(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么? (3)两个连续奇数的平方数(取正数)是神秘数吗?为什么? 26.乘法公式的探究及应用. (1)如图1,可以求出阴影部分的面积是______________ (写成两数平方差的形式); (2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______ ,长是______ ,面积是______________ (写成多项式乘法的形式); (3)比较左、右两图的阴影部分面积,可以得到乘法公式_____________ (用式子表达). 27.下面是某同学对多项式进行因式分解的过程. 解:设, 则原式 =(第一步) =(第二步) =(第三步) =(第四步) (1)该同学第二步到第三步运用了因式分解的 ( ) A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式 (2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果 . (3)请你模仿以上方法尝试对多项式进行因式分解.
8
例1. 先化简再求值:,其中 练习题1. 计算 练习题2. 化简 例2. 计算 (1); (2) 练习题3. 计算 (1); (2); (3); (4)已知,求的值. 例3. 分解因式. (1); (2); (3). 练习题4. 把下列各式分解因式 (1); (2). 真题剖析 例1. 因式分解________________________. 例2. 先化简,再求值:,其中. 练习题1. 分解因式_______________________. 练习题2. 化简_______________________. 练习题3. 化简. 专题突破 例1. 已知,求代数式的值. 例2. 计算. 例3. 如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化. (1)求出绿地的面积;(用含a、b的代数式表示) (2)若a=2b,且道路的面积为224平分米,求原长方形空地的宽. 例4. 观察下列等式: 第一行 第二行 第三行 第四行 …… (1)请你写出第五行的等式为_____________________; (2)按照上述规律,第n行的等式为_____________________; (3)请你利用已学过的知识对你得到的等式进行说明. 例5. 已知,求的值. 一、选择题 1.若( ) A.1 B.-2 C.-1 D.2 2.多项式,,,,,,中,能在有理数范围内用平方差公式分解的有( ) A.2个 B.3个 C.4个 D.5个 3.下列运算正确的是( ) A. B. C. D. 4.运用乘法公式计算正确的是( ) A. B. C. D. 5.下列因式分解正确的是( ) A. B. C. D. 6.多项式各项的公因式为( ) A. B. C. D. 7.如果多项式能分解为一个二项式的平方的形式,那么m的值为( ) A.12 B.2 C.-24 D. 8.利用图形中面积的等量关系可以得到某些数学公式。例如,根据图甲,我们可以得到两数和的平方公式:。你根据图乙能得到的数学公式是( ) A. B. C. D. 二、填空题 9.图中的四边形均为长方形,根据图形,写出一个正确的等式:___________________. 10. 如果,,那么代数式的值是___________________. 11.已知,则代数式的值是___________________. 12. 计算的结果是___________________. 13. 当时,_________________. 14. (____________). 15. 如果是完全平方式,那么a的值是_________________. 16.当x=________时,多项式取得最小值. 17.已知,则_________________. 18.若,则的值为________________. 三、解答题 19. 用简便方法计算. (1); (2); (3). 20.计算 (1); (2); (3). 21.因式分解 22.解方程 23.将一条长40cm的金色彩带剪成两段,恰好可用来镶嵌两张大小不同的正方形壁画的边(不计接头处),已知两张壁画的面积相差40,问这条金色彩带应剪成多长的两段? 24.先化简,再求值:,其中. 25.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为"神秘数".如:,,,因此4,6,12都是"神秘数". (1)28和2012这两个数是"神秘数"吗?为什么? (2)设两个连续偶数为和(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么? (3)两个连续奇数的平方数(取正数)是神秘数吗?为什么? 26.乘法公式的探究及应用. (1)如图1,可以求出阴影部分的面积是______________ (写成两数平方差的形式); (2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______ ,长是______ ,面积是______________ (写成多项式乘法的形式); (3)比较左、右两图的阴影部分面积,可以得到乘法公式_____________ (用式子表达). 27.下面是某同学对多项式进行因式分解的过程. 解:设, 则原式 =(第一步) =(第二步) =(第三步) =(第四步) (1)该同学第二步到第三步运用了因式分解的 ( ) A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式 (2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果 . (3)请你模仿以上方法尝试对多项式进行因式分解.
8
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
