沪教版六年级下册数学:5.8 有理数的乘方课件(共16张PPT)
文档属性
| 名称 | 沪教版六年级下册数学:5.8 有理数的乘方课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
有理数的乘方
有理数
第1课时 有理数的乘方
1.理解并掌握有理数的乘方、幂、底数、指 数的概念及意义;(难点)
2.能够正确进行有理数的乘方运算.(重点)
导入新课
复习引入
多个因数的乘法的法则:
几个不为零的数相乘,积的符号由_____________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
几个数相乘,有一个因数为0,_________
负因数的个数
奇数
偶数
积为0
请同学们看看下面的乘法算式,你发现了什么?
这就是我们这节课所要探讨的内容——有理数的乘方
相同因数的乘法
讲授新课
如图,一正方形的边长为5cm,则它的面积
为________平方厘米;
一正方体的棱长为5cm, 则它的体积为___________立方厘米.
5
5
探究新知
5×5×5
5×5
5×5×5 记作:
5×5×5×5×5×5记作:
如果是任意多个相同的有理数相乘,我们如何去简化表示呢?
53
56
相同因数的乘法如何简化?
5×5记作:
52
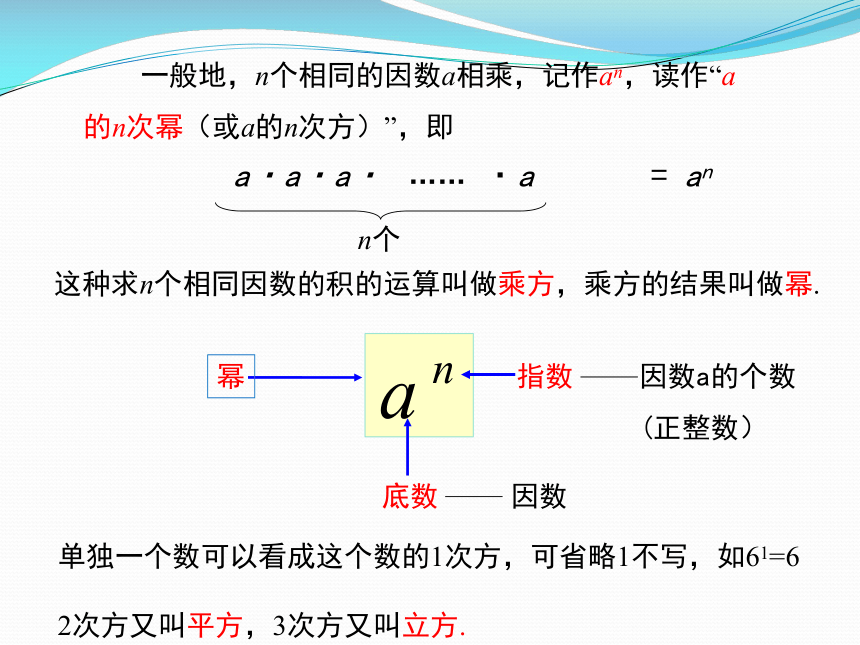
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
单独一个数可以看成这个数的1次方,可省略1不写,如61=6
2次方又叫平方,3次方又叫立方.
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示_____个 相乘,读作 的____次方,也读作 的 次幂,其中 叫做 ,6叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
填一填
-5
2
-5
-5
平方
6
6
6
底数
指数
例1 计算:
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
思考:1.你发现底数为负数的幂的正负有什么规律?
负数的奇次方取负号,负数的偶次方取 正号
例2 计算:
(1) 43; (2) 24; (3)
解:(1) 43=4×4×4=64;
(2) 24=2×2×2×2=16;
思考:2.你发现底数为正数的幂的正负 有什么规律?
正数的任何次方都取正号
归纳总结
正数的任何次方都取正号;
负数的奇次方取负号,负数的偶次方取 正号;
0的任何正整数次方都是0.
根据有理数的乘法法则,可得乘方运算法则:
非0有理数的乘方,将其绝对值乘方,而结果的符号是:
3.我们知道不管多少个0相乘,仍得0
0的任何正整数次方都是0
课后练习抢答
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方,(-4)2=(-4)×(-4)=16
-42表示4的平方的相反数, -42= -4×4= -16
当底数是负数或分数时,底数一定要加上括号.
议一议
当堂练习
1.填空:(其中n为正整数)
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; (4)0.13= ;
(5)(-1)9= ; (6)(-1)12= ;
(7)(-1)2n= ; (8)(-1)2n+1= ;
(9)(-1)n=
____________________.
-9
-9
-125
0.001
-1
1
1
-1
(当n为奇数时)
(当n为偶数时)
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次方都是正数
(2)负数的奇次方是负数,负数的偶次方是正数
(3)零的正整数次幂都是零
3.注意:
二者的区别及相互关系;
的区别.
课堂小结
1.《导学测试》本课时练习
2.预习下一节内容:加减乘除乘方混合运算
课后作业
有理数的乘方
有理数
第1课时 有理数的乘方
1.理解并掌握有理数的乘方、幂、底数、指 数的概念及意义;(难点)
2.能够正确进行有理数的乘方运算.(重点)
导入新课
复习引入
多个因数的乘法的法则:
几个不为零的数相乘,积的符号由_____________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
几个数相乘,有一个因数为0,_________
负因数的个数
奇数
偶数
积为0
请同学们看看下面的乘法算式,你发现了什么?
这就是我们这节课所要探讨的内容——有理数的乘方
相同因数的乘法
讲授新课
如图,一正方形的边长为5cm,则它的面积
为________平方厘米;
一正方体的棱长为5cm, 则它的体积为___________立方厘米.
5
5
探究新知
5×5×5
5×5
5×5×5 记作:
5×5×5×5×5×5记作:
如果是任意多个相同的有理数相乘,我们如何去简化表示呢?
53
56
相同因数的乘法如何简化?
5×5记作:
52
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
单独一个数可以看成这个数的1次方,可省略1不写,如61=6
2次方又叫平方,3次方又叫立方.
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示_____个 相乘,读作 的____次方,也读作 的 次幂,其中 叫做 ,6叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
填一填
-5
2
-5
-5
平方
6
6
6
底数
指数
例1 计算:
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
思考:1.你发现底数为负数的幂的正负有什么规律?
负数的奇次方取负号,负数的偶次方取 正号
例2 计算:
(1) 43; (2) 24; (3)
解:(1) 43=4×4×4=64;
(2) 24=2×2×2×2=16;
思考:2.你发现底数为正数的幂的正负 有什么规律?
正数的任何次方都取正号
归纳总结
正数的任何次方都取正号;
负数的奇次方取负号,负数的偶次方取 正号;
0的任何正整数次方都是0.
根据有理数的乘法法则,可得乘方运算法则:
非0有理数的乘方,将其绝对值乘方,而结果的符号是:
3.我们知道不管多少个0相乘,仍得0
0的任何正整数次方都是0
课后练习抢答
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方,(-4)2=(-4)×(-4)=16
-42表示4的平方的相反数, -42= -4×4= -16
当底数是负数或分数时,底数一定要加上括号.
议一议
当堂练习
1.填空:(其中n为正整数)
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; (4)0.13= ;
(5)(-1)9= ; (6)(-1)12= ;
(7)(-1)2n= ; (8)(-1)2n+1= ;
(9)(-1)n=
____________________.
-9
-9
-125
0.001
-1
1
1
-1
(当n为奇数时)
(当n为偶数时)
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次方都是正数
(2)负数的奇次方是负数,负数的偶次方是正数
(3)零的正整数次幂都是零
3.注意:
二者的区别及相互关系;
的区别.
课堂小结
1.《导学测试》本课时练习
2.预习下一节内容:加减乘除乘方混合运算
课后作业
