18.2.1 矩形导学案(共2课时、无答案)
文档属性
| 名称 | 18.2.1 矩形导学案(共2课时、无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 21.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 12:40:58 | ||
图片预览

文档简介
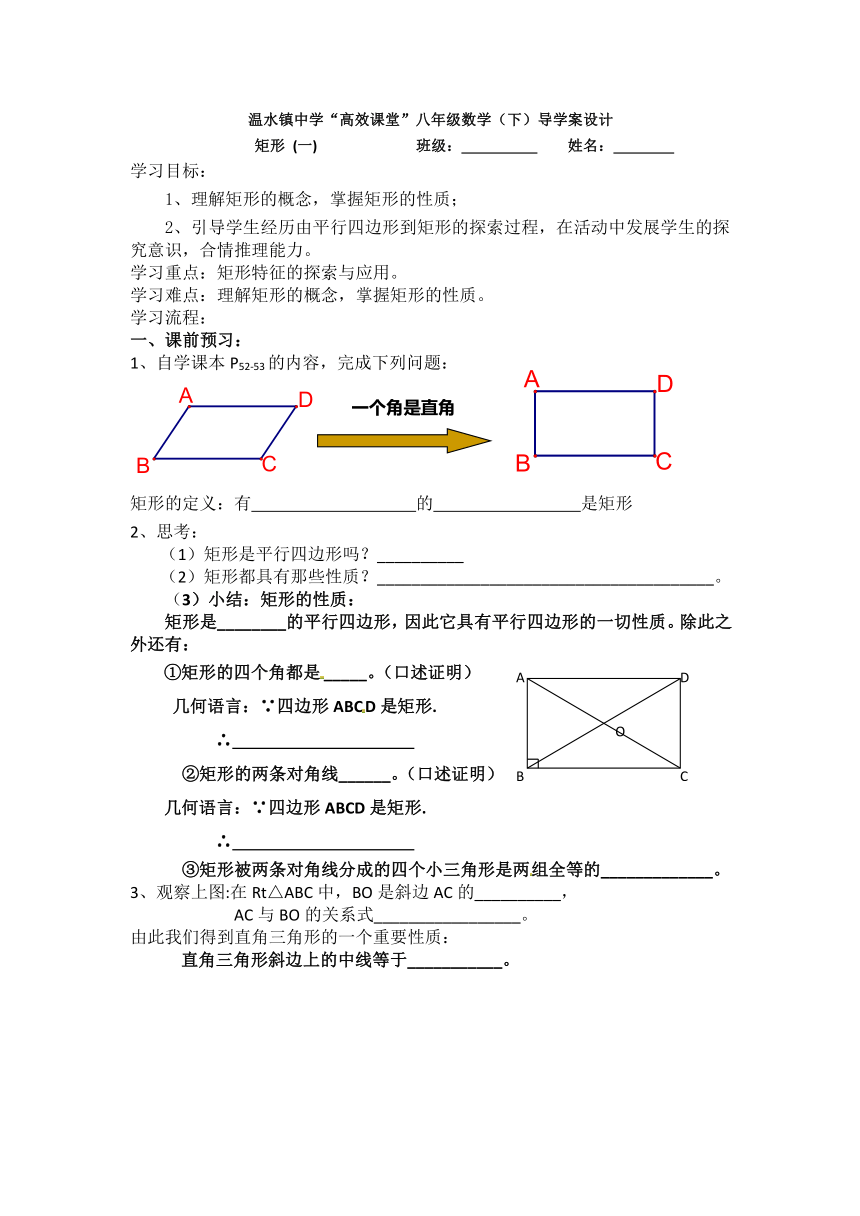
温水镇中学“高效课堂”八年级数学(下)导学案设计
矩形 (一) 班级: 姓名:
学习目标:
1、理解矩形的概念,掌握矩形的性质;
2、引导学生经历由平行四边形到矩形的探索过程,在活动中发展学生的探究意识,合情推理能力。
学习重点:矩形特征的探索与应用。
学习难点:理解矩形的概念,掌握矩形的性质。
学习流程:
一、课前预习:
1、自学课本P52-53的内容,完成下列问题:
矩形的定义:有 的 是矩形
2、思考:
(1)矩形是平行四边形吗?__________
(2)矩形都具有那些性质?_______________________________________。
(3)小结:矩形的性质:
矩形是________的平行四边形,因此它具有平行四边形的一切性质。除此之外还有:
①矩形的四个角都是_____。(口述证明)
几何语言:∵四边形ABCD是矩形.
∴
②矩形的两条对角线______。(口述证明)
几何语言:∵四边形ABCD是矩形.
∴
③矩形被两条对角线分成的四个小三角形是两组全等的_____________。
3、观察上图:在Rt△ABC中,BO是斜边AC的__________,
AC与BO的关系式_________________。
由此我们得到直角三角形的一个重要性质:
直角三角形斜边上的中线等于___________。
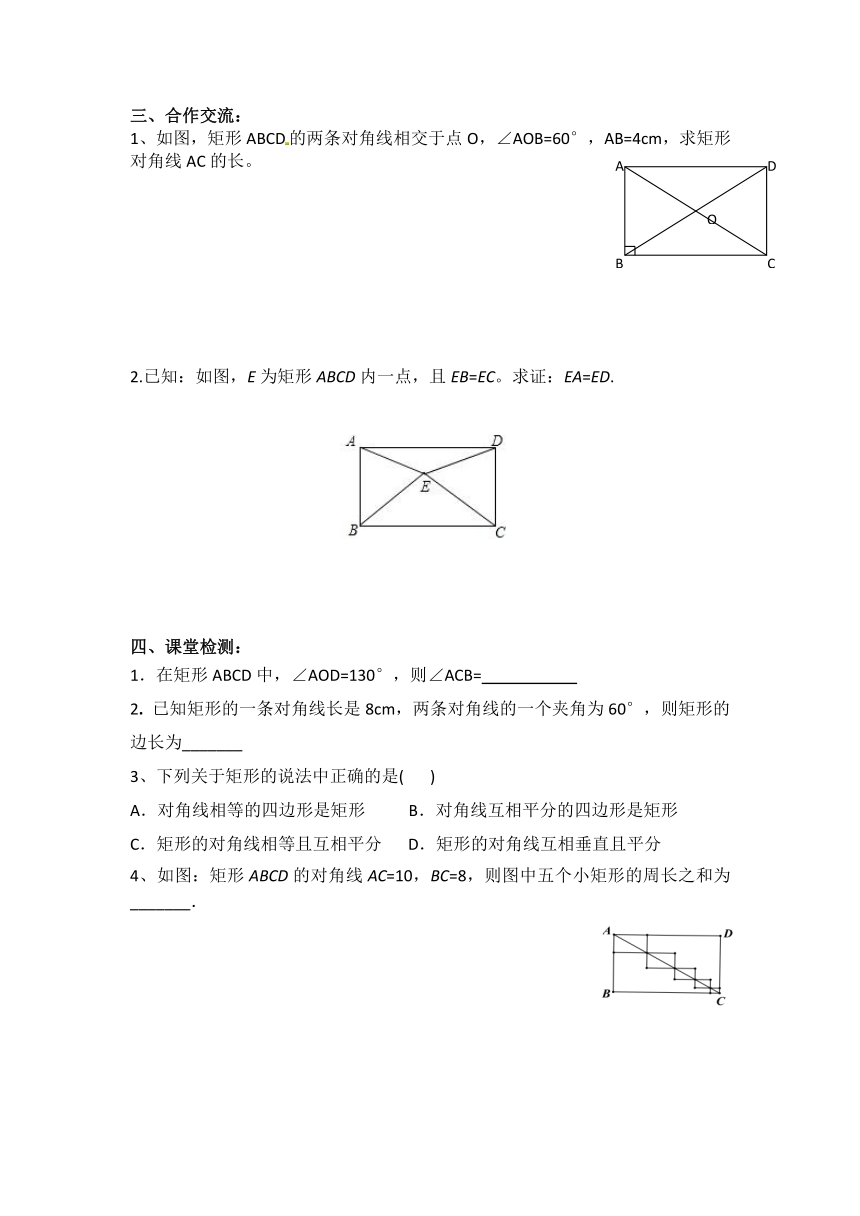
三、合作交流:
1、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线AC的长。
2.已知:如图,E为矩形ABCD内一点,且EB=EC。求证:EA=ED.
四、课堂检测:
1.在矩形ABCD中,∠AOD=130°,则∠ACB=
2. 已知矩形的一条对角线长是8cm,两条对角线的一个夹角为60°,则矩形的边长为_______
3、下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线相等且互相平分 D.矩形的对角线互相垂直且平分
4、如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为_______.
温水镇中学“高效课堂”八年级数学(下)导学案设计
矩形 (二) 班级: 姓名:
学习目标:
理解并掌握矩形的判定方法.
使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
重点、难点
重点:矩形的判定.
难点:矩形的判定及性质的综合应用.
学习流程:
一、课前预习:
1.矩形是轴对称图形,它有______条对称轴.
2.想一想:矩形有哪些性质?在这些性质中那些是平行四边形所没有的?列表进行比较.
平行四边形 矩形
边
角
对角线
3、怎样判定一个平行四边形是矩形呢?
二、互动探究:
1、讨论:由矩形的定义可知:有_________________的平行四边形是矩形。
2、思考:由矩形的性质:①矩形对角线相等;②矩形四个角是直角。可得:
(1)对角线相等的平行四边形是矩形吗?
尝试证明:如图,□ABCD的对角线AC、BD相交于点O,AC=BD,
求证:□ABCD是矩形
(2)有三个角是直角的四边形是矩形吗?
尝试证明:如图,四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形
3、小结:矩形的判定方法:
(1)有一个角________的___________是矩形。
(2)对角线__________的___________是矩形。
(3)有三个角________的___________是矩形。
三、合作交流:
已知□ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
四、课堂检测:
1、下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
2.满足下列条件( )的四边形是矩形。
A.有三个角相等
B.有一个角是直角
C.对角线相等且互相垂直
D.对角线相等且互相平分
一个角是直角
A
B
C
D
O
A
B
C
D
O
矩形 (一) 班级: 姓名:
学习目标:
1、理解矩形的概念,掌握矩形的性质;
2、引导学生经历由平行四边形到矩形的探索过程,在活动中发展学生的探究意识,合情推理能力。
学习重点:矩形特征的探索与应用。
学习难点:理解矩形的概念,掌握矩形的性质。
学习流程:
一、课前预习:
1、自学课本P52-53的内容,完成下列问题:
矩形的定义:有 的 是矩形
2、思考:
(1)矩形是平行四边形吗?__________
(2)矩形都具有那些性质?_______________________________________。
(3)小结:矩形的性质:
矩形是________的平行四边形,因此它具有平行四边形的一切性质。除此之外还有:
①矩形的四个角都是_____。(口述证明)
几何语言:∵四边形ABCD是矩形.
∴
②矩形的两条对角线______。(口述证明)
几何语言:∵四边形ABCD是矩形.
∴
③矩形被两条对角线分成的四个小三角形是两组全等的_____________。
3、观察上图:在Rt△ABC中,BO是斜边AC的__________,
AC与BO的关系式_________________。
由此我们得到直角三角形的一个重要性质:
直角三角形斜边上的中线等于___________。
三、合作交流:
1、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线AC的长。
2.已知:如图,E为矩形ABCD内一点,且EB=EC。求证:EA=ED.
四、课堂检测:
1.在矩形ABCD中,∠AOD=130°,则∠ACB=
2. 已知矩形的一条对角线长是8cm,两条对角线的一个夹角为60°,则矩形的边长为_______
3、下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线相等且互相平分 D.矩形的对角线互相垂直且平分
4、如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为_______.
温水镇中学“高效课堂”八年级数学(下)导学案设计
矩形 (二) 班级: 姓名:
学习目标:
理解并掌握矩形的判定方法.
使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
重点、难点
重点:矩形的判定.
难点:矩形的判定及性质的综合应用.
学习流程:
一、课前预习:
1.矩形是轴对称图形,它有______条对称轴.
2.想一想:矩形有哪些性质?在这些性质中那些是平行四边形所没有的?列表进行比较.
平行四边形 矩形
边
角
对角线
3、怎样判定一个平行四边形是矩形呢?
二、互动探究:
1、讨论:由矩形的定义可知:有_________________的平行四边形是矩形。
2、思考:由矩形的性质:①矩形对角线相等;②矩形四个角是直角。可得:
(1)对角线相等的平行四边形是矩形吗?
尝试证明:如图,□ABCD的对角线AC、BD相交于点O,AC=BD,
求证:□ABCD是矩形
(2)有三个角是直角的四边形是矩形吗?
尝试证明:如图,四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形
3、小结:矩形的判定方法:
(1)有一个角________的___________是矩形。
(2)对角线__________的___________是矩形。
(3)有三个角________的___________是矩形。
三、合作交流:
已知□ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
四、课堂检测:
1、下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
2.满足下列条件( )的四边形是矩形。
A.有三个角相等
B.有一个角是直角
C.对角线相等且互相垂直
D.对角线相等且互相平分
一个角是直角
A
B
C
D
O
A
B
C
D
O
