2020年中考专题复习:动态问题(无答案)
文档属性
| 名称 | 2020年中考专题复习:动态问题(无答案) | 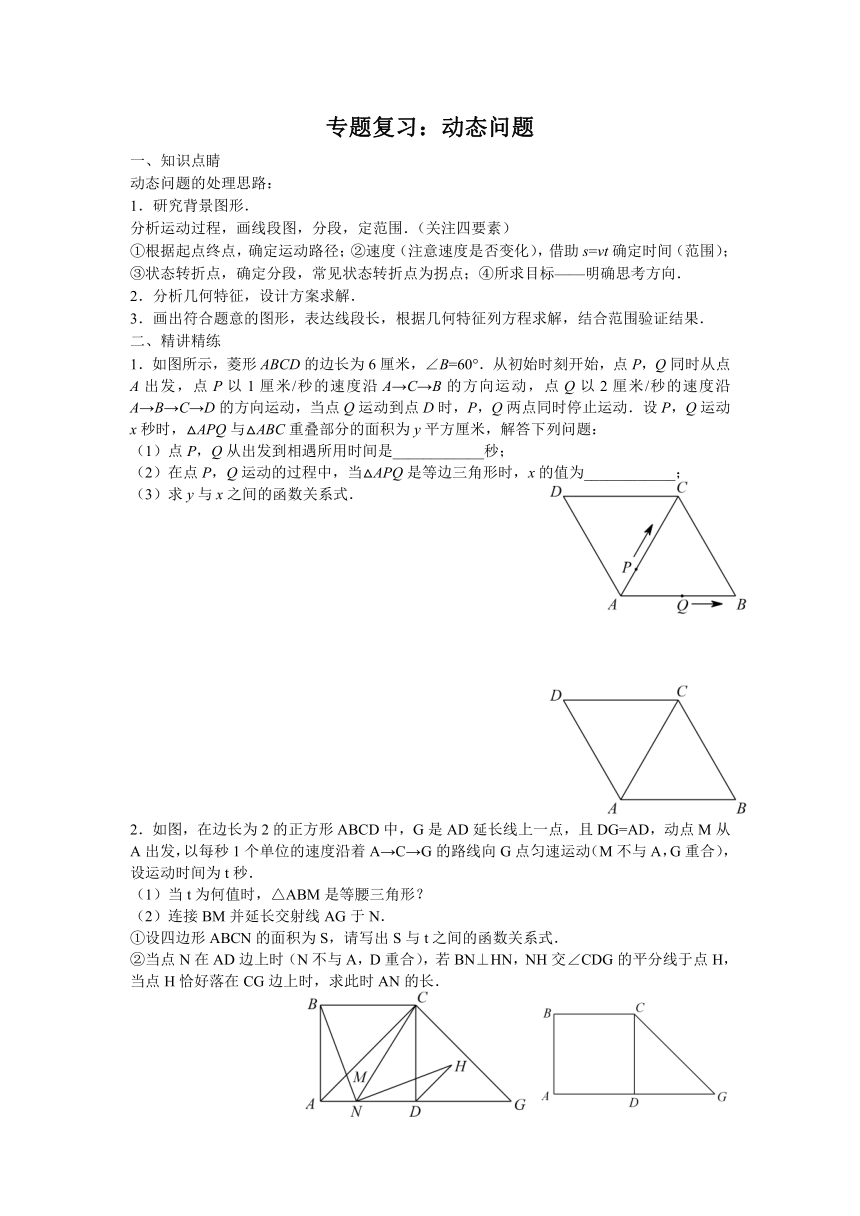 | |
| 格式 | zip | ||
| 文件大小 | 164.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 09:27:55 | ||
图片预览

文档简介
专题复习:动态问题
一、知识点睛
动态问题的处理思路:
1.研究背景图形.
分析运动过程,画线段图,分段,定范围.(关注四要素)
①根据起点终点,确定运动路径;②速度(注意速度是否变化),借助s=vt确定时间(范围);
③状态转折点,确定分段,常见状态转折点为拐点;④所求目标——明确思考方向.
2.分析几何特征,设计方案求解.
3.画出符合题意的图形,表达线段长,根据几何特征列方程求解,结合范围验证结果.
二、精讲精练
1.如图所示,菱形ABCD的边长为6厘米,∠B=60°.从初始时刻开始,点P,Q同时从点A出发,点P以1厘米/秒的速度沿A→C→B的方向运动,点Q以2厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到点D时,P,Q两点同时停止运动.设P,Q运动x秒时,△APQ与△ABC重叠部分的面积为y平方厘米,解答下列问题:
(1)点P,Q从出发到相遇所用时间是____________秒;
(2)在点P,Q运动的过程中,当△APQ是等边三角形时,x的值为____________;
(3)求y与x之间的函数关系式.
2.如图,在边长为2的正方形ABCD中,G是AD延长线上一点,且DG=AD,动点M从A出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒.
(1)当t为何值时,△ABM是等腰三角形?
(2)连接BM并延长交射线AG于N.
①设四边形ABCN的面积为S,请写出S与t之间的函数关系式.
②当点N在AD边上时(N不与A,D重合),若BN⊥HN,NH交∠CDG的平分线于点H,当点H恰好落在CG边上时,求此时AN的长.
一、知识点睛
动态问题的处理思路:
1.研究背景图形.
分析运动过程,画线段图,分段,定范围.(关注四要素)
①根据起点终点,确定运动路径;②速度(注意速度是否变化),借助s=vt确定时间(范围);
③状态转折点,确定分段,常见状态转折点为拐点;④所求目标——明确思考方向.
2.分析几何特征,设计方案求解.
3.画出符合题意的图形,表达线段长,根据几何特征列方程求解,结合范围验证结果.
二、精讲精练
1.如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数(k>0)的图象与直线AB相交于C、D两点,若S△OCA = S△OCD,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).
2.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,BC=6 cm,D是BC边上一点,且CD=1 cm.P,Q是直线BC上的两个动点,点P从点C出发,以1 cm/s的速度沿直线BC向右运动,同时,点Q从点D出发,以2 cm/s的速度也沿直线BC向右运动.以PQ为一边在BC上方作等边三角形PQR,下图是其运动过程中的某一位置,设运动的时间为t(s).
(1)△PQR的边长是______________cm;(用含t的代数式表示)
(2)设等边三角形PQR与△ABC重叠部分的面积为S(cm2),当时,求S与t之间的函数关系式.
一、知识点睛
动态问题的处理思路:
1.研究背景图形.
分析运动过程,画线段图,分段,定范围.(关注四要素)
①根据起点终点,确定运动路径;②速度(注意速度是否变化),借助s=vt确定时间(范围);
③状态转折点,确定分段,常见状态转折点为拐点;④所求目标——明确思考方向.
2.分析几何特征,设计方案求解.
3.画出符合题意的图形,表达线段长,根据几何特征列方程求解,结合范围验证结果.
二、精讲精练
1如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,且OA=OB=4.M是线段AB上一动点(不与点A,B重合),过点M作MC⊥OA于点C,MD⊥OB于点D.
(1)求直线AB的函数解析式.
(2)设点M的横坐标为x,四边形OCMD的面积为S1,求S1与x之间的函数关系式.当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)探究:当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向平行移动,设平移的距离为(),正方形OCMD与△AOB重叠部分的面积为S2,求S2与a之间的函数关系式.
2.如图1,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化.
(1)已知⊙M的圆心坐标为(4,2),半径为2.
当b=____________时,直线l:y=-2x+b(b≥0)经过圆心M;
当b=____________时,直线l:y=-2x+b(b≥0)与⊙M相切;
(2)若把⊙M换成矩形ABCD,如图2,其三个顶点的坐标分别为:A(2,0)、B(6,0)、
C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
一、知识点睛
动态问题的处理思路:
1.研究背景图形.
分析运动过程,画线段图,分段,定范围.(关注四要素)
①根据起点终点,确定运动路径;②速度(注意速度是否变化),借助s=vt确定时间(范围);
③状态转折点,确定分段,常见状态转折点为拐点;④所求目标——明确思考方向.
2.分析几何特征,设计方案求解.
3.画出符合题意的图形,表达线段长,根据几何特征列方程求解,结合范围验证结果.
二、精讲精练
1.如图所示,菱形ABCD的边长为6厘米,∠B=60°.从初始时刻开始,点P,Q同时从点A出发,点P以1厘米/秒的速度沿A→C→B的方向运动,点Q以2厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到点D时,P,Q两点同时停止运动.设P,Q运动x秒时,△APQ与△ABC重叠部分的面积为y平方厘米,解答下列问题:
(1)点P,Q从出发到相遇所用时间是____________秒;
(2)在点P,Q运动的过程中,当△APQ是等边三角形时,x的值为____________;
(3)求y与x之间的函数关系式.
2.如图,在边长为2的正方形ABCD中,G是AD延长线上一点,且DG=AD,动点M从A出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒.
(1)当t为何值时,△ABM是等腰三角形?
(2)连接BM并延长交射线AG于N.
①设四边形ABCN的面积为S,请写出S与t之间的函数关系式.
②当点N在AD边上时(N不与A,D重合),若BN⊥HN,NH交∠CDG的平分线于点H,当点H恰好落在CG边上时,求此时AN的长.
一、知识点睛
动态问题的处理思路:
1.研究背景图形.
分析运动过程,画线段图,分段,定范围.(关注四要素)
①根据起点终点,确定运动路径;②速度(注意速度是否变化),借助s=vt确定时间(范围);
③状态转折点,确定分段,常见状态转折点为拐点;④所求目标——明确思考方向.
2.分析几何特征,设计方案求解.
3.画出符合题意的图形,表达线段长,根据几何特征列方程求解,结合范围验证结果.
二、精讲精练
1.如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数(k>0)的图象与直线AB相交于C、D两点,若S△OCA = S△OCD,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).
2.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,BC=6 cm,D是BC边上一点,且CD=1 cm.P,Q是直线BC上的两个动点,点P从点C出发,以1 cm/s的速度沿直线BC向右运动,同时,点Q从点D出发,以2 cm/s的速度也沿直线BC向右运动.以PQ为一边在BC上方作等边三角形PQR,下图是其运动过程中的某一位置,设运动的时间为t(s).
(1)△PQR的边长是______________cm;(用含t的代数式表示)
(2)设等边三角形PQR与△ABC重叠部分的面积为S(cm2),当时,求S与t之间的函数关系式.
一、知识点睛
动态问题的处理思路:
1.研究背景图形.
分析运动过程,画线段图,分段,定范围.(关注四要素)
①根据起点终点,确定运动路径;②速度(注意速度是否变化),借助s=vt确定时间(范围);
③状态转折点,确定分段,常见状态转折点为拐点;④所求目标——明确思考方向.
2.分析几何特征,设计方案求解.
3.画出符合题意的图形,表达线段长,根据几何特征列方程求解,结合范围验证结果.
二、精讲精练
1如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,且OA=OB=4.M是线段AB上一动点(不与点A,B重合),过点M作MC⊥OA于点C,MD⊥OB于点D.
(1)求直线AB的函数解析式.
(2)设点M的横坐标为x,四边形OCMD的面积为S1,求S1与x之间的函数关系式.当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)探究:当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向平行移动,设平移的距离为(),正方形OCMD与△AOB重叠部分的面积为S2,求S2与a之间的函数关系式.
2.如图1,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化.
(1)已知⊙M的圆心坐标为(4,2),半径为2.
当b=____________时,直线l:y=-2x+b(b≥0)经过圆心M;
当b=____________时,直线l:y=-2x+b(b≥0)与⊙M相切;
(2)若把⊙M换成矩形ABCD,如图2,其三个顶点的坐标分别为:A(2,0)、B(6,0)、
C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
同课章节目录
