2.5.1 直线与圆的位置关系课件(共21张PPT)
文档属性
| 名称 | 2.5.1 直线与圆的位置关系课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 449.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 13:03:39 | ||
图片预览





文档简介
(共21张PPT)
直线与圆的位置关系
1.理解直线与圆相交、相切、相离的概念.
学习目标
2.会根据圆心到直线的距离与半径的大小关系,判断直线与圆的位置关系.
大家看日出时,在太阳升起过程中,太阳与地平线有什么关系?
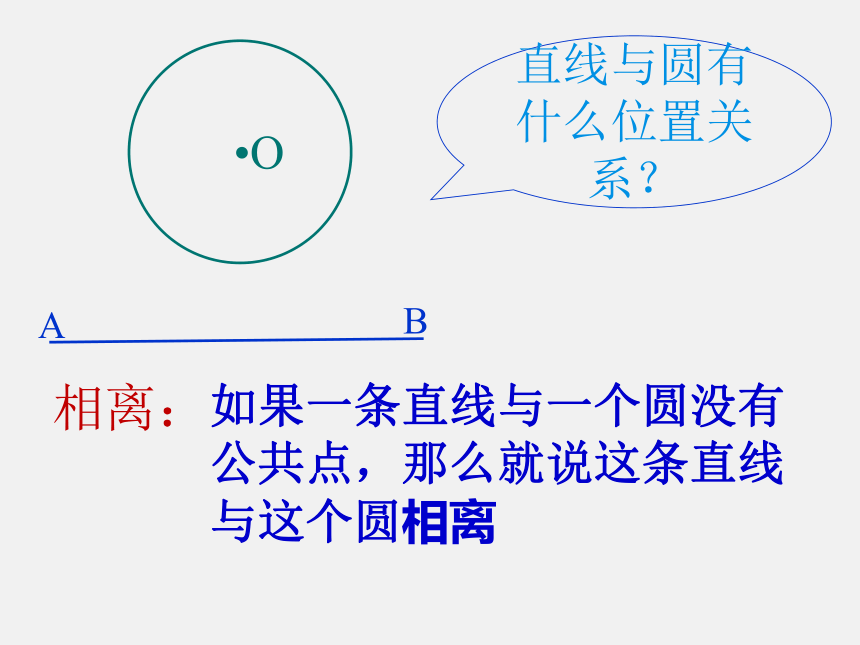
直线与圆有什么位置关系?
相离:
如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离
直线与圆有什么位置关系?
相离:
如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离
这时直线
与圆有什么关系?
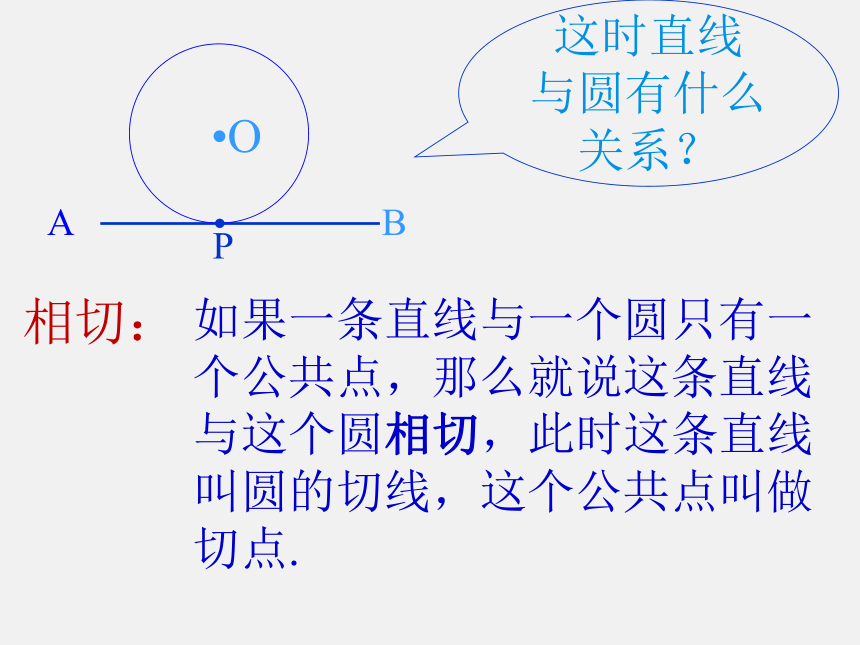
相切:
如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相切,此时这条直线 叫圆的切线,这个公共点叫做切点.
?
P
A
B
这时直线
与圆有什么关系?
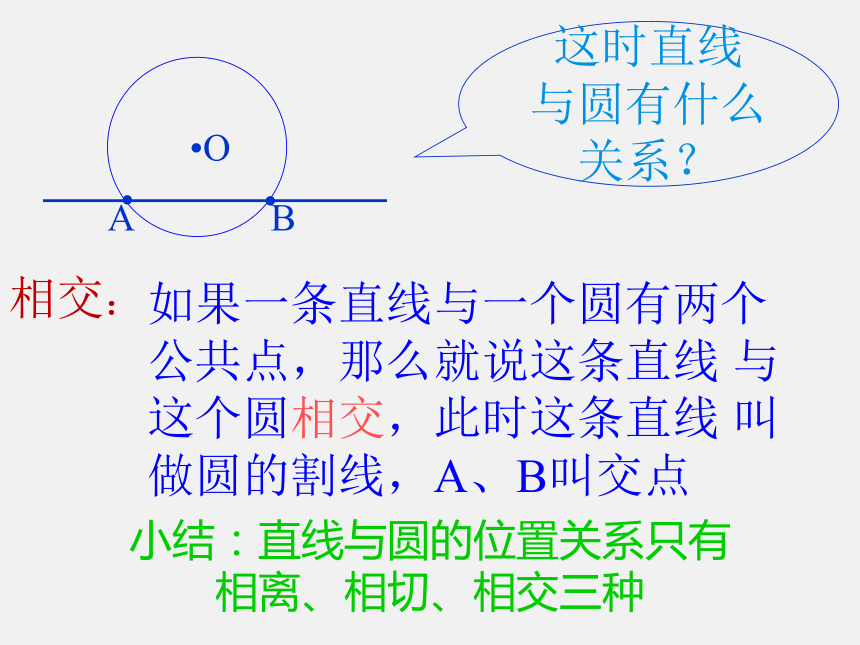
相交:
如果一条直线与一个圆有两个公共点,那么就说这条直线 与这个圆相交,此时这条直线 叫做圆的割线,A、B叫交点
?
?
小结:直线与圆的位置关系只有 相离、相切、相交三种
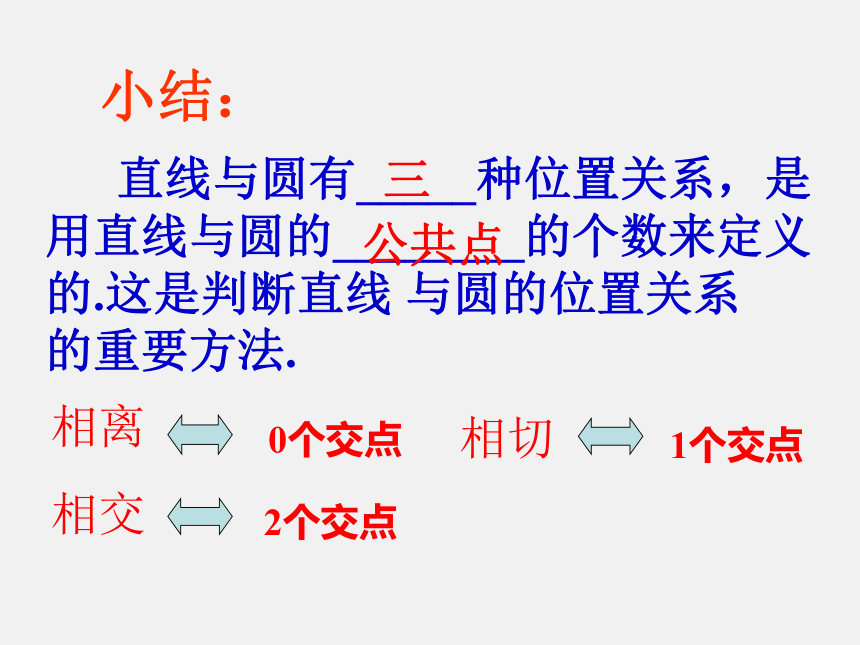
小结:
直线与圆有_____种位置关系,是
用直线与圆的________的个数来定义
的.这是判断直线 与圆的位置关系
的重要方法.
三
公共点
相离
0个交点
相切
1个交点
相交
2个交点
设圆O的半径为r,圆心O到直线l的距离为d,利用d与r之间的关系可以判断直线与圆的位置关系吗?
相离
d>r
相切
d=r
相交
d由上面的探索,你知道可以用哪些方法来判断直线与圆的位置关系?
直线与圆的位置关系可以用两种方法来判断:①看公共点的个数②用圆心到直线的距离d与半径r的大小比较
直线与圆的位置关系
d归纳与小结
d=r
d>r
2
交点
割线
1
切点
切线
0
直线与圆的位置关系 相交 相切 相离
公共点个数
公共点名称
直线名称
图 形
圆心到直线距离d与半径r的关系
1.直线与圆最多有两个公共点. ( )
2.若直线与圆相交,则直线上的点都在
圆内. ( )
3.若A、B是⊙O外两点,则直线AB与⊙O
相离. ( )
4 .若C为⊙O内与O点不重合的一点,则直线
CO与⊙O相交.( )
√
×
×
√
一、判断
二、填空:
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____,直线a与⊙O的公共点个数是____.
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _.
相交
相切
两个
3、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____.
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _.
零
相离
例 在Rt?ABC中 , ?C=90°, AC=3cm, BC=4cm , 以C为圆心, r 为半径的圆与AB有怎样的位置关系?为什么?
(1) r =2cm ; (2) r =2.4cm ;
(3) r =3cm.
A
B
C
A
B
D
C
D
B
C
A
C
B
D
(1) 当 r = 2cm时, 有 CD > r, 因此⊙C和AB相离.
(2) 当 r = 2.4cm时, 有 CD = r, 因此⊙C和AB相切.
(3) 当 r = 3cm时, 有 CD < r, 因此⊙C和AB相离.
解:在Rt△ABC中, BC=3,AC=4
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆.
想一想?
当r满足________________________时,⊙C与线段AB只有一个公共点.
r=2.4cm或 3cm.
A
B
C
A
B
C
随堂检测
1. ⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l 与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
判断:若线段和圆没有公共点,该圆圆心到线段的距离大于半径. ( )
A
C
×
4.判断:若直线和圆相切,则该直线和圆一定有一个公共点. ( )
√
5、在等腰△ABC中,AB=AC=2cm,若以A为圆心,1cm为半径的圆与BC相切,则∠BAC的度数为多少?( )
A、30°B、60°C、90°D、120°
解:过A点作AD⊥BC于D,
∵⊙O与BC相切,AD⊥BC
∴AD=⊙O的半径 =1cm,
在Rt△ABD中∠ADB=90°
∵BC= AD
∴∠ABC=30°∠BAC=120°
D
.
A
C
B
D
直线与圆的位置关系
1.理解直线与圆相交、相切、相离的概念.
学习目标
2.会根据圆心到直线的距离与半径的大小关系,判断直线与圆的位置关系.
大家看日出时,在太阳升起过程中,太阳与地平线有什么关系?
直线与圆有什么位置关系?
相离:
如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离
直线与圆有什么位置关系?
相离:
如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离
这时直线
与圆有什么关系?
相切:
如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相切,此时这条直线 叫圆的切线,这个公共点叫做切点.
?
P
A
B
这时直线
与圆有什么关系?
相交:
如果一条直线与一个圆有两个公共点,那么就说这条直线 与这个圆相交,此时这条直线 叫做圆的割线,A、B叫交点
?
?
小结:直线与圆的位置关系只有 相离、相切、相交三种
小结:
直线与圆有_____种位置关系,是
用直线与圆的________的个数来定义
的.这是判断直线 与圆的位置关系
的重要方法.
三
公共点
相离
0个交点
相切
1个交点
相交
2个交点
设圆O的半径为r,圆心O到直线l的距离为d,利用d与r之间的关系可以判断直线与圆的位置关系吗?
相离
d>r
相切
d=r
相交
d
直线与圆的位置关系可以用两种方法来判断:①看公共点的个数②用圆心到直线的距离d与半径r的大小比较
直线与圆的位置关系
d
d=r
d>r
2
交点
割线
1
切点
切线
0
直线与圆的位置关系 相交 相切 相离
公共点个数
公共点名称
直线名称
图 形
圆心到直线距离d与半径r的关系
1.直线与圆最多有两个公共点. ( )
2.若直线与圆相交,则直线上的点都在
圆内. ( )
3.若A、B是⊙O外两点,则直线AB与⊙O
相离. ( )
4 .若C为⊙O内与O点不重合的一点,则直线
CO与⊙O相交.( )
√
×
×
√
一、判断
二、填空:
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____,直线a与⊙O的公共点个数是____.
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _.
相交
相切
两个
3、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____.
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _.
零
相离
例 在Rt?ABC中 , ?C=90°, AC=3cm, BC=4cm , 以C为圆心, r 为半径的圆与AB有怎样的位置关系?为什么?
(1) r =2cm ; (2) r =2.4cm ;
(3) r =3cm.
A
B
C
A
B
D
C
D
B
C
A
C
B
D
(1) 当 r = 2cm时, 有 CD > r, 因此⊙C和AB相离.
(2) 当 r = 2.4cm时, 有 CD = r, 因此⊙C和AB相切.
(3) 当 r = 3cm时, 有 CD < r, 因此⊙C和AB相离.
解:在Rt△ABC中, BC=3,AC=4
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆.
想一想?
当r满足________________________时,⊙C与线段AB只有一个公共点.
r=2.4cm或 3cm
A
B
C
A
B
C
随堂检测
1. ⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l 与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
判断:若线段和圆没有公共点,该圆圆心到线段的距离大于半径. ( )
A
C
×
4.判断:若直线和圆相切,则该直线和圆一定有一个公共点. ( )
√
5、在等腰△ABC中,AB=AC=2cm,若以A为圆心,1cm为半径的圆与BC相切,则∠BAC的度数为多少?( )
A、30°B、60°C、90°D、120°
解:过A点作AD⊥BC于D,
∵⊙O与BC相切,AD⊥BC
∴AD=⊙O的半径 =1cm,
在Rt△ABD中∠ADB=90°
∵BC= AD
∴∠ABC=30°∠BAC=120°
D
.
A
C
B
D
