人教版五年级数学上册 5—2等式的基本性质和解方程 一课一练 精讲精练+奥数培优(无答案)
文档属性
| 名称 | 人教版五年级数学上册 5—2等式的基本性质和解方程 一课一练 精讲精练+奥数培优(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 22:31:37 | ||
图片预览



文档简介
等式的基本性质和解方程
知识引入:
一、等式的性质
例题1:
1.填空。
(1)4个苹果的质量+20 g砝码的质量=5个梨的质量+20 g砝码的质量4个苹果的质量=( )个梨的质量
(2)2只鸡的质量=4条鱼的质量,2条鱼的质量 =6个足球的质量,1只鸡的质量=( )个足球的质量
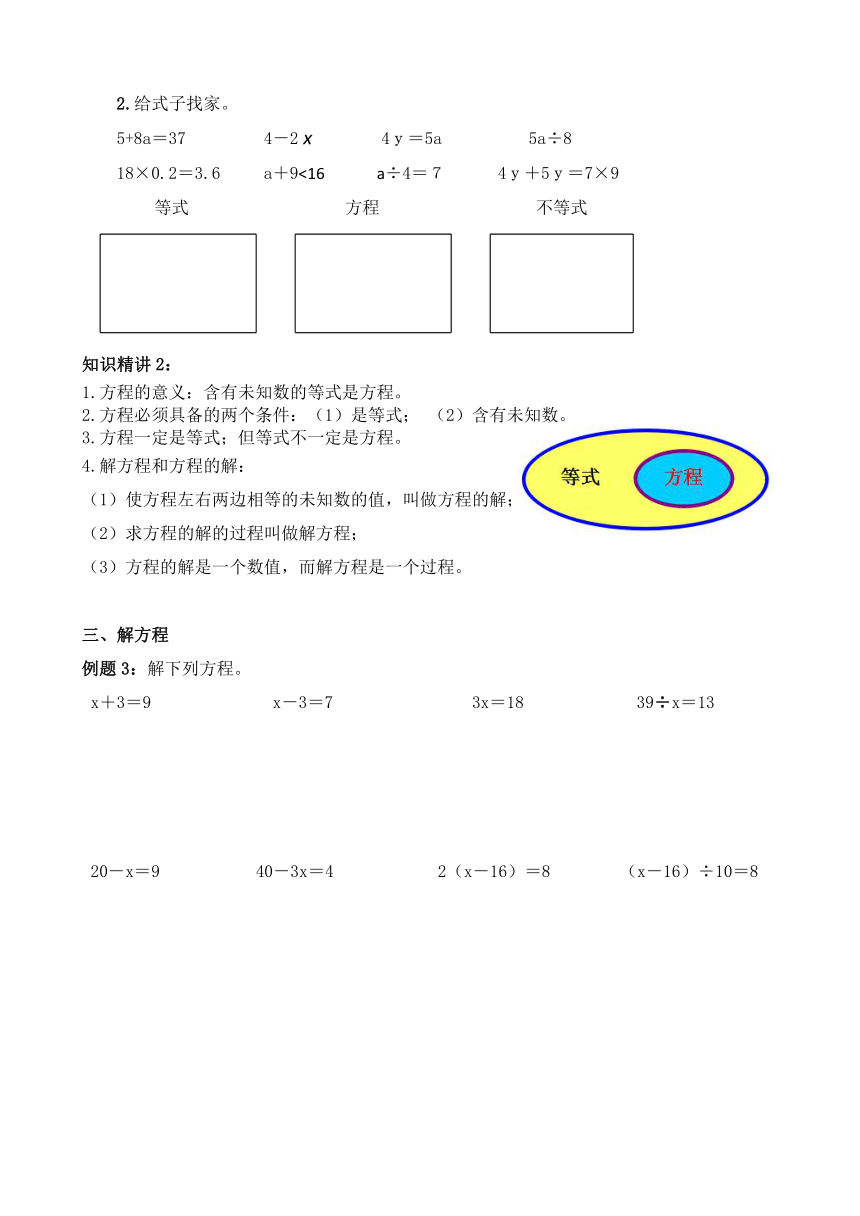
2.在括号里填上适当的符号和数,使天平平衡。
知识精讲1:等式的性质
(1)等式的性质1: 等式的两边同时加上或减去同一个数,左右两边仍然相等。
(2)等式的性质2:等式的两边同时乘或除以同一个不为0的数,左右两边仍然相等。
二、方程的意义
例题2:
1.判断。
(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程。 ( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )
2.给式子找家。
5+8a=37 4-2 x 4y=5a 5a÷8
18×0.2=3.6 a+9<16 a÷4=7 4y+5y=7×9
等式 方程 不等式
知识精讲2:
1.方程的意义:含有未知数的等式是方程。
2.方程必须具备的两个条件:(1)是等式; (2)含有未知数。
3.方程一定是等式;但等式不一定是方程。
4.解方程和方程的解:
(1)使方程左右两边相等的未知数的值,叫做方程的解;
(2)求方程的解的过程叫做解方程;
(3)方程的解是一个数值,而解方程是一个过程。
三、解方程
例题3:解下列方程。
x+3=9 x-3=7 3x=18 39÷x=13
20-x=9 40-3x=4 2(x-16)=8 (x-16)÷10=8
知识精讲3:
解方程的方法
(1)形如x+a=b的方程的解法:
①先写“解:”;
②在方程的两边同时减去a,使等式成立;
③求出x的值。
④将所求结果代入方程的左边,检验所求是否是方程的解。
(2)形如x-a=b的方程的解法:
①先写“解:”;
②在方程的两边同时加上a,使等式成立;
③求出x的值;
④将所求结果代入方程的左边,检验所求是否是方程的解。
(3)形如ax=b的方程的解法:
①写上“解:”;
②方程的两边同时除以a;
③计算出方程的解;
④将所求结果代入方程的左边,检验所求是否是方程的解。
(4)形如a÷x=b的方程的解法:
①写上“解:”;
②方程的两边同时乘以x;
③将方程的左右两边调换位置;
③计算出方程的解;
④将所求结果代入方程的左边,检验所求是否是方程的解。
(5)形如a-x=b的方程的解法:
①写上“解:”;
②方程的两边同时加上x;
③将方程的左右两边调换位置;
④计算出方程的解;
⑤将所求结果代入方程的左边,检验所求是否是方程的解。
(6)形如ax±b=c的方程的解法:
①写出“解:”;
②把ax看作一个整体,在方程的两边同时减去或加上b;
③计算出ax的结果;
④方程的两边同时除以a;
⑤计算出未知数x的值;
⑥检验。
(7)形如a(x±b)=c的方程的解法:
方法一:把小括号里的x±b看作一个整体,
先求出x±b的值,再求出x的值。
方法二:根据乘法分配律,
把a(x±b)=c转化成x±ab=c的方程,
求出ax的值,再求出x的值。
(8)形如(x±b)÷a=c的方程的解法:
方法一:把小括号里的x±b看作一个整体,
先求出x±b的值,再求出x的值。
方法二:根据乘法分配律,
把(x±b)÷a=c转化成(x±b)÷a×a=c×a,
得到x±b=c×a形式的方程,
求出ax的值,再求出x的值。
巩固练习:
一、填空。
1.如果苹果每千克a元,雪梨每千克b元,那么:
(1)4a表示( );
(2)2b表示( );
a-b表示( );
5(a+b)表示( );
若妈妈买了3千克苹果,2千克雪梨,共花28元钱。你能列出正确的方程吗?正确的
答案是( )。
2.牧场里有黄牛x头,奶牛的头数比黄牛的3倍少5头,奶牛有( )头,两种牛共有( )头。
3.甲袋有A千克面粉,乙袋有B千克面粉,如果从乙袋取出6千克放入甲袋中,甲、乙两袋
重量相等。列出等式是( )。
4.在①6+x=15,②9+8>14,③3.5a=14,④x-2.6,⑤y-8=10,⑥45+x<100,⑦74-28=46中,是等式的有( ),是方程的有( )(填序号)。
5.如果x+8=10.那么x=10-( );如果4x=3x+7,那么4x-( )=7。
6.天平一端放着一块巧克力,另一端放着半块巧克力和50克砝码,这时天平恰好平衡,整块巧克力重( )克。
7.如果x+3=8,那么x+3-3=8一( )。
8.根据图a和图b,可以判断图c中的天平( )端下沉。(填“左”或“右”)
二、判断。
1.方程一定是等式,而等式不一定是方程。 ( )
2.等式两边同时乘或除以一个相同的数,所得的结果仍是一个等式。 ( )
3.含有未知数的式子叫方程。 ( )
4.a、b都是不为O的自然数,已知a×2=b÷3,则a<b。 ( )
5.因为6=3+3.所以6×a=3+3×a。 ( )
6.(a+5)×2.2和2.2a+11相等。 ( )
7.当a=3时,a3和3a相等。 ( )
8.y=0不是方程。 ( )
9.3x+12是方程。 ( )
10.因为6×x=6x,所以6×7=6.7。 ( )
三、选择。
1.小明在解方程4x÷2=6时,是这样转化的:4x÷2×2=6×2,4x=12。他这样转化的依据是( )
A.被除数=除数×商 B.商不变的性质 C.等式的基本性质
2.等式两边都除以( )数,所得的结果仍然相等。
A.任何 B.同一个 C.同一个不为0的
3.甲数÷0.99=乙数×0.99(甲、乙两数均不为O),那么( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
4.用乘法分配律可以把“ab+a”改写成( )
A.(a+b)a B.(b+1)a C.b(a+a) D.(b+0)a
5.小勇今年a岁,爸爸今年b岁,爸爸比小勇大k岁,m年后,爸爸比小勇大多少岁?可列出等式( )
A. a-b=k B.b-a=k+m C.b-a=k D.b-a=m
6.学校书法组有168人,比美术组的2倍多20人,美术组有多少人?解:设美术组有x人。下列方程正确的是( )
A.2x-20=168 B.168-2x=20 C.2x-168=20
五、看图列方程。
(1) (2) (2)
(3) (4) (6)
六、趣味提升。
1.请给天平放上合适的砝码,使天平保持平衡。 (连线)
2.要使下图中的竹竿保持平衡.可以在竹竿右边的哪个地方放几个小方块?请你在图中画出来。
奥数思维拓展:
(一)同解方程
1.渗透一种数学思想:等量代换。
2.学习一类思维方法:分析法。
[例题]方程 x-0.8=2.4与mx=9.6有相同的解,求m的值。
[分析]
两个方程的解相同,也就是x的值相同,因此先求出 x-0.8=2.4的解,再把它带入mx=9.6中,会得到一个含有未知数m的新方程,求出这个方程的解,就是m的值。
[解答]
x-0.8=2.4 3.2m=9.6
解: x-0.8+0.8=2.4+0.8 3.2m÷3.2=9.6÷3.2
x =3.2 m=3
把 x =3.2带入mx=9.6中,得到3.2m=9.6。 答:m的值是3。
[技巧]
方程中虽然有两个未知数,但其中一个未知数的值隐含在已知条件中,通过计算可以先求出来,再把求出来的数值带入方程中,就可以求出另一个未知数。
举一反三:
1.方程x-0.6=5.4 与a÷x=0.6有相同的解,a是多少?
2.方程6÷x=4与bx=9有相同的解,b是多少?
3.方程c-x=4.5与d+x=2.5有相同的解,求c+d。
解复杂的方程
1.渗透两种数学思想:方程、转化。
2.学习一类思维方法:分析法。
[例题]解方程:7x+8x-13=17
[解答]
7x+8x-13=17
解:15x-13=17
15x=30
x=2
[技巧]观察方程,将能够先计算的部分先计算,使其简化,在求出x的值。
举一反三
1.解方程。
9.5x-6.1x+1.8=12 4x+0.7x-2x+1.9=10
2.解方程: 8x-7=2.5x+20.5。
知识引入:
一、等式的性质
例题1:
1.填空。
(1)4个苹果的质量+20 g砝码的质量=5个梨的质量+20 g砝码的质量4个苹果的质量=( )个梨的质量
(2)2只鸡的质量=4条鱼的质量,2条鱼的质量 =6个足球的质量,1只鸡的质量=( )个足球的质量
2.在括号里填上适当的符号和数,使天平平衡。
知识精讲1:等式的性质
(1)等式的性质1: 等式的两边同时加上或减去同一个数,左右两边仍然相等。
(2)等式的性质2:等式的两边同时乘或除以同一个不为0的数,左右两边仍然相等。
二、方程的意义
例题2:
1.判断。
(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程。 ( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )
2.给式子找家。
5+8a=37 4-2 x 4y=5a 5a÷8
18×0.2=3.6 a+9<16 a÷4=7 4y+5y=7×9
等式 方程 不等式
知识精讲2:
1.方程的意义:含有未知数的等式是方程。
2.方程必须具备的两个条件:(1)是等式; (2)含有未知数。
3.方程一定是等式;但等式不一定是方程。
4.解方程和方程的解:
(1)使方程左右两边相等的未知数的值,叫做方程的解;
(2)求方程的解的过程叫做解方程;
(3)方程的解是一个数值,而解方程是一个过程。
三、解方程
例题3:解下列方程。
x+3=9 x-3=7 3x=18 39÷x=13
20-x=9 40-3x=4 2(x-16)=8 (x-16)÷10=8
知识精讲3:
解方程的方法
(1)形如x+a=b的方程的解法:
①先写“解:”;
②在方程的两边同时减去a,使等式成立;
③求出x的值。
④将所求结果代入方程的左边,检验所求是否是方程的解。
(2)形如x-a=b的方程的解法:
①先写“解:”;
②在方程的两边同时加上a,使等式成立;
③求出x的值;
④将所求结果代入方程的左边,检验所求是否是方程的解。
(3)形如ax=b的方程的解法:
①写上“解:”;
②方程的两边同时除以a;
③计算出方程的解;
④将所求结果代入方程的左边,检验所求是否是方程的解。
(4)形如a÷x=b的方程的解法:
①写上“解:”;
②方程的两边同时乘以x;
③将方程的左右两边调换位置;
③计算出方程的解;
④将所求结果代入方程的左边,检验所求是否是方程的解。
(5)形如a-x=b的方程的解法:
①写上“解:”;
②方程的两边同时加上x;
③将方程的左右两边调换位置;
④计算出方程的解;
⑤将所求结果代入方程的左边,检验所求是否是方程的解。
(6)形如ax±b=c的方程的解法:
①写出“解:”;
②把ax看作一个整体,在方程的两边同时减去或加上b;
③计算出ax的结果;
④方程的两边同时除以a;
⑤计算出未知数x的值;
⑥检验。
(7)形如a(x±b)=c的方程的解法:
方法一:把小括号里的x±b看作一个整体,
先求出x±b的值,再求出x的值。
方法二:根据乘法分配律,
把a(x±b)=c转化成x±ab=c的方程,
求出ax的值,再求出x的值。
(8)形如(x±b)÷a=c的方程的解法:
方法一:把小括号里的x±b看作一个整体,
先求出x±b的值,再求出x的值。
方法二:根据乘法分配律,
把(x±b)÷a=c转化成(x±b)÷a×a=c×a,
得到x±b=c×a形式的方程,
求出ax的值,再求出x的值。
巩固练习:
一、填空。
1.如果苹果每千克a元,雪梨每千克b元,那么:
(1)4a表示( );
(2)2b表示( );
a-b表示( );
5(a+b)表示( );
若妈妈买了3千克苹果,2千克雪梨,共花28元钱。你能列出正确的方程吗?正确的
答案是( )。
2.牧场里有黄牛x头,奶牛的头数比黄牛的3倍少5头,奶牛有( )头,两种牛共有( )头。
3.甲袋有A千克面粉,乙袋有B千克面粉,如果从乙袋取出6千克放入甲袋中,甲、乙两袋
重量相等。列出等式是( )。
4.在①6+x=15,②9+8>14,③3.5a=14,④x-2.6,⑤y-8=10,⑥45+x<100,⑦74-28=46中,是等式的有( ),是方程的有( )(填序号)。
5.如果x+8=10.那么x=10-( );如果4x=3x+7,那么4x-( )=7。
6.天平一端放着一块巧克力,另一端放着半块巧克力和50克砝码,这时天平恰好平衡,整块巧克力重( )克。
7.如果x+3=8,那么x+3-3=8一( )。
8.根据图a和图b,可以判断图c中的天平( )端下沉。(填“左”或“右”)
二、判断。
1.方程一定是等式,而等式不一定是方程。 ( )
2.等式两边同时乘或除以一个相同的数,所得的结果仍是一个等式。 ( )
3.含有未知数的式子叫方程。 ( )
4.a、b都是不为O的自然数,已知a×2=b÷3,则a<b。 ( )
5.因为6=3+3.所以6×a=3+3×a。 ( )
6.(a+5)×2.2和2.2a+11相等。 ( )
7.当a=3时,a3和3a相等。 ( )
8.y=0不是方程。 ( )
9.3x+12是方程。 ( )
10.因为6×x=6x,所以6×7=6.7。 ( )
三、选择。
1.小明在解方程4x÷2=6时,是这样转化的:4x÷2×2=6×2,4x=12。他这样转化的依据是( )
A.被除数=除数×商 B.商不变的性质 C.等式的基本性质
2.等式两边都除以( )数,所得的结果仍然相等。
A.任何 B.同一个 C.同一个不为0的
3.甲数÷0.99=乙数×0.99(甲、乙两数均不为O),那么( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
4.用乘法分配律可以把“ab+a”改写成( )
A.(a+b)a B.(b+1)a C.b(a+a) D.(b+0)a
5.小勇今年a岁,爸爸今年b岁,爸爸比小勇大k岁,m年后,爸爸比小勇大多少岁?可列出等式( )
A. a-b=k B.b-a=k+m C.b-a=k D.b-a=m
6.学校书法组有168人,比美术组的2倍多20人,美术组有多少人?解:设美术组有x人。下列方程正确的是( )
A.2x-20=168 B.168-2x=20 C.2x-168=20
五、看图列方程。
(1) (2) (2)
(3) (4) (6)
六、趣味提升。
1.请给天平放上合适的砝码,使天平保持平衡。 (连线)
2.要使下图中的竹竿保持平衡.可以在竹竿右边的哪个地方放几个小方块?请你在图中画出来。
奥数思维拓展:
(一)同解方程
1.渗透一种数学思想:等量代换。
2.学习一类思维方法:分析法。
[例题]方程 x-0.8=2.4与mx=9.6有相同的解,求m的值。
[分析]
两个方程的解相同,也就是x的值相同,因此先求出 x-0.8=2.4的解,再把它带入mx=9.6中,会得到一个含有未知数m的新方程,求出这个方程的解,就是m的值。
[解答]
x-0.8=2.4 3.2m=9.6
解: x-0.8+0.8=2.4+0.8 3.2m÷3.2=9.6÷3.2
x =3.2 m=3
把 x =3.2带入mx=9.6中,得到3.2m=9.6。 答:m的值是3。
[技巧]
方程中虽然有两个未知数,但其中一个未知数的值隐含在已知条件中,通过计算可以先求出来,再把求出来的数值带入方程中,就可以求出另一个未知数。
举一反三:
1.方程x-0.6=5.4 与a÷x=0.6有相同的解,a是多少?
2.方程6÷x=4与bx=9有相同的解,b是多少?
3.方程c-x=4.5与d+x=2.5有相同的解,求c+d。
解复杂的方程
1.渗透两种数学思想:方程、转化。
2.学习一类思维方法:分析法。
[例题]解方程:7x+8x-13=17
[解答]
7x+8x-13=17
解:15x-13=17
15x=30
x=2
[技巧]观察方程,将能够先计算的部分先计算,使其简化,在求出x的值。
举一反三
1.解方程。
9.5x-6.1x+1.8=12 4x+0.7x-2x+1.9=10
2.解方程: 8x-7=2.5x+20.5。
