人教A版高中数学必修五2.4.1等比数列的概念及通项公式 课件(共34张PPT)
文档属性
| 名称 | 人教A版高中数学必修五2.4.1等比数列的概念及通项公式 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 22:38:12 | ||
图片预览









文档简介
(共34张PPT)
自律成就人生
网课结束日,学校见面时。
真学与假学,一测便知晓!
第1课时 等比数列的概念及通项公式
复习回顾
等差数列
概念
通项公式
求和公式
相关性质
最值问题
带绝对值求和
实际问题
学习目标
XUEXIMUBIAO
1.通过实例,理解等比数列的概念.
2.掌握等比中项的概念并会应用.
3.掌握等比数列的通项公式并了解其推导过程.
共同特点:
从第二项起,每一项与其前一项的比是同一个常数
对于数列①,从第2项起,每一项与前一项的比都等于__;
①
②
③
对于数列②,从第2项起,每一项与前一项的比都等于__;
对于数列①,从第2项起,每一项与前一项的比都等于__;
类比“等差数列”,这样的数列可以叫做“等比数列”。
引导探究,掌握新知
请问:这三个数列有什么共同特点?
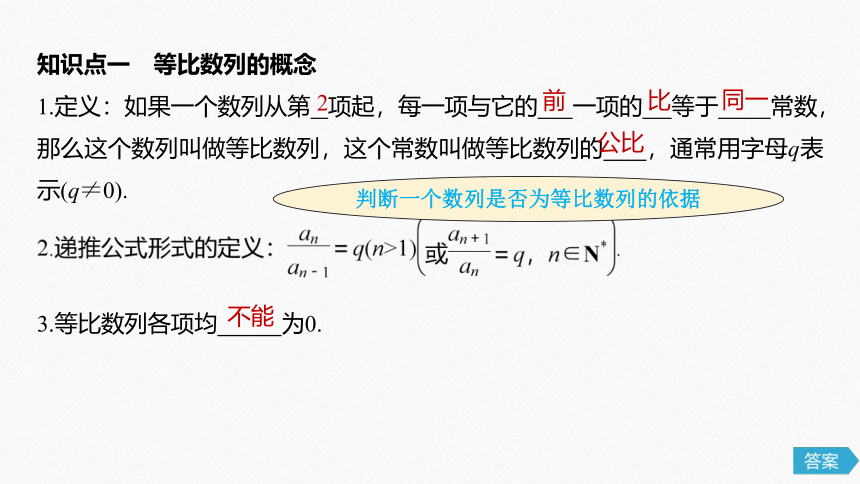
知识点一 等比数列的概念
1.定义:如果一个数列从第 项起,每一项与它的 一项的 等于 常数,那么这个数列叫做等比数列,这个常数叫做等比数列的 ,通常用字母q表示(q≠0).
3.等比数列各项均 为0.
2
前
比
同一
公比
不能
判断一个数列是否为等比数列的依据
知识点二 等比中项与等差中项的异同
对比项 等差中项 等比中项
定义 若a,A,b成等差数列,则A叫做a与b的等差中项 若a,G,b成 数列,则G叫做a与b的 中项
定义式 A-a=b-A
公式 A= G=±
个数 a与b的等差中项唯一 a与b的等比中项有 个,且互为__
____
备注 任意两个数a与b都有等差中项 只有当ab>0时,a与b才有等比中项
等比
等比
两
相
反数
… …
1
1
-
=
n
n
q
a
a
… …
类比
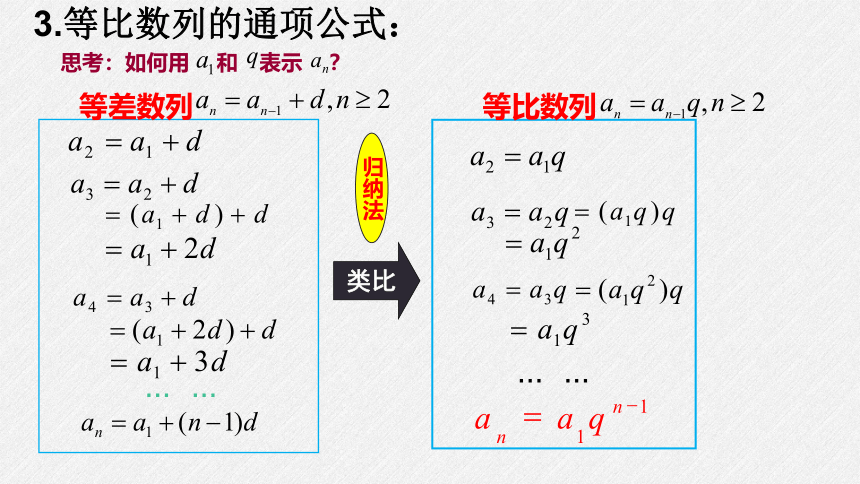
3.等比数列的通项公式:
等差数列
等比数列
归纳法
思考:如何用 和 表示 ?
累乘法
……
共n – 1 项
×)
等比数列
方法:累加法
……
+)
等差数列
类比
思考:如何用 和 表示 ?
3.等比数列的通项公式:
等比数列 名称 等差数列
概念
常数
定义式
通项公式
中项
公式
从第2项起,每一项与它前一项的比等同一个非零常数
从第2项起,每一项与它前一项的差等同一个常数
或
公比
公差
类 比
1.若an+1=qan,n∈N*,且q≠0,则{an}是等比数列.( )
2.任何两个数都有等比中项.( )
思考辨析 判断正误
SIKAOBIANXIPANDUANZHENGWU
√
4.常数列既是等差数列,又是等比数列.( )
×
×
×
2
题型探究
PART TWO
题型一 等比数列的判定
命题角度1 已知数列前若干项判断是否为等比数列
例1 判断下列数列是否为等比数列.
(1)1,3,32,33,…,3n-1,…;
多维探究
解 记数列为{an},显然a1=1,a2=3,…,an=3n-1,….
∴数列为等比数列,且公比为3.
(2)-1,1,2,4,8,…;
解 记数列为{an},显然a1=-1,a2=1,a3=2,…,
∴此数列不是等比数列.
(3)a1,a2,a3,…,an,….
解 当a=0时,数列为0,0,0,…是常数列,不是等比数列;
当a≠0时,数列为a1,a2,a3,a4,…,an,…,
显然此数列为等比数列,且公比为a.
反思感悟 判定等比数列,要抓住3个要点:
①从第二项起.②要判定每一项,不能有例外.③每一项与前一项的比是同一个常数,且不能为0.
跟踪训练1 下列各组数成等比数列的是
A.①② B.①②③ C.①②④ D.①②③④
√
解析 ①②显然是等比数列;
由于x可能为0,③不是;
a不能为0,④符合等比数列定义,故④是.
命题角度2 已知递推公式判断是否为等比数列
例2 已知数列{an}满足a1=1,an+1=2an+1.
(1)证明:数列{an+1}是等比数列;
证明 ∵an+1=2an+1,∴an+1+1=2(an+1).由a1=1,知a1+1≠0,从而an+1≠0.
∴数列{an+1}是等比数列.
(2)求数列{an}的通项公式.
解 由(1)知{an+1}是以a1+1=2为首项,2为公比的等比数列.
∴an+1=2·2n-1=2n.
即an=2n-1.
反思感悟 等比数列的判定方法
跟踪训练2 数列{an}满足a1=-1,且an=3an-1-2n+3(n=2,3,…).
(1)求a2,a3,并证明数列{an-n}是等比数列;
解 a2=3a1-2×2+3=-4,a3=3a2-2×3+3=-15.
又a1-1=-2,
∴数列{an-n}是以-2为首项,3为公比的等比数列.
(2)求数列{an}的通项公式.
解 由(1)知an-n=-2·3n-1,∴an=n-2·3n-1.
题型二 等比数列通项公式的应用
例3 在等比数列{an}中.
解 设等比数列{an}的公比为q.
反思感悟 等比数列通项公式及应用应注意两点
(1)a1和q是等比数列的基本元素,只要求出这两个基本元素,其余的元素便可求出.
(2)等比数列的通项公式涉及4个量a1,an,n,q,知任意三个就可以求出另外一个.
跟踪训练3 在等比数列{an}中:
(1)已知a1=3,q=-2,求a6;
解 由等比数列的通项公式得,a6=3×(-2)6-1=-96.
(2)已知a3=20,a6=160,求an.
解 设等比数列的公比为q,
所以an=a1qn-1=5×2n-1,n∈N*.
题型三:等比中项的应用
例4
跟踪训练4
A.5√2 B.7 C.6 D.4√2
A
3
达标检测
PART THREE
1
2
3
4
5
1.等比数列{an}的公比|q|>1,{an}中有连续四项在集合{-54,-24,-18,
36,81}中.则q等于
√
解析 ∵{an}中的项必然有正有负,
∴q<0.又|q|>1,
∴{|an|}递增或递减.
由此可得{an}的连续四项为-24,36,-54,81.
1
2
3
4
5
2.等比数列x,3x+3,6x+6,…的第4项等于
A.-24 B.0 C.12 D.24
√
解析 由题意知(3x+3)2=x(6x+6),即x2+4x+3=0,
解得x=-3或x=-1(舍去),
所以等比数列的前3项是-3,-6,-12,
则第4项为-24.
1
2
3
4
5
3.若等比数列的首项为4,末项为128,公比为2,则这个数列的项数为
A.4 B.8 C.6 D.32
√
解析 由等比数列的通项公式得,128=4×2n-1,2n-1=32,
所以n=6.
1
2
3
4
5
4. 45和80的等比中项为 .
-60或60
解析 设45和80的等比中项为G,
则G2=45×80,∴G=±60.
1
2
3
4
5
5.若{an}为等比数列,且3a4=a6-2a5,则公比是 .
-1或3
解析 设公比为q(q≠0),则3a1q3=a1q5-2a1q4,
因为a1q3≠0,所以q2-2q-3=0,
解得q=-1或q=3.
课堂小结
KETANGXIAOJIE
1.等比数列的判断或证明
3.等比数列的通项公式an=a1qn-1共涉及a1,q,n,an四个量,已知其中三个量可求得第四个量.
思考:等比数列的公比与该数列的类型有关系吗?
知识点四 等比数列的类型
(1)数列:1,2,4,8,16,…
(2)数列:
(5)数列:4,4,4,4,4,4,4,…
(3)数列:-1,-2,-4,-8,-16,…
(4)数列:
(6)数列:-1,2,-4,8,-16,…
(7)数列:1,-2,4,-8,16,…
已知数列{an}是等比数列,q是公比,则:
q>1 0
递增
递减
常数列
递增
递减
a1<0
a1>0
摆动数列
知识点四 等比数列的类型
自律成就人生
网课结束日,学校见面时。
真学与假学,一测便知晓!
第1课时 等比数列的概念及通项公式
复习回顾
等差数列
概念
通项公式
求和公式
相关性质
最值问题
带绝对值求和
实际问题
学习目标
XUEXIMUBIAO
1.通过实例,理解等比数列的概念.
2.掌握等比中项的概念并会应用.
3.掌握等比数列的通项公式并了解其推导过程.
共同特点:
从第二项起,每一项与其前一项的比是同一个常数
对于数列①,从第2项起,每一项与前一项的比都等于__;
①
②
③
对于数列②,从第2项起,每一项与前一项的比都等于__;
对于数列①,从第2项起,每一项与前一项的比都等于__;
类比“等差数列”,这样的数列可以叫做“等比数列”。
引导探究,掌握新知
请问:这三个数列有什么共同特点?
知识点一 等比数列的概念
1.定义:如果一个数列从第 项起,每一项与它的 一项的 等于 常数,那么这个数列叫做等比数列,这个常数叫做等比数列的 ,通常用字母q表示(q≠0).
3.等比数列各项均 为0.
2
前
比
同一
公比
不能
判断一个数列是否为等比数列的依据
知识点二 等比中项与等差中项的异同
对比项 等差中项 等比中项
定义 若a,A,b成等差数列,则A叫做a与b的等差中项 若a,G,b成 数列,则G叫做a与b的 中项
定义式 A-a=b-A
公式 A= G=±
个数 a与b的等差中项唯一 a与b的等比中项有 个,且互为__
____
备注 任意两个数a与b都有等差中项 只有当ab>0时,a与b才有等比中项
等比
等比
两
相
反数
… …
1
1
-
=
n
n
q
a
a
… …
类比
3.等比数列的通项公式:
等差数列
等比数列
归纳法
思考:如何用 和 表示 ?
累乘法
……
共n – 1 项
×)
等比数列
方法:累加法
……
+)
等差数列
类比
思考:如何用 和 表示 ?
3.等比数列的通项公式:
等比数列 名称 等差数列
概念
常数
定义式
通项公式
中项
公式
从第2项起,每一项与它前一项的比等同一个非零常数
从第2项起,每一项与它前一项的差等同一个常数
或
公比
公差
类 比
1.若an+1=qan,n∈N*,且q≠0,则{an}是等比数列.( )
2.任何两个数都有等比中项.( )
思考辨析 判断正误
SIKAOBIANXIPANDUANZHENGWU
√
4.常数列既是等差数列,又是等比数列.( )
×
×
×
2
题型探究
PART TWO
题型一 等比数列的判定
命题角度1 已知数列前若干项判断是否为等比数列
例1 判断下列数列是否为等比数列.
(1)1,3,32,33,…,3n-1,…;
多维探究
解 记数列为{an},显然a1=1,a2=3,…,an=3n-1,….
∴数列为等比数列,且公比为3.
(2)-1,1,2,4,8,…;
解 记数列为{an},显然a1=-1,a2=1,a3=2,…,
∴此数列不是等比数列.
(3)a1,a2,a3,…,an,….
解 当a=0时,数列为0,0,0,…是常数列,不是等比数列;
当a≠0时,数列为a1,a2,a3,a4,…,an,…,
显然此数列为等比数列,且公比为a.
反思感悟 判定等比数列,要抓住3个要点:
①从第二项起.②要判定每一项,不能有例外.③每一项与前一项的比是同一个常数,且不能为0.
跟踪训练1 下列各组数成等比数列的是
A.①② B.①②③ C.①②④ D.①②③④
√
解析 ①②显然是等比数列;
由于x可能为0,③不是;
a不能为0,④符合等比数列定义,故④是.
命题角度2 已知递推公式判断是否为等比数列
例2 已知数列{an}满足a1=1,an+1=2an+1.
(1)证明:数列{an+1}是等比数列;
证明 ∵an+1=2an+1,∴an+1+1=2(an+1).由a1=1,知a1+1≠0,从而an+1≠0.
∴数列{an+1}是等比数列.
(2)求数列{an}的通项公式.
解 由(1)知{an+1}是以a1+1=2为首项,2为公比的等比数列.
∴an+1=2·2n-1=2n.
即an=2n-1.
反思感悟 等比数列的判定方法
跟踪训练2 数列{an}满足a1=-1,且an=3an-1-2n+3(n=2,3,…).
(1)求a2,a3,并证明数列{an-n}是等比数列;
解 a2=3a1-2×2+3=-4,a3=3a2-2×3+3=-15.
又a1-1=-2,
∴数列{an-n}是以-2为首项,3为公比的等比数列.
(2)求数列{an}的通项公式.
解 由(1)知an-n=-2·3n-1,∴an=n-2·3n-1.
题型二 等比数列通项公式的应用
例3 在等比数列{an}中.
解 设等比数列{an}的公比为q.
反思感悟 等比数列通项公式及应用应注意两点
(1)a1和q是等比数列的基本元素,只要求出这两个基本元素,其余的元素便可求出.
(2)等比数列的通项公式涉及4个量a1,an,n,q,知任意三个就可以求出另外一个.
跟踪训练3 在等比数列{an}中:
(1)已知a1=3,q=-2,求a6;
解 由等比数列的通项公式得,a6=3×(-2)6-1=-96.
(2)已知a3=20,a6=160,求an.
解 设等比数列的公比为q,
所以an=a1qn-1=5×2n-1,n∈N*.
题型三:等比中项的应用
例4
跟踪训练4
A.5√2 B.7 C.6 D.4√2
A
3
达标检测
PART THREE
1
2
3
4
5
1.等比数列{an}的公比|q|>1,{an}中有连续四项在集合{-54,-24,-18,
36,81}中.则q等于
√
解析 ∵{an}中的项必然有正有负,
∴q<0.又|q|>1,
∴{|an|}递增或递减.
由此可得{an}的连续四项为-24,36,-54,81.
1
2
3
4
5
2.等比数列x,3x+3,6x+6,…的第4项等于
A.-24 B.0 C.12 D.24
√
解析 由题意知(3x+3)2=x(6x+6),即x2+4x+3=0,
解得x=-3或x=-1(舍去),
所以等比数列的前3项是-3,-6,-12,
则第4项为-24.
1
2
3
4
5
3.若等比数列的首项为4,末项为128,公比为2,则这个数列的项数为
A.4 B.8 C.6 D.32
√
解析 由等比数列的通项公式得,128=4×2n-1,2n-1=32,
所以n=6.
1
2
3
4
5
4. 45和80的等比中项为 .
-60或60
解析 设45和80的等比中项为G,
则G2=45×80,∴G=±60.
1
2
3
4
5
5.若{an}为等比数列,且3a4=a6-2a5,则公比是 .
-1或3
解析 设公比为q(q≠0),则3a1q3=a1q5-2a1q4,
因为a1q3≠0,所以q2-2q-3=0,
解得q=-1或q=3.
课堂小结
KETANGXIAOJIE
1.等比数列的判断或证明
3.等比数列的通项公式an=a1qn-1共涉及a1,q,n,an四个量,已知其中三个量可求得第四个量.
思考:等比数列的公比与该数列的类型有关系吗?
知识点四 等比数列的类型
(1)数列:1,2,4,8,16,…
(2)数列:
(5)数列:4,4,4,4,4,4,4,…
(3)数列:-1,-2,-4,-8,-16,…
(4)数列:
(6)数列:-1,2,-4,8,-16,…
(7)数列:1,-2,4,-8,16,…
已知数列{an}是等比数列,q是公比,则:
q>1 0
递增
递减
常数列
递增
递减
a1<0
a1>0
摆动数列
知识点四 等比数列的类型
