人教版数学三下第8单元 数学广角——搭配(二)整理和复习 课件(21张)
文档属性
| 名称 | 人教版数学三下第8单元 数学广角——搭配(二)整理和复习 课件(21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 21:26:09 | ||
图片预览







文档简介
(共21张PPT)
第8单元整理和复习
例1 用 三张数字卡片能摆出多少个不同的三位数?
思路分析:可以用列举法,先摆出百位,再摆出十位和个位,但要注意0不能作百位。
用8作百位,则有860、806两种摆法;用6作百位,则有680、608两种摆法,所以共能摆出4个不同的三位数。
规范解答:
能摆出4个不同的三位数,860、806、680、608。
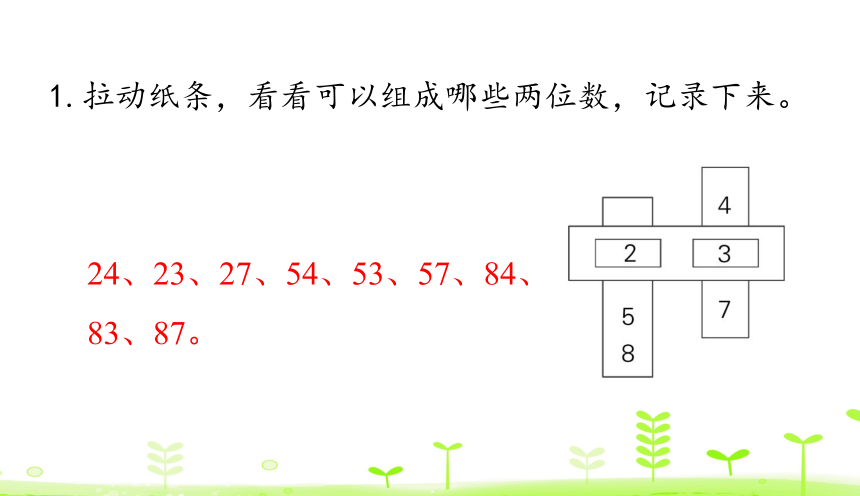
1.拉动纸条,看看可以组成哪些两位数,记录下来。
24、23、27、54、53、57、84、83、87。
例2 8名乒乓球运动员参加单打比赛,两两配对进行淘汰赛,要决出冠军,一共要比赛多少场?
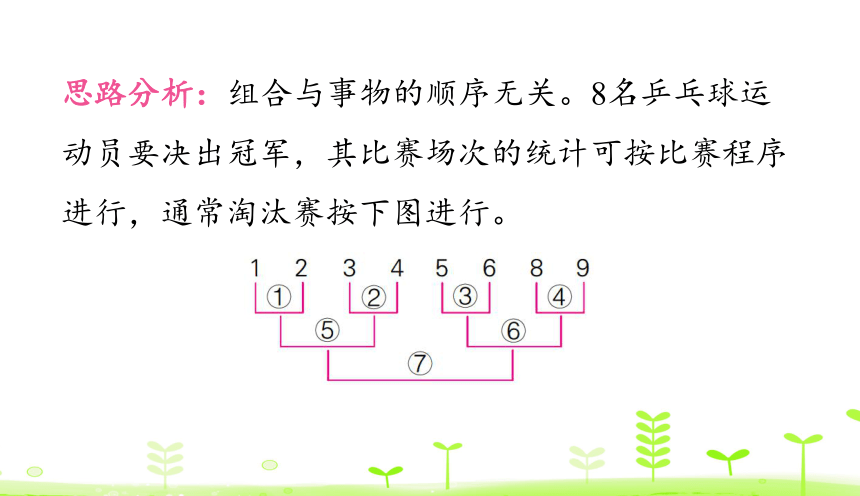
思路分析:组合与事物的顺序无关。8名乒乓球运动员要决出冠军,其比赛场次的统计可按比赛程序进行,通常淘汰赛按下图进行。
规范解答:4+2+1=7(场)
答:一共要比赛7场。
2.如下图,从甲地到乙地有2条路可走,从乙地到丙地有3条路可走,从甲地到丙地有4条路可走。从甲地到丙地共有多少种不同的走法?
2×3+4=10
答:共有10种不同的走法。
巩固练习
1.唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意换位置,一共有多少种坐法?
一共有6种坐法。
孙悟空 猪八戒 唐僧 沙和尚
2.用2、5、7、9组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
能组成9个个位是单数的两位数。
3.右面4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
这样的摆法一共有18种。
4.
一共要拍8张照片。
一共要拍多少张照片?
一共有9个长方形。
5.右图中一共有多少个长方形?
6.从鸟岛到狮虎山,共有多少条路线?
共有8条路线。
7.甲、乙、丙、丁4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛多少场?
一共要比赛6场。
8.
(1)小明想从中任选2本,共有多少种选法?
(2)小明想选《数学家的故事》和1本其他的书分别送给小红和小丽,共有多少种送法?
共有6种选法。
共有6种送法。
9.按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
(1)小于1而小数部分是三位的小数。
(2)大于7而小数部分是三位的小数。
0.567 0.576 0.657 0.675 0.765 0.756
7.056 7.065 7.506 7.560 7.605 7.650
10.从100到300的数中,有多少个十位和个位相同的数?
有21个十位和个位相同的数。
第8单元整理和复习
例1 用 三张数字卡片能摆出多少个不同的三位数?
思路分析:可以用列举法,先摆出百位,再摆出十位和个位,但要注意0不能作百位。
用8作百位,则有860、806两种摆法;用6作百位,则有680、608两种摆法,所以共能摆出4个不同的三位数。
规范解答:
能摆出4个不同的三位数,860、806、680、608。
1.拉动纸条,看看可以组成哪些两位数,记录下来。
24、23、27、54、53、57、84、83、87。
例2 8名乒乓球运动员参加单打比赛,两两配对进行淘汰赛,要决出冠军,一共要比赛多少场?
思路分析:组合与事物的顺序无关。8名乒乓球运动员要决出冠军,其比赛场次的统计可按比赛程序进行,通常淘汰赛按下图进行。
规范解答:4+2+1=7(场)
答:一共要比赛7场。
2.如下图,从甲地到乙地有2条路可走,从乙地到丙地有3条路可走,从甲地到丙地有4条路可走。从甲地到丙地共有多少种不同的走法?
2×3+4=10
答:共有10种不同的走法。
巩固练习
1.唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意换位置,一共有多少种坐法?
一共有6种坐法。
孙悟空 猪八戒 唐僧 沙和尚
2.用2、5、7、9组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
能组成9个个位是单数的两位数。
3.右面4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
这样的摆法一共有18种。
4.
一共要拍8张照片。
一共要拍多少张照片?
一共有9个长方形。
5.右图中一共有多少个长方形?
6.从鸟岛到狮虎山,共有多少条路线?
共有8条路线。
7.甲、乙、丙、丁4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛多少场?
一共要比赛6场。
8.
(1)小明想从中任选2本,共有多少种选法?
(2)小明想选《数学家的故事》和1本其他的书分别送给小红和小丽,共有多少种送法?
共有6种选法。
共有6种送法。
9.按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
(1)小于1而小数部分是三位的小数。
(2)大于7而小数部分是三位的小数。
0.567 0.576 0.657 0.675 0.765 0.756
7.056 7.065 7.506 7.560 7.605 7.650
10.从100到300的数中,有多少个十位和个位相同的数?
有21个十位和个位相同的数。
