2020年中考数学总复习课件:三角形与多边形(共61张PPT)
文档属性
| 名称 | 2020年中考数学总复习课件:三角形与多边形(共61张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览










文档简介
(共61张PPT)
三角形与多边形
第 * 页
首尾顺次
第 * 页
直
锐
钝
等边
第 * 页
2.三角形中的重要线段——三角形的角平分线、中线、高、中位线和中垂线
(1)三角形的角平分线.
概念:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点和交点的线段叫做三角形的⑥____________.
性质:Ⅰ.如图,若AD为△ABC的角平分线,则有∠BAD=∠CAD;
Ⅱ.三角形角平分线上的点到角两边的距离⑦________;
Ⅲ.三角形有三条角平分线,均在三角形的⑧________;
Ⅳ.三角形的三条角平分线交于一点,该点到三角形三边的距离均相等,称为三角形的⑨________.
角平分线
相等
内部
内心
第 * 页
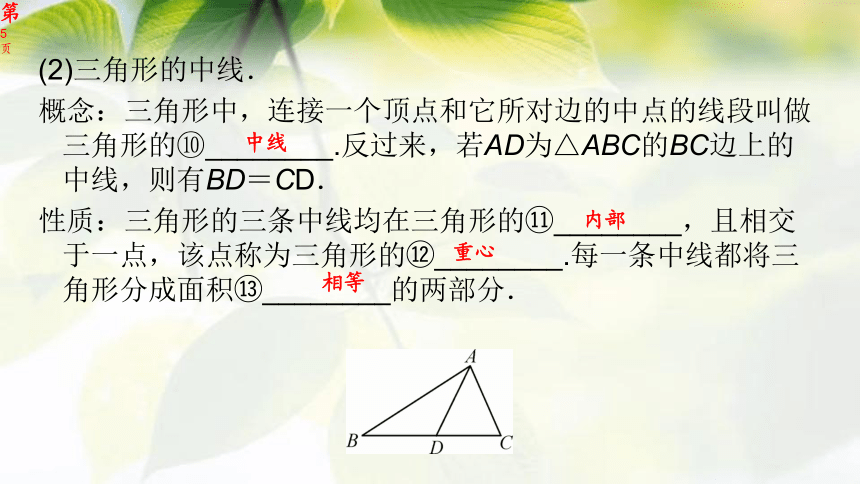
(2)三角形的中线.
概念:三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的⑩________.反过来,若AD为△ABC的BC边上的中线,则有BD=CD.
性质:三角形的三条中线均在三角形的?________,且相交于一点,该点称为三角形的?________.每一条中线都将三角形分成面积?________的两部分.
中线
内部
重心
相等
第 * 页
(3)三角形的高.
从三角形一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫做三角形这条边上的?______.
高
第 * 页
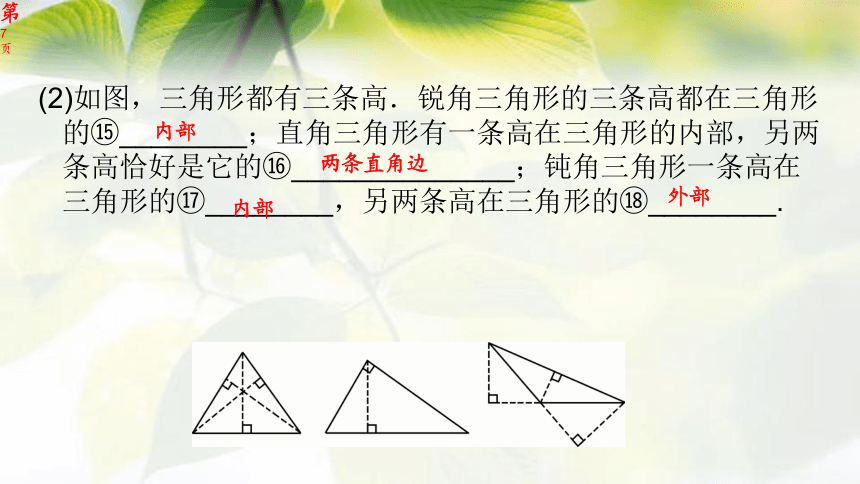
(2)如图,三角形都有三条高.锐角三角形的三条高都在三角形的?________;直角三角形有一条高在三角形的内部,另两条高恰好是它的?______________;钝角三角形一条高在三角形的?________,另两条高在三角形的?________.
内部
两条直角边
内部
外部
第 * 页
中点
平行
一半
第 * 页
(5)三角形的中垂线.
三角形的边的中垂线有时也叫三角形的中垂线.三角形中垂线的交点是三角形的外心,三角形的外心到三角形三个顶点的距离相等.
第 * 页
二 三角形的性质
1. 三角形的稳定性
定义:如果三角形三边的长度固定,那么三角形的形状和大小就能唯一确定下来.三角形的这个性质叫做三角形的稳定性.
应用:三角形的稳定性是三角形独有的性质,在现实生活中应用非常广泛.例如:大桥的钢架做成三角形、高压电线的支架做成三角形等.
第 * 页
大于
小于
第 * 页
180°
180°
第 * 页
等于
大于
第 * 页
360°
大角
小角
第 * 页
第 * 页
(2)凸多边形.
把一个多边形任意一边向两方无限延长成为一条直线,如果多边形的其余各边均在此直线的同旁,那么这个多边形就叫做凸多边形.例如:图1中的多边形ABCDE为凸多边形,图2中的多边形ABCDE不是凸多边形.
第 * 页
(n-2)×180°
360°
(n-3)
(n-2)
第 * 页
相等
相等
轴对称
n
中心对称
轴对称
n
第 * 页
相等
等边
第 * 页
等角
相等
重合
⊥
=
⊥
=
=
=
轴对称
顶角平分线(或底边中线或底边高线)
所在直线
第 * 页
第 * 页
三
相等
等腰
60°
第 * 页
60°
重合
3
第 * 页
90°
a2+b2=c2
第 * 页
余角
等于
等于
一半
30°
一半
第 * 页
第 * 页
1.(2019·贵州毕节中考)在下列长度的三条线段中,不能组成三角形的是 ( )
A.2 cm,3 cm,4 cm B.3 cm,6 cm,7 cm
C.2 cm,2 cm,6 cm D.5 cm,6 cm,7 cm
C
1 三角形与多边形
第 * 页
C
第 * 页
3.(2019·湖北咸宁中考)若正多边形的内角和是540°,则该正多边形的一个外角为 ( )
A.45° B.60°
C.72° D.90°
C
第 * 页
4.(广西中考)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于 ( )
A.40° B.45°
C.50° D.55°
C
第 * 页
5.(湖北黄石中考)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD= ( )
A.75°
B.80°
C.85°
D.90°
A
第 * 页
6.(2018·贵州贵阳中考)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为 ( )
A.24
B.18
C.12
D.9
A
第 * 页
7.(湖南邵阳中考)如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是________.
40°
第 * 页
8.(江苏南京中考)如图,五边形ABCDE是正五边形.若l1∥l2,则∠1-∠2=________.
72°
第 * 页
9.(湖北宜昌中考)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
第 * 页
第 * 页
D
第 * 页
12.(2019·贵州铜仁中考)如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为 ( )
A.12 B.14
C.24 D.21
A
第 * 页
13.(山东聊城中考)如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是_______________________.
14.(甘肃白银中考)已知a、b、c是△ABC的三边长,a、b满足|a-7|+(b-1)2=0,c为奇数,则c=_____.
15.(四川广安中考)若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是______.
16.(2018·贵州三州联考)三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的解,则此三角形周长是______.
540°或360°或180°
7
35
13
第 * 页
17.(贵州贵阳模拟)四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图1),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?已知:在四边形ABCD中,O是对角线BD上任意一点,如图1.求证:S△OBC·S△OAD=S△OAB·S△OCD;
(2)在三角形中(如图2),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明:若不能,说明理由.
图1
图2
第 * 页
第 * 页
第 * 页
1.(2018·贵州安顺中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的两根,则该等腰三角形的周长是 ( )
A.12 B.9
C.13 D.12或9
A
2 等腰三角形与直角三角形
第 * 页
B
第 * 页
3.(2019·湖北黄石中考)如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和∠BDC的平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD+∠CED= ( )
A.125° B.145°
C.175° D.190°
C
第 * 页
第 * 页
5.(2019·湖南邵阳中考)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是_____.
4
第 * 页
36
第 * 页
8.(广西桂林中考)如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是_____.
3
第 * 页
9.(吉林长春中考)如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为______.
10
第 * 页
10.(湖北黄冈中考)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为______cm.(杯壁厚度不计)
20
第 * 页
11.(2018·贵州贵阳中考)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积.
第 * 页
(1)证明:∵AB与AG关于AE对称,∴AE⊥BC.∵四边形ABCD是平行四边形,∴AD∥BC,∴AE⊥AD,即∠DAE=90°.∵点F是DE的中点,∴AF是Rt△ADE的中线,∴AF=EF=DF.∵AE与AF关于AG对称,∴AE=AF,∴AE=AF=EF,∴△AEF是等边三角形.
第 * 页
第 * 页
12.(2017·贵州黔南中考)如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是________.
40°
第 * 页
4
第 * 页
第 * 页
15.(黑龙江中考)如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为
S2,△B3C2B4的面积为S3,如此下去,则Sn=__________.
第 * 页
16.(浙江绍兴中考)数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题;
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
第 * 页
三角形与多边形
第 * 页
首尾顺次
第 * 页
直
锐
钝
等边
第 * 页
2.三角形中的重要线段——三角形的角平分线、中线、高、中位线和中垂线
(1)三角形的角平分线.
概念:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点和交点的线段叫做三角形的⑥____________.
性质:Ⅰ.如图,若AD为△ABC的角平分线,则有∠BAD=∠CAD;
Ⅱ.三角形角平分线上的点到角两边的距离⑦________;
Ⅲ.三角形有三条角平分线,均在三角形的⑧________;
Ⅳ.三角形的三条角平分线交于一点,该点到三角形三边的距离均相等,称为三角形的⑨________.
角平分线
相等
内部
内心
第 * 页
(2)三角形的中线.
概念:三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的⑩________.反过来,若AD为△ABC的BC边上的中线,则有BD=CD.
性质:三角形的三条中线均在三角形的?________,且相交于一点,该点称为三角形的?________.每一条中线都将三角形分成面积?________的两部分.
中线
内部
重心
相等
第 * 页
(3)三角形的高.
从三角形一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫做三角形这条边上的?______.
高
第 * 页
(2)如图,三角形都有三条高.锐角三角形的三条高都在三角形的?________;直角三角形有一条高在三角形的内部,另两条高恰好是它的?______________;钝角三角形一条高在三角形的?________,另两条高在三角形的?________.
内部
两条直角边
内部
外部
第 * 页
中点
平行
一半
第 * 页
(5)三角形的中垂线.
三角形的边的中垂线有时也叫三角形的中垂线.三角形中垂线的交点是三角形的外心,三角形的外心到三角形三个顶点的距离相等.
第 * 页
二 三角形的性质
1. 三角形的稳定性
定义:如果三角形三边的长度固定,那么三角形的形状和大小就能唯一确定下来.三角形的这个性质叫做三角形的稳定性.
应用:三角形的稳定性是三角形独有的性质,在现实生活中应用非常广泛.例如:大桥的钢架做成三角形、高压电线的支架做成三角形等.
第 * 页
大于
小于
第 * 页
180°
180°
第 * 页
等于
大于
第 * 页
360°
大角
小角
第 * 页
第 * 页
(2)凸多边形.
把一个多边形任意一边向两方无限延长成为一条直线,如果多边形的其余各边均在此直线的同旁,那么这个多边形就叫做凸多边形.例如:图1中的多边形ABCDE为凸多边形,图2中的多边形ABCDE不是凸多边形.
第 * 页
(n-2)×180°
360°
(n-3)
(n-2)
第 * 页
相等
相等
轴对称
n
中心对称
轴对称
n
第 * 页
相等
等边
第 * 页
等角
相等
重合
⊥
=
⊥
=
=
=
轴对称
顶角平分线(或底边中线或底边高线)
所在直线
第 * 页
第 * 页
三
相等
等腰
60°
第 * 页
60°
重合
3
第 * 页
90°
a2+b2=c2
第 * 页
余角
等于
等于
一半
30°
一半
第 * 页
第 * 页
1.(2019·贵州毕节中考)在下列长度的三条线段中,不能组成三角形的是 ( )
A.2 cm,3 cm,4 cm B.3 cm,6 cm,7 cm
C.2 cm,2 cm,6 cm D.5 cm,6 cm,7 cm
C
1 三角形与多边形
第 * 页
C
第 * 页
3.(2019·湖北咸宁中考)若正多边形的内角和是540°,则该正多边形的一个外角为 ( )
A.45° B.60°
C.72° D.90°
C
第 * 页
4.(广西中考)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于 ( )
A.40° B.45°
C.50° D.55°
C
第 * 页
5.(湖北黄石中考)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD= ( )
A.75°
B.80°
C.85°
D.90°
A
第 * 页
6.(2018·贵州贵阳中考)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为 ( )
A.24
B.18
C.12
D.9
A
第 * 页
7.(湖南邵阳中考)如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是________.
40°
第 * 页
8.(江苏南京中考)如图,五边形ABCDE是正五边形.若l1∥l2,则∠1-∠2=________.
72°
第 * 页
9.(湖北宜昌中考)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
第 * 页
第 * 页
D
第 * 页
12.(2019·贵州铜仁中考)如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为 ( )
A.12 B.14
C.24 D.21
A
第 * 页
13.(山东聊城中考)如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是_______________________.
14.(甘肃白银中考)已知a、b、c是△ABC的三边长,a、b满足|a-7|+(b-1)2=0,c为奇数,则c=_____.
15.(四川广安中考)若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是______.
16.(2018·贵州三州联考)三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的解,则此三角形周长是______.
540°或360°或180°
7
35
13
第 * 页
17.(贵州贵阳模拟)四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图1),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?已知:在四边形ABCD中,O是对角线BD上任意一点,如图1.求证:S△OBC·S△OAD=S△OAB·S△OCD;
(2)在三角形中(如图2),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明:若不能,说明理由.
图1
图2
第 * 页
第 * 页
第 * 页
1.(2018·贵州安顺中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的两根,则该等腰三角形的周长是 ( )
A.12 B.9
C.13 D.12或9
A
2 等腰三角形与直角三角形
第 * 页
B
第 * 页
3.(2019·湖北黄石中考)如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和∠BDC的平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD+∠CED= ( )
A.125° B.145°
C.175° D.190°
C
第 * 页
第 * 页
5.(2019·湖南邵阳中考)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是_____.
4
第 * 页
36
第 * 页
8.(广西桂林中考)如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是_____.
3
第 * 页
9.(吉林长春中考)如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为______.
10
第 * 页
10.(湖北黄冈中考)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为______cm.(杯壁厚度不计)
20
第 * 页
11.(2018·贵州贵阳中考)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积.
第 * 页
(1)证明:∵AB与AG关于AE对称,∴AE⊥BC.∵四边形ABCD是平行四边形,∴AD∥BC,∴AE⊥AD,即∠DAE=90°.∵点F是DE的中点,∴AF是Rt△ADE的中线,∴AF=EF=DF.∵AE与AF关于AG对称,∴AE=AF,∴AE=AF=EF,∴△AEF是等边三角形.
第 * 页
第 * 页
12.(2017·贵州黔南中考)如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是________.
40°
第 * 页
4
第 * 页
第 * 页
15.(黑龙江中考)如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为
S2,△B3C2B4的面积为S3,如此下去,则Sn=__________.
第 * 页
16.(浙江绍兴中考)数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题;
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
第 * 页
同课章节目录
