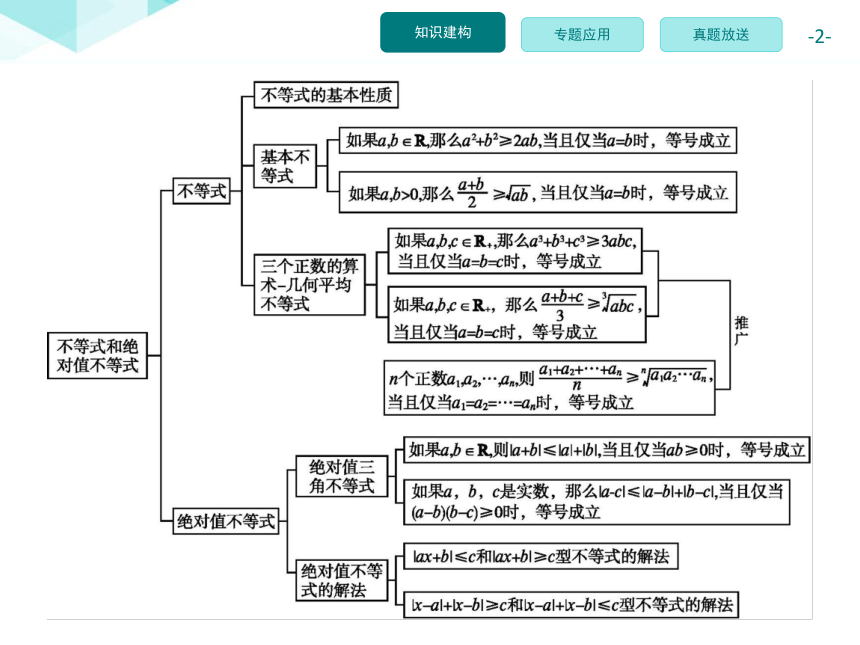
人教新课标A版 选修4-5 第一讲 不等式和绝对值不等式 整合(共24张PPT)
文档属性
| 名称 | 人教新课标A版 选修4-5 第一讲 不等式和绝对值不等式 整合(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
本讲整合
专题一
专题二
专题三
专题四
专题五
不等式性质的应用
利用不等式的性质判断不等式或有关结论是否成立,进行数值或代数式大小的比较,常用到分类讨论的思想.
【应用】 若a,b是任意实数,且a>b,则( )
提示:为提高解题速度,特殊值法与不等式性质的运用可以交替进行.
解析:a>b并不保证a,b均为正数,从而不能保证选项A,B成立.又a>b?a-b>0,但不能保证a-b>1,从而不能保证选项C成立.显然只有
答案:D
专题一
专题二
专题三
专题四
专题五
基本不等式与三个正数的算术-几何平均不等式
定理1:如果a,b∈R,那么a2+b2≥2ab,当且仅当a=b时,等号成立.
算术-几何平均不等式:
语言表述:n个正数的算术平均不小于它们的几何平均.
专题一
专题二
专题三
专题四
专题五
专题一
专题二
专题三
专题四
专题五
求证:Q(x,y)≥A(x,y)≥G(x,y)≥H(x,y).
即Q(x,y)≥A(x,y).
由基本不等式,得A(x,y)≥G(x,y).
即G(x,y)≥H(x,y).
综上所述,Q(x,y)≥A(x,y)≥G(x,y)≥H(x,y).
专题一
专题二
专题三
专题四
专题五
利用基本不等式或三个正数的算术-几何平均不等式求最大(小)值
重要的结论:
已知x,y都是正实数,则:
专题一
专题二
专题三
专题四
专题五
【应用1】 求函数y=2x2+ (x>0)的最小值.下列解法是否正确?为什么?
专题一
专题二
专题三
专题四
专题五
解:题目中两种解法均有错误.解法一错在等号不成立,
专题一
专题二
专题三
专题四
专题五
【应用2】 设计一幅宣传画,要求画面面积为4 840 cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8 cm的空白,左、右各留5 cm的空白.怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
提示:在应用平均不等式解决这类实际问题时,应注意:①设变量,一般把要求最大值和最小值的变量设为函数;②建立相应的函数关系式,把实际问题抽象为函数的最值问题;③在定义域内,求函数的最大值或最小值.
专题一
专题二
专题三
专题四
专题五
故当画面的高为88 cm,宽为55 cm时,才能使所用纸张面积最小.
专题一
专题二
专题三
专题四
专题五
含有绝对值的不等式的解法
关于含有绝对值的不等式的问题,主要包括两类:一类是解不等式,另一类是证明不等式.
1.解在绝对值符号内含有未知数的不等式(也称绝对值不等式),关键在于去掉绝对值符号,化成一般的不等式.主要的依据是绝对值的定义.
在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值,
专题一
专题二
专题三
专题四
专题五
2.含有绝对值的不等式有两种基本的类型.
第一种类型:设a为正数.根据绝对值的定义,不等式|x|
如果给定的不等式符合上述形式,就可以直接利用它的结果来解.
第二种类型:设a为正数.根据绝对值的定义,不等式|x|>a的解集是{x|x>a或x<-a}.
它的几何意义就是数轴上到原点的距离大于a的点的集合是两个开区间(-∞,-a),(a,+∞)的并集.如图所示.
同样,如果给定的不等式符合这种类型,就可以直接利用它的结果来解.
专题一
专题二
专题三
专题四
专题五
【应用1】 设有关于x的不等式lg(|x+3|+|x-7|)>a.
(1)当a=1时,解此不等式;
(2)当a为何值时,此不等式的解集是R?
解:(1)当a=1时,lg(|x+3|+|x-7|)>1,
?|x+3|+|x-7|>10
?x>7或x<-3.
所以原不等式的解集为{x|x<-3或x>7}.
(2)设f(x)=|x+3|+|x-7|,有f(x)≥|(x+3)-(x-7)|=10,
当且仅当(x+3)(x-7)≤0,即-3≤x≤7时,f(x)取得最小值10.
故lg(|x+3|+|x-7|)≥1.
要使lg(|x+3|+|x-7|)>a的解集为R,只要a<1.
专题一
专题二
专题三
专题四
专题五
【应用2】 设函数f(x)=|2x-4|+1.
(1)画出函数y=f(x)的图象;
(2)若不等式f(x)≤ax的解集非空,求a的取值范围.
专题一
专题二
专题三
专题四
专题五
则函数y=f(x)的图象如图所示.
专题一
专题二
专题三
专题四
专题五
含有绝对值的不等式的证明
证明一个含有绝对值的不等式成立,除了要应用一般不等式的基本性质之外,经常还要用到关于绝对值的和、差、积、商的性质:(1)|a|+|b|≥|a+b|;(2)|a|-|b|≤|a+b|;(3)|a|·|b|=|a·b|;
专题一
专题二
专题三
专题四
专题五
求证:|(x+y)-(a+b)|除法法则直接推出;而绝对值的差的性质可以利用和的性质导出.因此,只要能够证明|a|+|b|≥|a+b|对于任意实数都成立即可.含有绝对值的不等式的证明中,常常利用|a|≥a,|a|≥-a及绝对值的和的性质.
证明:|(x+y)-(a+b)|=|(x-a)+(y-b)|≤|x-a|+|y-b|.①
由①②,得|(x+y)-(a+b)|2
3
4
1
解析:∵a,b∈R,且ab>0,
答案:4
2
3
4
1
2.(2017·江苏,10)某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是 .?
答案:30
2
3
4
1
3.(2017·全国1,理23)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
解:(1)当a=1时,不等式f(x)≥g(x)等价于x2-x+|x+1|+|x-1|-4≤0.①
当x<-1时,①式化为x2-3x-4≤0,无解;
当-1≤x≤1时,①式化为x2-x-2≤0,从而-1≤x≤1;
2
3
4
1
(2)当x∈[-1,1]时,g(x)=2.
所以f(x)≥g(x)的解集包含[-1,1],等价于当x∈[-1,1]时f(x)≥2.
又f(x)在[-1,1]的最小值必为f(-1)与f(1)之一,
所以f(-1)≥2且f(1)≥2,
得-1≤a≤1.
所以a的取值范围为[-1,1].
2
3
4
1
4.(2017·全国3,理23)已知函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
当x<-1时,f(x)≥1无解;
当-1≤x≤2时,由f(x)≥1得,2x-1≥1,
解得1≤x≤2;
当x>2时,由f(x)≥1解得x>2.
所以f(x)≥1的解集为{x|x≥1}.
2
3
4
1
(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.
而|x+1|-|x-2|-x2+x
≤|x|+1+|x|-2-x2+|x|
本讲整合
专题一
专题二
专题三
专题四
专题五
不等式性质的应用
利用不等式的性质判断不等式或有关结论是否成立,进行数值或代数式大小的比较,常用到分类讨论的思想.
【应用】 若a,b是任意实数,且a>b,则( )
提示:为提高解题速度,特殊值法与不等式性质的运用可以交替进行.
解析:a>b并不保证a,b均为正数,从而不能保证选项A,B成立.又a>b?a-b>0,但不能保证a-b>1,从而不能保证选项C成立.显然只有
答案:D
专题一
专题二
专题三
专题四
专题五
基本不等式与三个正数的算术-几何平均不等式
定理1:如果a,b∈R,那么a2+b2≥2ab,当且仅当a=b时,等号成立.
算术-几何平均不等式:
语言表述:n个正数的算术平均不小于它们的几何平均.
专题一
专题二
专题三
专题四
专题五
专题一
专题二
专题三
专题四
专题五
求证:Q(x,y)≥A(x,y)≥G(x,y)≥H(x,y).
即Q(x,y)≥A(x,y).
由基本不等式,得A(x,y)≥G(x,y).
即G(x,y)≥H(x,y).
综上所述,Q(x,y)≥A(x,y)≥G(x,y)≥H(x,y).
专题一
专题二
专题三
专题四
专题五
利用基本不等式或三个正数的算术-几何平均不等式求最大(小)值
重要的结论:
已知x,y都是正实数,则:
专题一
专题二
专题三
专题四
专题五
【应用1】 求函数y=2x2+ (x>0)的最小值.下列解法是否正确?为什么?
专题一
专题二
专题三
专题四
专题五
解:题目中两种解法均有错误.解法一错在等号不成立,
专题一
专题二
专题三
专题四
专题五
【应用2】 设计一幅宣传画,要求画面面积为4 840 cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8 cm的空白,左、右各留5 cm的空白.怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
提示:在应用平均不等式解决这类实际问题时,应注意:①设变量,一般把要求最大值和最小值的变量设为函数;②建立相应的函数关系式,把实际问题抽象为函数的最值问题;③在定义域内,求函数的最大值或最小值.
专题一
专题二
专题三
专题四
专题五
故当画面的高为88 cm,宽为55 cm时,才能使所用纸张面积最小.
专题一
专题二
专题三
专题四
专题五
含有绝对值的不等式的解法
关于含有绝对值的不等式的问题,主要包括两类:一类是解不等式,另一类是证明不等式.
1.解在绝对值符号内含有未知数的不等式(也称绝对值不等式),关键在于去掉绝对值符号,化成一般的不等式.主要的依据是绝对值的定义.
在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值,
专题一
专题二
专题三
专题四
专题五
2.含有绝对值的不等式有两种基本的类型.
第一种类型:设a为正数.根据绝对值的定义,不等式|x|
如果给定的不等式符合上述形式,就可以直接利用它的结果来解.
第二种类型:设a为正数.根据绝对值的定义,不等式|x|>a的解集是{x|x>a或x<-a}.
它的几何意义就是数轴上到原点的距离大于a的点的集合是两个开区间(-∞,-a),(a,+∞)的并集.如图所示.
同样,如果给定的不等式符合这种类型,就可以直接利用它的结果来解.
专题一
专题二
专题三
专题四
专题五
【应用1】 设有关于x的不等式lg(|x+3|+|x-7|)>a.
(1)当a=1时,解此不等式;
(2)当a为何值时,此不等式的解集是R?
解:(1)当a=1时,lg(|x+3|+|x-7|)>1,
?|x+3|+|x-7|>10
?x>7或x<-3.
所以原不等式的解集为{x|x<-3或x>7}.
(2)设f(x)=|x+3|+|x-7|,有f(x)≥|(x+3)-(x-7)|=10,
当且仅当(x+3)(x-7)≤0,即-3≤x≤7时,f(x)取得最小值10.
故lg(|x+3|+|x-7|)≥1.
要使lg(|x+3|+|x-7|)>a的解集为R,只要a<1.
专题一
专题二
专题三
专题四
专题五
【应用2】 设函数f(x)=|2x-4|+1.
(1)画出函数y=f(x)的图象;
(2)若不等式f(x)≤ax的解集非空,求a的取值范围.
专题一
专题二
专题三
专题四
专题五
则函数y=f(x)的图象如图所示.
专题一
专题二
专题三
专题四
专题五
含有绝对值的不等式的证明
证明一个含有绝对值的不等式成立,除了要应用一般不等式的基本性质之外,经常还要用到关于绝对值的和、差、积、商的性质:(1)|a|+|b|≥|a+b|;(2)|a|-|b|≤|a+b|;(3)|a|·|b|=|a·b|;
专题一
专题二
专题三
专题四
专题五
求证:|(x+y)-(a+b)|
证明:|(x+y)-(a+b)|=|(x-a)+(y-b)|≤|x-a|+|y-b|.①
由①②,得|(x+y)-(a+b)|
3
4
1
解析:∵a,b∈R,且ab>0,
答案:4
2
3
4
1
2.(2017·江苏,10)某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是 .?
答案:30
2
3
4
1
3.(2017·全国1,理23)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
解:(1)当a=1时,不等式f(x)≥g(x)等价于x2-x+|x+1|+|x-1|-4≤0.①
当x<-1时,①式化为x2-3x-4≤0,无解;
当-1≤x≤1时,①式化为x2-x-2≤0,从而-1≤x≤1;
2
3
4
1
(2)当x∈[-1,1]时,g(x)=2.
所以f(x)≥g(x)的解集包含[-1,1],等价于当x∈[-1,1]时f(x)≥2.
又f(x)在[-1,1]的最小值必为f(-1)与f(1)之一,
所以f(-1)≥2且f(1)≥2,
得-1≤a≤1.
所以a的取值范围为[-1,1].
2
3
4
1
4.(2017·全国3,理23)已知函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
当x<-1时,f(x)≥1无解;
当-1≤x≤2时,由f(x)≥1得,2x-1≥1,
解得1≤x≤2;
当x>2时,由f(x)≥1解得x>2.
所以f(x)≥1的解集为{x|x≥1}.
2
3
4
1
(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.
而|x+1|-|x-2|-x2+x
≤|x|+1+|x|-2-x2+|x|
