沪科版七年级下册数学:8.1.1同底数幂的乘法课件(25张PPT)
文档属性
| 名称 | 沪科版七年级下册数学:8.1.1同底数幂的乘法课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 20:28:26 | ||
图片预览








文档简介
(共25张PPT)
第8章整式乘法与因式分解
义务教育教科书 数学 七年级下册
8.1 幂的运算
1 . 同底数幂的乘法
教学目标:
1、了解同底数幂的意义与运算性质,并能运用同底数幂的运算性质进行计算。
2、经历探索同底数幂的运算性质的过程,发展学生观察、概括与抽象的能力。
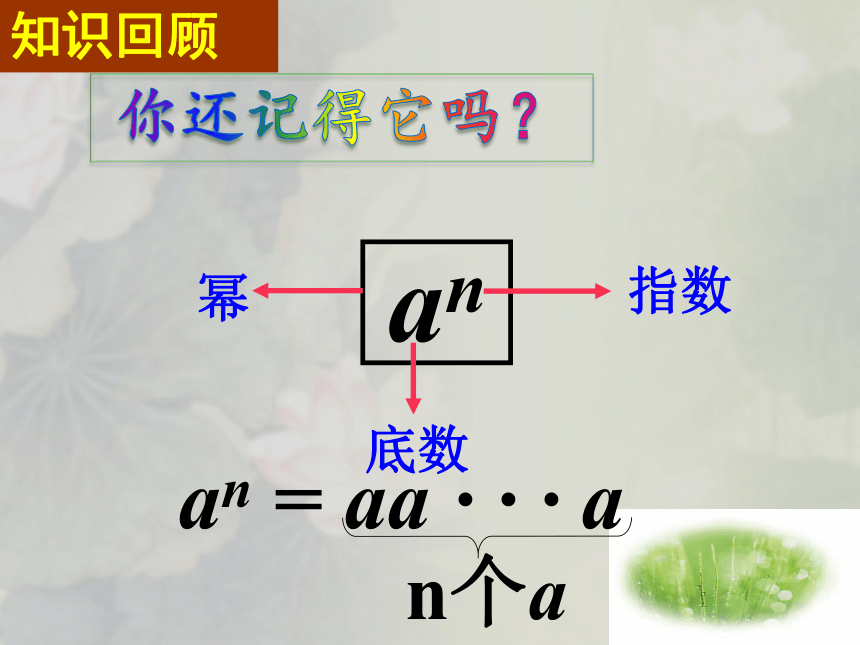
an
an = aa · · · a
n个a
知识回顾
你能根据an的乘法意义, 将下列各式写成乘法形式吗?
(1) -24
(2) (-2)4
=-2×2×2×2
=(-2)×(-2)×(-2)×(-2)
知识回顾
怎样计算1015× 103 呢?
小资料:
????“天河一号”由国防科学技术大学研制,部署在国家超级计算天津中心,其实测运算速度可以达到每秒2570万亿次。
提出问题
=27
(1) 25 ×22
(2) a3 · a2
=(2 ×2 ×2 ×2 ×2 ) ×(2 ×2)
= 2 ×2 ×2 ×2 × 2 ×2 ×2
=(a · a · a) (a · a)
=a5
想一想
你能根据乘方的意义算出下列式子
的结果吗?
(2) a3 · a2
(1) 25 ×22
(3)5m · 5n
(3)5m · 5n
=5m+n
=(5 × 5 × · · · × 5) ×(5 × 5 × · · · × 5)
=5 × 5 × · · · · · · × 5 × 5
想一想
你能根据乘方的意义算出下列式子
的结果吗?
(2) a3 · a2
(1) 25 ×22
(3)5m · 5n
=27
这几道题有什么共同的特点呢?
(1)25 ×22
=a5
(3)5m · 5n
=5m+n
(2)a3 · a2
=(a · a · a) (a · a)
=(2 ×2 ×2 ×2 ×2 ) ×(2 ×2)
=(5 × 5 × · · · × 5) ×(5 × 5 × · · · × 5)
=25+2
=a3+2
想一想
am · an =
m个a
n个a
= aa · · · a
=am+n
(m+n)个a
(aa · · · a)
(aa · · · a)
猜一猜
当m,n为正整数时, am·an =?
一般地,如果m,n都是正整数,那么
am · an = am+n
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
运算形式
运算方法
(同底、乘法)
(底不变、指相加)
知识推导
想一想: ?当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
知识推导
am·an·…·ap =
am+n+…+p
(m、n、…、p都是正整数)
(1)25 ×22
=a7
=27
(2)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2 ×2 ×2 ) ×(2 ×2)
=25+2
=a3+4
知识应用
解:
(3)5m · 5n
=5m+n
x2.x5 (2) a · a6
(3)(-2)×(-2)4×(-2)3 (4) xm · x3m+1
知识应用
算一算:
8.1.1同底数幂的乘法
am · an = am+n
am · an = am+n
知识应用
辩一辩
判断下列计算是否正确,并简要说明理由:
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
c · c3 = c4
×
×
√
×
×
×
c=c1
填一填:
am · an = am+n
知识应用
(1)b5 ·b=( ) (2)10 ·102 ·103 =( )
(3)-a2 · a6= ( ) (4)y2n ·yn+1=( )
b6
106
-a8
y3n+1
练一练:
(1)
(2)
(3)
(4)
知识拓展
am · an = am+n
8.1.1同底数幂的乘法
1.已知:am=2, an=3.
求am+n =?
解: am+n = am · an
=2 × 3
=6
议一议
知识拓展
自我评价
第1-4项的内容只要在等级栏里打“√”
内容 自我评价
优秀 良好 加油
1、能理解同底数幂的乘法运算性质
2、会用性质进行同底数幂的乘法运算
3、能把自己的想法与他人分享
4、能认真倾听他人的想法、见解
5、本节课你还有哪些疑惑的问题
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
课堂小结
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子 公式 应用
不变,
相加。
am · an · ap = am+n+p (m、n、p正整数)
1、下列各式的结果等于26的是( )
A 2+25 B 2 x25
C 23x25 D 0.22x0.24
2、下列计算结果正确的是( )
A a3 · a3=a9 B m2 · n2=mn4
C xm · x3=x3m D y · yn=yn+1
B
D
效果检测
8.1.1同底数幂的乘法
am · an = am+n
则正整数x , y的值有( )
(A)1对 (B)2对 (C)3对 (D)4对
3.
4.
5.
2
D
效果检测
课后作业
1.必做题:计算下列各题:
(1) (2)
(3) (4)
2.选做题:已知x3·xa·x2a+1=x31,求a的值.
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.祝大家学有所得!
结束寄语
下课了
第8章整式乘法与因式分解
义务教育教科书 数学 七年级下册
8.1 幂的运算
1 . 同底数幂的乘法
教学目标:
1、了解同底数幂的意义与运算性质,并能运用同底数幂的运算性质进行计算。
2、经历探索同底数幂的运算性质的过程,发展学生观察、概括与抽象的能力。
an
an = aa · · · a
n个a
知识回顾
你能根据an的乘法意义, 将下列各式写成乘法形式吗?
(1) -24
(2) (-2)4
=-2×2×2×2
=(-2)×(-2)×(-2)×(-2)
知识回顾
怎样计算1015× 103 呢?
小资料:
????“天河一号”由国防科学技术大学研制,部署在国家超级计算天津中心,其实测运算速度可以达到每秒2570万亿次。
提出问题
=27
(1) 25 ×22
(2) a3 · a2
=(2 ×2 ×2 ×2 ×2 ) ×(2 ×2)
= 2 ×2 ×2 ×2 × 2 ×2 ×2
=(a · a · a) (a · a)
=a5
想一想
你能根据乘方的意义算出下列式子
的结果吗?
(2) a3 · a2
(1) 25 ×22
(3)5m · 5n
(3)5m · 5n
=5m+n
=(5 × 5 × · · · × 5) ×(5 × 5 × · · · × 5)
=5 × 5 × · · · · · · × 5 × 5
想一想
你能根据乘方的意义算出下列式子
的结果吗?
(2) a3 · a2
(1) 25 ×22
(3)5m · 5n
=27
这几道题有什么共同的特点呢?
(1)25 ×22
=a5
(3)5m · 5n
=5m+n
(2)a3 · a2
=(a · a · a) (a · a)
=(2 ×2 ×2 ×2 ×2 ) ×(2 ×2)
=(5 × 5 × · · · × 5) ×(5 × 5 × · · · × 5)
=25+2
=a3+2
想一想
am · an =
m个a
n个a
= aa · · · a
=am+n
(m+n)个a
(aa · · · a)
(aa · · · a)
猜一猜
当m,n为正整数时, am·an =?
一般地,如果m,n都是正整数,那么
am · an = am+n
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
运算形式
运算方法
(同底、乘法)
(底不变、指相加)
知识推导
想一想: ?当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
知识推导
am·an·…·ap =
am+n+…+p
(m、n、…、p都是正整数)
(1)25 ×22
=a7
=27
(2)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2 ×2 ×2 ) ×(2 ×2)
=25+2
=a3+4
知识应用
解:
(3)5m · 5n
=5m+n
x2.x5 (2) a · a6
(3)(-2)×(-2)4×(-2)3 (4) xm · x3m+1
知识应用
算一算:
8.1.1同底数幂的乘法
am · an = am+n
am · an = am+n
知识应用
辩一辩
判断下列计算是否正确,并简要说明理由:
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
c · c3 = c4
×
×
√
×
×
×
c=c1
填一填:
am · an = am+n
知识应用
(1)b5 ·b=( ) (2)10 ·102 ·103 =( )
(3)-a2 · a6= ( ) (4)y2n ·yn+1=( )
b6
106
-a8
y3n+1
练一练:
(1)
(2)
(3)
(4)
知识拓展
am · an = am+n
8.1.1同底数幂的乘法
1.已知:am=2, an=3.
求am+n =?
解: am+n = am · an
=2 × 3
=6
议一议
知识拓展
自我评价
第1-4项的内容只要在等级栏里打“√”
内容 自我评价
优秀 良好 加油
1、能理解同底数幂的乘法运算性质
2、会用性质进行同底数幂的乘法运算
3、能把自己的想法与他人分享
4、能认真倾听他人的想法、见解
5、本节课你还有哪些疑惑的问题
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
课堂小结
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子 公式 应用
不变,
相加。
am · an · ap = am+n+p (m、n、p正整数)
1、下列各式的结果等于26的是( )
A 2+25 B 2 x25
C 23x25 D 0.22x0.24
2、下列计算结果正确的是( )
A a3 · a3=a9 B m2 · n2=mn4
C xm · x3=x3m D y · yn=yn+1
B
D
效果检测
8.1.1同底数幂的乘法
am · an = am+n
则正整数x , y的值有( )
(A)1对 (B)2对 (C)3对 (D)4对
3.
4.
5.
2
D
效果检测
课后作业
1.必做题:计算下列各题:
(1) (2)
(3) (4)
2.选做题:已知x3·xa·x2a+1=x31,求a的值.
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.祝大家学有所得!
结束寄语
下课了
