沪科版七年级下册数学8.2整式乘法-单项式与单项式相乘课件 (22张PPT)
文档属性
| 名称 | 沪科版七年级下册数学8.2整式乘法-单项式与单项式相乘课件 (22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 541.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 19:46:48 | ||
图片预览



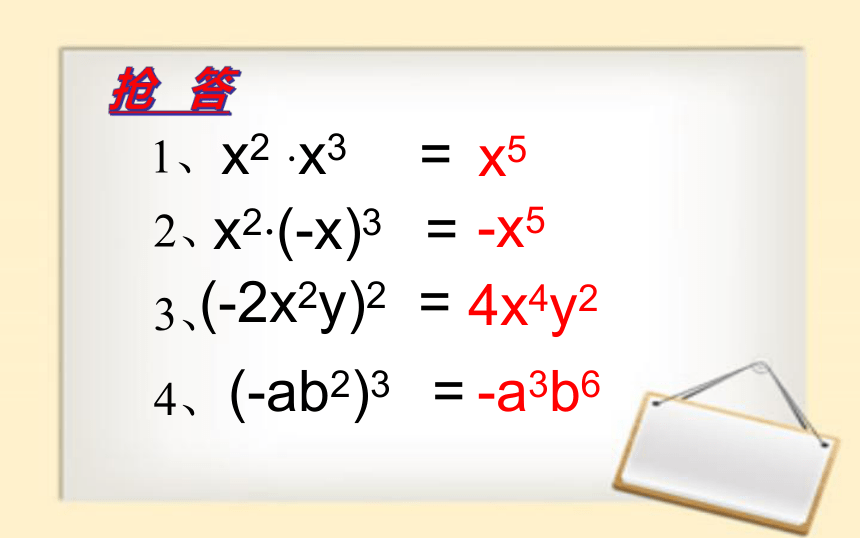





文档简介
(共22张PPT)
数字与字母的积的形式叫_______,单
独的一个数或者一个字母也叫做_____。其
中,单项式的数字因数叫做___________。
单项式
单项式
单项式的系数
幂的运算性质
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
(其中,m、n均为正整数)
x2 ·x3 =
2、
3、
4、
x5
-x5
-a3b6
1、
x2·(-x)3 =
(-ab2)3 =
4x4y2
(-2x2y)2 =
5、(a+b)2·(a+b)3=
6、[2(x-y)]3=
-3
4
7、单项式 -3x2y3 的系数是____
8、单项式 (-2xy2)2 的系数是___
(a+b)5
8(x-y)3
光的速度大约是3×105km/s,从太阳系
以外距离地球最近的一颗恒星(比邻星)
发出的光,需要4年才能到达地球,1年以
3×107s计算,试问地球与这颗恒星的距离
约为多少千米?你能列出算式吗?
(3×105)×(4×3×107)
(3×105)×(4×3×107)
=(3×4×3)×(105×107)
= 36×1012
= 3.6×1013
(乘法交换律、结合律)
想一想:如果把上面算式中的数字换成字母,该如何计算呢?
(整式乘法、同底数幂的乘法)
完成下面计算 :(小组讨论汇报结果)
4x2y·3xy2=(4×3)·(x2·___)·(y·___)
=_________
5abc·(-3ab)
=[5×(-3)]·(a·___)·(b·___)·c
=__________
x
y2
12x3y3
a
b
-15a2b2c
想一想:通过以上两题,你能归纳出单项式与单项式相乘的法则吗?(同桌位之间讨论、交流)
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式.
单项式的乘法法则:
(1)系数相乘
(2)同底数幂相乘
(3)只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.
注意符号
单项式相乘的一般步骤:
试一试
(1) (-4abc)(2ab) (2) (4×103)×(6×104)
解 (1) (-4abc)(2ab)
(2) (4×103)×(6×104)
(3) (2x)3·(-3xy2) (4) (-5a2b)(2ab2c)(-a2c)
= -8a2b2c
=(-4×2)·(a·a)·(b·b)·c
=(4×6)×(103×104)
=24×107
=2.4×108
c
试一试
=(8x3)·(-3xy2)
=[(-5)×2×(-1)](a2·a·a2)(b·b2)(c·c)
(3) (2x)3·(-3xy2)
(4) (-5a2b)(2ab2c)(-a2c)
=[8×(-3)]·(x3·x)·y2
=-24x4y2
=10a5b3c2
1. (2xy2)·(5xy)
2. (-2a2b3)·(-3a)
4. (4×105)·(5×104)·(-3×102)
3. (x2y)3·(-4xy2)
练一练
1. (2xy2)·(5xy)=
(2×5)·(x·x)·(y2·y)
= 10 x2y3
2. (-2a2b3)·(-3a)=
[(-2)×(-3)]·(a2·a)·b3
=6a3b3
4. (4×105)·(5×104)·(-3×102)
=[4×5×(-3)]·(105×104×102)
=-60×1011
=-6×1012
3. (x2y)3·(-4xy2)=
(x6y3)·(-4xy2)
=-4x7y5
下面的计算对不对?若不对,请改正。
( )
( )
( )
( )
×
×
(2) 4m5·3m= 12m5
×
(3) -(3x3)2= 9x6
×
(4)-4x2y3·5xy2z= -20x3y5
(1) 4b2·4b2 = 8b4
16
6
z
比一比,看谁做的又快又准!
拓 展
1、计算 2x2·(-x)2-x·(-x)3+(-3x2)·x2
解:原式=
2x2·x2-x·(-x3)+(-3x2)·x2
=2x4+x4-3x4
=(2+1-3)x4
=0
拓 展
2、已知3xn-3y5-n与-8x3my2n的积是2x6y2的
同类项,求m,n的值。
解:
3xn-3y5-n · (-8x3my2n)=-24x3m+n-3yn+5
由题意可知,
-24x3m+n-3yn+5与2x6y2是同类项,
所以,
解得,
拓 展
=2x8y4
=2×(-1)4=2×1=2
回顾交流:
本节课我们学习了哪些内容?
单项式与单项式相乘法则?
单项式乘以单项式,结果仍然是什么?
布置作业
1、课本65页,习题8.2, 第1、2两题
2、思考:如何计算 5x2·(2x+4)
数字与字母的积的形式叫_______,单
独的一个数或者一个字母也叫做_____。其
中,单项式的数字因数叫做___________。
单项式
单项式
单项式的系数
幂的运算性质
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
(其中,m、n均为正整数)
x2 ·x3 =
2、
3、
4、
x5
-x5
-a3b6
1、
x2·(-x)3 =
(-ab2)3 =
4x4y2
(-2x2y)2 =
5、(a+b)2·(a+b)3=
6、[2(x-y)]3=
-3
4
7、单项式 -3x2y3 的系数是____
8、单项式 (-2xy2)2 的系数是___
(a+b)5
8(x-y)3
光的速度大约是3×105km/s,从太阳系
以外距离地球最近的一颗恒星(比邻星)
发出的光,需要4年才能到达地球,1年以
3×107s计算,试问地球与这颗恒星的距离
约为多少千米?你能列出算式吗?
(3×105)×(4×3×107)
(3×105)×(4×3×107)
=(3×4×3)×(105×107)
= 36×1012
= 3.6×1013
(乘法交换律、结合律)
想一想:如果把上面算式中的数字换成字母,该如何计算呢?
(整式乘法、同底数幂的乘法)
完成下面计算 :(小组讨论汇报结果)
4x2y·3xy2=(4×3)·(x2·___)·(y·___)
=_________
5abc·(-3ab)
=[5×(-3)]·(a·___)·(b·___)·c
=__________
x
y2
12x3y3
a
b
-15a2b2c
想一想:通过以上两题,你能归纳出单项式与单项式相乘的法则吗?(同桌位之间讨论、交流)
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式.
单项式的乘法法则:
(1)系数相乘
(2)同底数幂相乘
(3)只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.
注意符号
单项式相乘的一般步骤:
试一试
(1) (-4abc)(2ab) (2) (4×103)×(6×104)
解 (1) (-4abc)(2ab)
(2) (4×103)×(6×104)
(3) (2x)3·(-3xy2) (4) (-5a2b)(2ab2c)(-a2c)
= -8a2b2c
=(-4×2)·(a·a)·(b·b)·c
=(4×6)×(103×104)
=24×107
=2.4×108
c
试一试
=(8x3)·(-3xy2)
=[(-5)×2×(-1)](a2·a·a2)(b·b2)(c·c)
(3) (2x)3·(-3xy2)
(4) (-5a2b)(2ab2c)(-a2c)
=[8×(-3)]·(x3·x)·y2
=-24x4y2
=10a5b3c2
1. (2xy2)·(5xy)
2. (-2a2b3)·(-3a)
4. (4×105)·(5×104)·(-3×102)
3. (x2y)3·(-4xy2)
练一练
1. (2xy2)·(5xy)=
(2×5)·(x·x)·(y2·y)
= 10 x2y3
2. (-2a2b3)·(-3a)=
[(-2)×(-3)]·(a2·a)·b3
=6a3b3
4. (4×105)·(5×104)·(-3×102)
=[4×5×(-3)]·(105×104×102)
=-60×1011
=-6×1012
3. (x2y)3·(-4xy2)=
(x6y3)·(-4xy2)
=-4x7y5
下面的计算对不对?若不对,请改正。
( )
( )
( )
( )
×
×
(2) 4m5·3m= 12m5
×
(3) -(3x3)2= 9x6
×
(4)-4x2y3·5xy2z= -20x3y5
(1) 4b2·4b2 = 8b4
16
6
z
比一比,看谁做的又快又准!
拓 展
1、计算 2x2·(-x)2-x·(-x)3+(-3x2)·x2
解:原式=
2x2·x2-x·(-x3)+(-3x2)·x2
=2x4+x4-3x4
=(2+1-3)x4
=0
拓 展
2、已知3xn-3y5-n与-8x3my2n的积是2x6y2的
同类项,求m,n的值。
解:
3xn-3y5-n · (-8x3my2n)=-24x3m+n-3yn+5
由题意可知,
-24x3m+n-3yn+5与2x6y2是同类项,
所以,
解得,
拓 展
=2x8y4
=2×(-1)4=2×1=2
回顾交流:
本节课我们学习了哪些内容?
单项式与单项式相乘法则?
单项式乘以单项式,结果仍然是什么?
布置作业
1、课本65页,习题8.2, 第1、2两题
2、思考:如何计算 5x2·(2x+4)
