沪科版九年级下册数学:24.5 三角形的内切圆课件(共27张PPT)
文档属性
| 名称 | 沪科版九年级下册数学:24.5 三角形的内切圆课件(共27张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
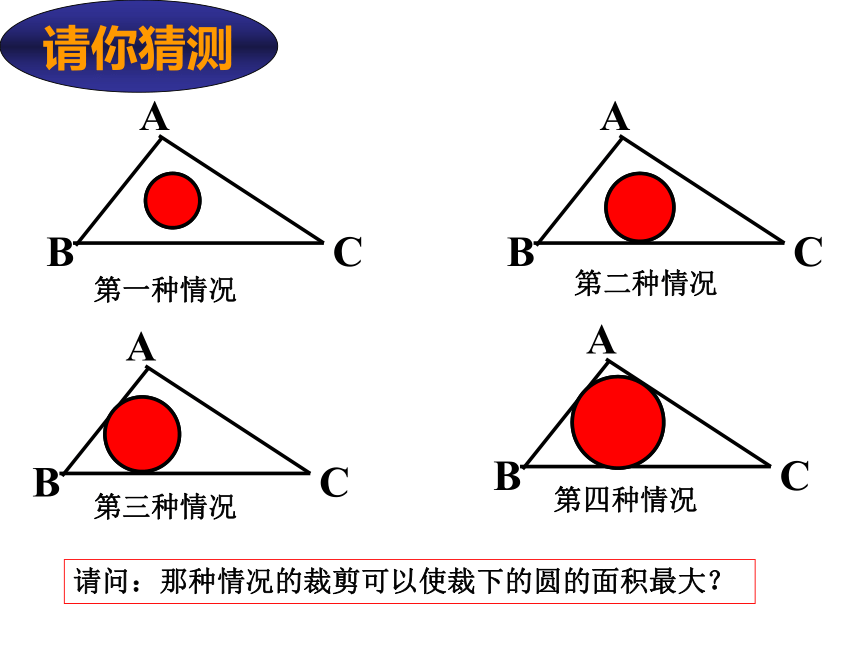
1、确定一个圆的位置与大小的条件是什么?
①.圆心与半径
2、叙述角平分线的性质与判定
性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。
3、下图中△ABC与圆O的关系?
△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心
或②.不在同一直线上的三点
A
B
C
O
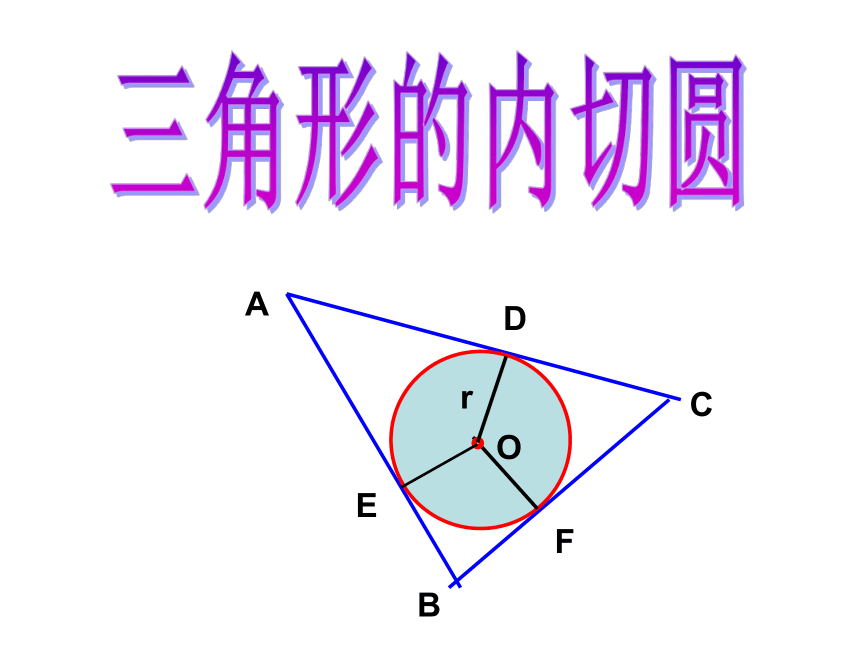
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
三角形的外接圆在实际中很有用,但还有用它不能解决的问题.如
第一种情况
第二种情况
第三种情况
第四种情况
请问:那种情况的裁剪可以使裁下的圆的面积最大?
O
r
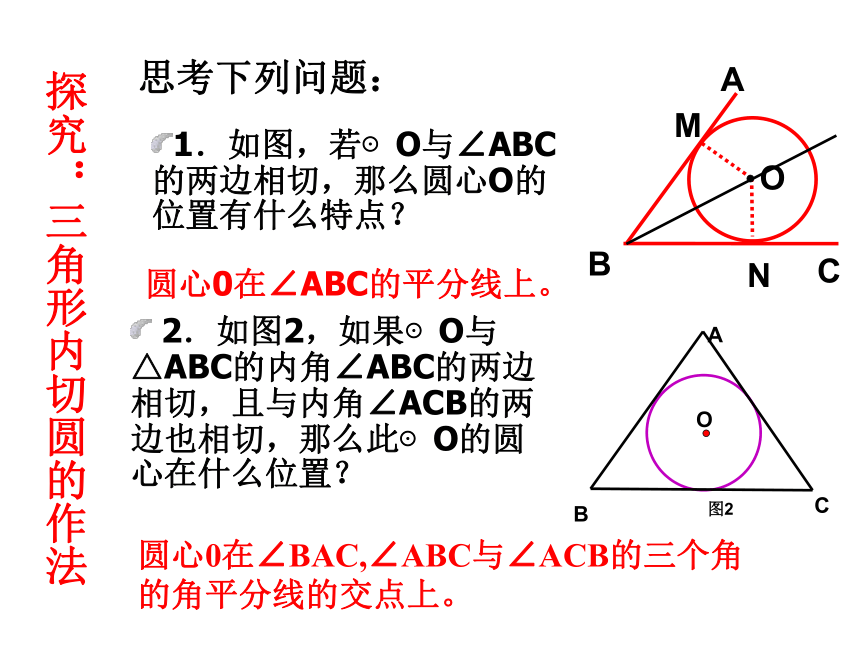
思考下列问题:
1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?
圆心0在∠ABC的平分线上。
?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?
圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。
O
M
A
B
C
N
探究:三角形内切圆的作法
作法:
A
B
C
1、作∠B、∠C的平分线
BM和CN,交点为I。
I
2.过点I作ID⊥BC,垂足为D。
3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。
M
N
试一试:
你能画出一个三角形的内切圆吗?
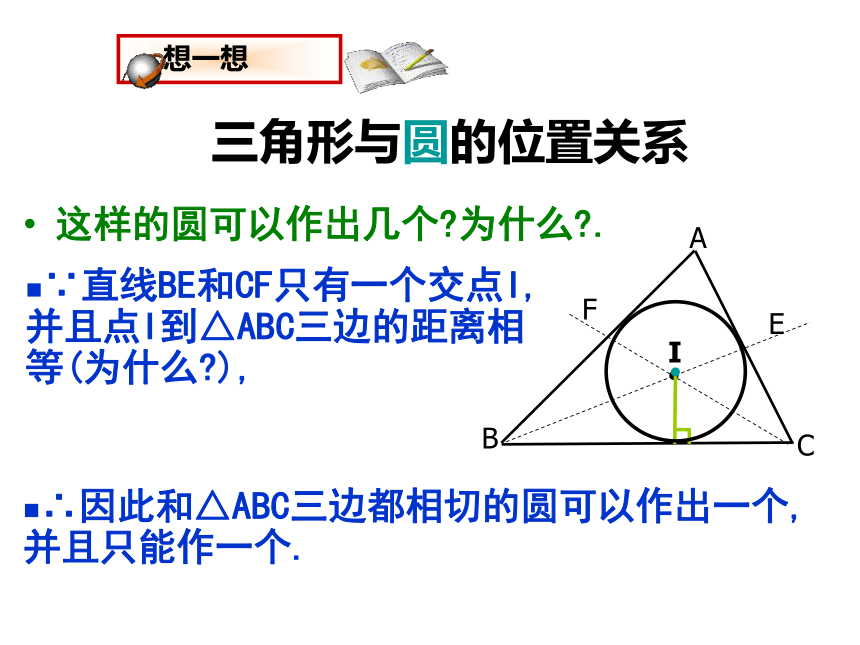
这样的圆可以作出几个?为什么?.
∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),
∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
三角形与圆的位置关系
三角形与圆的位置关系
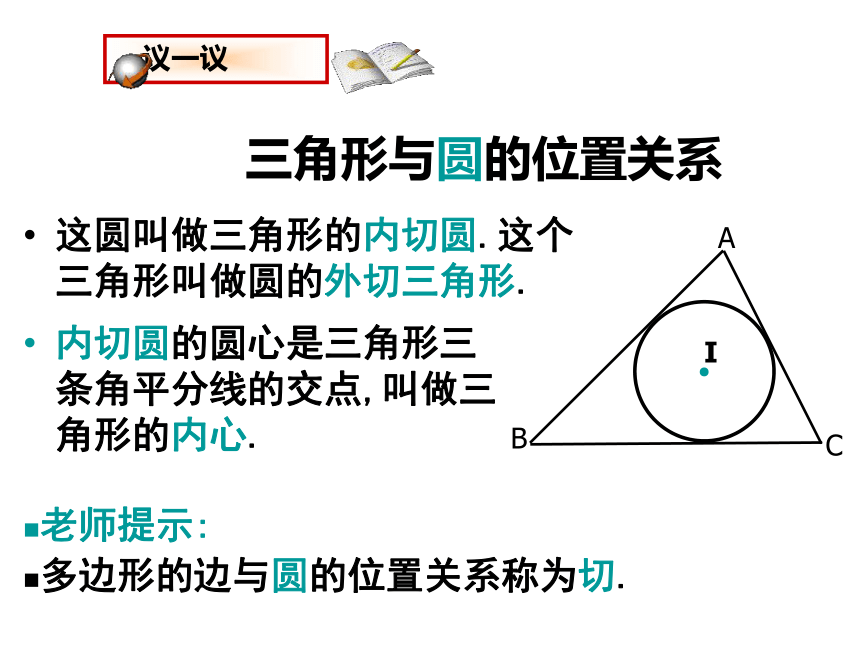
这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
老师提示:
多边形的边与圆的位置关系称为切.
定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
1.三角形的内心到三角形各边的距离相等;
性质:
O
r
2.三角形的内心在三角形的角平分线上;
内 心(三角形内切圆的圆心)
三角形三边中垂线的交点
三角形三条
角平分线的
交点
(1)OA=OB=OC
(2)外心不一定在三角形的内部.
(1)到三边的距离相等;
(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
外 心
(三角形
外接圆的
圆心)
1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。
外接
内接
外心
三边中垂线
2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。
外切
内切
内
三条角平分线
3. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在三角形的_______.
1
无数
内部
练一练
探讨1:
(1)任意一个三角形一定有一个外接圆,并且只有一个外接圆.
(2)任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
(3)任意一个三角形一定有一个内切圆,并且只有一个内切圆.
(4)任意一个圆一定有一个外切三角形,并且只有一个外切三角形
正确说法有_______________________
(1)
(3)
1.一个三角形有且只有一个内切圆;
2.一个圆有无数个外切三角形;
3.三角形的内心就是三角形三条内角平
分线的交点;
4. 三角形的内心到三角形三边的距离相等。
如图,在△ABC中,∠A=68°,点I是内心,求∠BIC的度数
老师提示:若点I是外心呢?
(2)若∠A=80 °,则∠BOC = 度。
(3)若∠BOC=100 °,则∠A = 度。
解:
130
20
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(25°+ 35 °)
=120 °
理由: ∵点O是△ABC的内心,
(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。
在△OBC中,
∠BOC =180 °-( ∠1+ ∠3 )
·
B
D
E
F
O
C
A
如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
解:设△ABC的内切圆与三边相切于D、E、F,
连结OA、OB、OC、OD、OE、OF,
则OD⊥AB,OE⊥BC,OF⊥AC.
∴S△ABC=S△AOB+S△BOC +S△AOC
设△ABC的三边为a、b、c,面积为S,
则△ABC的内切圆的半径 r=
三角形的内切圆的有关计算
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙O为Rt△ABC的内切圆. (1)求Rt△ABC的内切圆的半径 . (2)若移动点O的位置,使⊙O保持与△ABC的边AC、BC都相切,求⊙O的半径r的取值范围。
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:(1)设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
解得
r=1
在Rt△ABC中,BC=3,AC=4, ∴AB=5
由已知可得四边形ODCE为正方形,∴CD=CE=OD
∴ Rt△ABC的内切圆的半径为1。
(2)如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连结OB、OD,则四边形BODC为正方形。
·
A
B
O
D
C
∴OB=BC=3
∴半径r的取值范围为0<r≤3
几何问题代数化是解决几何问题的一种重要方法。
.
A
B
C
直角三角形的两直角边分别是5cm,12cm .则其内切圆的半径为______。
O
2cm
在△ABC中,∠C=90°,BC=3,AC=4.求这个三角形的外接圆半径和内切圆半径.
B
解:如图:由勾股定理可得:
O
∴外接圆半径R=2.5
由我们推导的三角形的面积公式可知:
解得:r=1
r
小结: 三角形的内切圆
(1)三角形的内心是三角形内切圆的圆心
(2)三角形的内心是三角形各角平分线的交点
(3)三角形内心到三边的距离相等
(4)三角形面积
(C为三角形周长,r为内切圆半径)
(5)直角三角形 的内切圆的半径为r 与 各边长 a、b、c的关系是
或
2、菱形ABCD中,周长为40,∠ABC=120°,则内切圆的半径为( )
3、如图,⊙O是△ABC的内切圆,
D、E、F是切点,∠A=50°,∠C=60°,
则∠DOE=( )
(A)70° (B)110°
(C)120° (D)130°
(A)梯形 (B)菱形 (C)矩形 (D)平行四边形
1、下列图形中,一定有内切圆的四边形是( )
B
B
D
4、等边三角形的内切圆半径、外接圆的半径和高的比为( )
5、存在内切圆和外接圆的四边形一定是( )
(A)矩形 (B)菱形
(C)正方形 (D)平行四边形
D
C
6.已知:△ABC的内切圆分别和BC、AC、AB相切于点D、E、F,∠DIE=120°,∠EIF=130°.求△ABC的三个内角的度数.
7.如图,△ABC中,E是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DE=DB
1
2
3
4
5
DB ? = AD · DF .
F
1、确定一个圆的位置与大小的条件是什么?
①.圆心与半径
2、叙述角平分线的性质与判定
性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。
3、下图中△ABC与圆O的关系?
△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心
或②.不在同一直线上的三点
A
B
C
O
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
三角形的外接圆在实际中很有用,但还有用它不能解决的问题.如
第一种情况
第二种情况
第三种情况
第四种情况
请问:那种情况的裁剪可以使裁下的圆的面积最大?
O
r
思考下列问题:
1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?
圆心0在∠ABC的平分线上。
?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?
圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。
O
M
A
B
C
N
探究:三角形内切圆的作法
作法:
A
B
C
1、作∠B、∠C的平分线
BM和CN,交点为I。
I
2.过点I作ID⊥BC,垂足为D。
3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。
M
N
试一试:
你能画出一个三角形的内切圆吗?
这样的圆可以作出几个?为什么?.
∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),
∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
三角形与圆的位置关系
三角形与圆的位置关系
这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
老师提示:
多边形的边与圆的位置关系称为切.
定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
1.三角形的内心到三角形各边的距离相等;
性质:
O
r
2.三角形的内心在三角形的角平分线上;
内 心(三角形内切圆的圆心)
三角形三边中垂线的交点
三角形三条
角平分线的
交点
(1)OA=OB=OC
(2)外心不一定在三角形的内部.
(1)到三边的距离相等;
(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
(3)内心在三角形内部.
外 心
(三角形
外接圆的
圆心)
1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。
外接
内接
外心
三边中垂线
2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。
外切
内切
内
三条角平分线
3. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在三角形的_______.
1
无数
内部
练一练
探讨1:
(1)任意一个三角形一定有一个外接圆,并且只有一个外接圆.
(2)任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
(3)任意一个三角形一定有一个内切圆,并且只有一个内切圆.
(4)任意一个圆一定有一个外切三角形,并且只有一个外切三角形
正确说法有_______________________
(1)
(3)
1.一个三角形有且只有一个内切圆;
2.一个圆有无数个外切三角形;
3.三角形的内心就是三角形三条内角平
分线的交点;
4. 三角形的内心到三角形三边的距离相等。
如图,在△ABC中,∠A=68°,点I是内心,求∠BIC的度数
老师提示:若点I是外心呢?
(2)若∠A=80 °,则∠BOC = 度。
(3)若∠BOC=100 °,则∠A = 度。
解:
130
20
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(25°+ 35 °)
=120 °
理由: ∵点O是△ABC的内心,
(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。
在△OBC中,
∠BOC =180 °-( ∠1+ ∠3 )
·
B
D
E
F
O
C
A
如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
解:设△ABC的内切圆与三边相切于D、E、F,
连结OA、OB、OC、OD、OE、OF,
则OD⊥AB,OE⊥BC,OF⊥AC.
∴S△ABC=S△AOB+S△BOC +S△AOC
设△ABC的三边为a、b、c,面积为S,
则△ABC的内切圆的半径 r=
三角形的内切圆的有关计算
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙O为Rt△ABC的内切圆. (1)求Rt△ABC的内切圆的半径 . (2)若移动点O的位置,使⊙O保持与△ABC的边AC、BC都相切,求⊙O的半径r的取值范围。
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:(1)设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
解得
r=1
在Rt△ABC中,BC=3,AC=4, ∴AB=5
由已知可得四边形ODCE为正方形,∴CD=CE=OD
∴ Rt△ABC的内切圆的半径为1。
(2)如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连结OB、OD,则四边形BODC为正方形。
·
A
B
O
D
C
∴OB=BC=3
∴半径r的取值范围为0<r≤3
几何问题代数化是解决几何问题的一种重要方法。
.
A
B
C
直角三角形的两直角边分别是5cm,12cm .则其内切圆的半径为______。
O
2cm
在△ABC中,∠C=90°,BC=3,AC=4.求这个三角形的外接圆半径和内切圆半径.
B
解:如图:由勾股定理可得:
O
∴外接圆半径R=2.5
由我们推导的三角形的面积公式可知:
解得:r=1
r
小结: 三角形的内切圆
(1)三角形的内心是三角形内切圆的圆心
(2)三角形的内心是三角形各角平分线的交点
(3)三角形内心到三边的距离相等
(4)三角形面积
(C为三角形周长,r为内切圆半径)
(5)直角三角形 的内切圆的半径为r 与 各边长 a、b、c的关系是
或
2、菱形ABCD中,周长为40,∠ABC=120°,则内切圆的半径为( )
3、如图,⊙O是△ABC的内切圆,
D、E、F是切点,∠A=50°,∠C=60°,
则∠DOE=( )
(A)70° (B)110°
(C)120° (D)130°
(A)梯形 (B)菱形 (C)矩形 (D)平行四边形
1、下列图形中,一定有内切圆的四边形是( )
B
B
D
4、等边三角形的内切圆半径、外接圆的半径和高的比为( )
5、存在内切圆和外接圆的四边形一定是( )
(A)矩形 (B)菱形
(C)正方形 (D)平行四边形
D
C
6.已知:△ABC的内切圆分别和BC、AC、AB相切于点D、E、F,∠DIE=120°,∠EIF=130°.求△ABC的三个内角的度数.
7.如图,△ABC中,E是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DE=DB
1
2
3
4
5
DB ? = AD · DF .
F
