19.2.3 一次函数与方程、不等式同步测试题(含解析)
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式同步测试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 11:14:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2019-2020学年八年级下学期
19.2.3一次函数与方程、不等式
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.如果每盒圆珠笔有12枝,售价18元,那么圆珠笔的销售额(元)与园珠笔的销售枝数x之间的函数关系式是( )
A. B. C. D.
2.若一次函数y=2x+6与y=kx的图象的交点纵坐标为4,则k的值是( )
A.-4 B.-2 C.2 D.4
3.一次函数与图像交点的横坐标是( )
A.4 B.2 C.1 D.0
6.一次函数y-kx+b的图象如图所示,则k,b的符号( )
A.k<0, b>0. B. k>0, b>0. C.k<0,b<0. D.k>0, b<0.
5.小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程中离家的距离s(米)与散步所用时间(分)之间的函数关系,根据图象,下列信息错误的是( )
A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
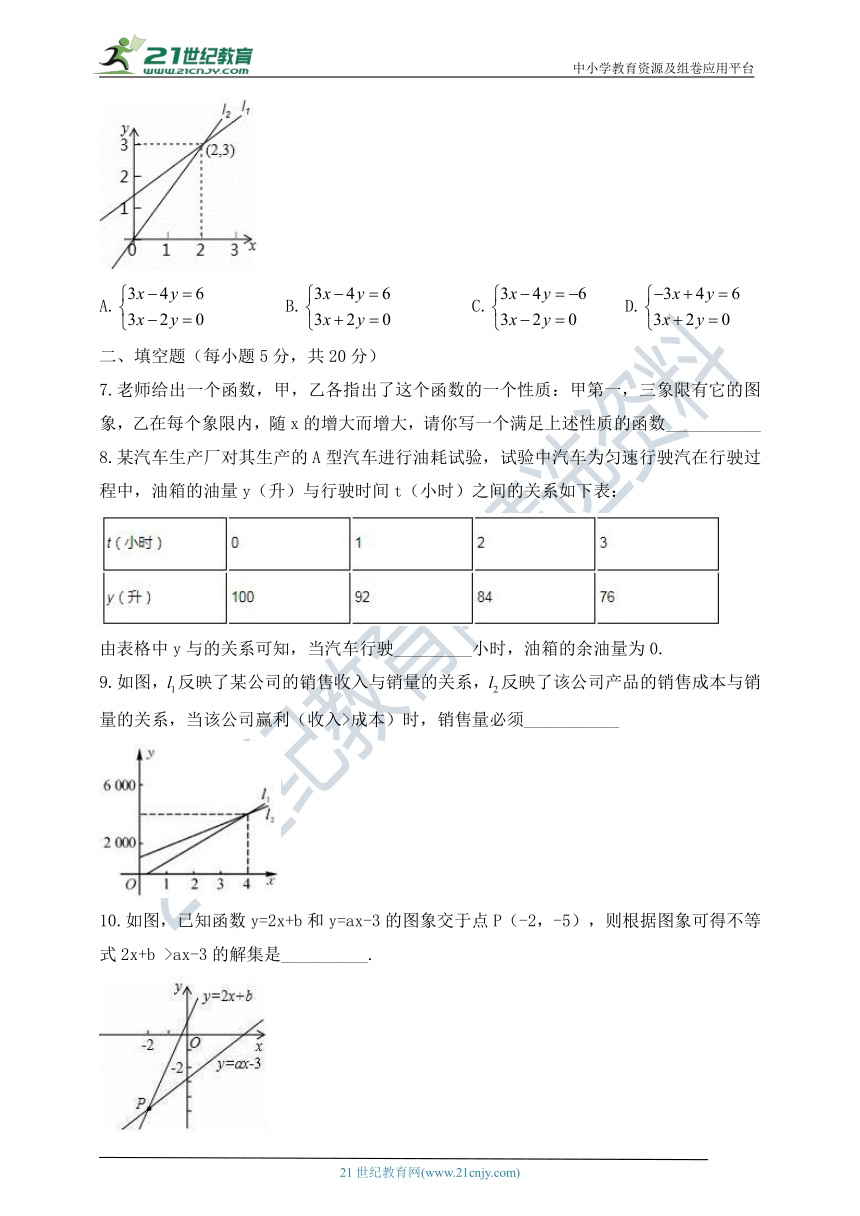
6.如图,以两条直线的交点坐标为解的方程组是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
7.老师给出一个函数,甲,乙各指出了这个函数的一个性质:甲第一,三象限有它的图象,乙在每个象限内,随x的增大而增大,请你写一个满足上述性质的函数___________
8.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的油量y(升)与行驶时间t(小时)之间的关系如下表:
由表格中y与的关系可知,当汽车行驶_________小时,油箱的余油量为0.
9.如图,反映了某公司的销售收入与销量的关系,反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入>成本)时,销售量必须___________
10.如图,已知函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b >ax-3的解集是__________.
三、解答题(共5题,共50分)
11.等腰三角形周长为10cm,底边BC长为ycm,腰AB长为xcm,写出y关于x的函数关系式.
12.一根祝寿蜡烛长85 cm,点燃时每小时缩短5cm.
(1)请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间(h)之间的函数关系式:
(2)请你预测该蜡烛可点燃多长时间?
13.一水库的水位在最近5小时之内持续上涨,下表记录了这5个小时水位高度
(1)由记录表推出这5个小时中水位高度y(单位:米)随时间(单位:时)变化的函数解析式,并在图画出该函数图象;
(2)据估计按这种上涨规律还会持续若干个小时,请预测再过多少小时水位高度将达到10.35米?
14.如图,图象描述了一汽车在某一直路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(时)之间的变量关系,根据图中提供的信息,填空:
①汽车离出发地最远是_________千米
②汽车在行驶途中停留了_________小时;
③汽车从出发地到回到原地共用了_________小时
15.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价30元,乒乓球每盒定价5元,现两家商店搞促销活动,甲店:每买一副球拍赠一盒乒乓球;乙店:按定价的9折优惠,某班级需购球拍4付,乒乓球若干盒(不少于4盒)
(1)设购买乒乓球盒数为x(盒),在甲店购买的付款数为y(元),在乙店购买的付款数为y(元),分别写出在两家商店购买的付款数与乒乓球盒数x之间的函数关系式;
(2)就乒乓球盒数讨论去哪家商店买合算?
答案
1.【解析】A
2.【解析】A。一次函数y=2x+6与y=kx图象的交点纵坐标为4,
所以4=2x+6解得:x=-1,
所以交点坐标为(-1,4),
代入y=kx,4=-k,
解得k=-4.
3.【解析】C
4.【解析】A
5.【解析】A
6.【解析】C。根据给出的函数所经过的点的坐标:(2.3),(0,0);
3分别求出图中直线的解析式为y=x,再把(2,3)代入方程,因此所求的二元一次方程组是
7.【解析】y=x+1
8.【解析】12.5。由题意可得:y= 100-8t,当y=0时,0=100-8t解得:t= 12.5
9.【解析】大于4
10.【解析】函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b> ax-3的解集是x>-2
11.【解析】
12.【解析】(1)因为蜡烛的长等于蜡烛的原长减去燃烧的长度,所以y=85-5t;
(2)因为蜡烛燃 的时候蜡烛的长度y=0.
所以85-5t=0解得t=17.
所以该蜡烛可点燃17小时、
13.【解析】(1)设函数的解析式为y=kt+b,由记录表得:,解得,函数的解析式为:y=0.05t+10
列表为:
描点并连线为:
(2)当y=10.35时,10.35=0.05t+10解得t=7
所以再过2小时水位高度将达到10.35米.
14.【解析】①100 ②0.5 ③4.5
15.【解析】解:(1)由题意,得
(2)当y=y时,即100+5x-4.5x+108,解得x-16,到两店价格一样;当y>y时,即100+5x > 4.5x+108,解得x> 16,到乙店合算;当y_21?????????è?????(www.21cnjy.com)_
人教版2019-2020学年八年级下学期
19.2.3一次函数与方程、不等式
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.如果每盒圆珠笔有12枝,售价18元,那么圆珠笔的销售额(元)与园珠笔的销售枝数x之间的函数关系式是( )
A. B. C. D.
2.若一次函数y=2x+6与y=kx的图象的交点纵坐标为4,则k的值是( )
A.-4 B.-2 C.2 D.4
3.一次函数与图像交点的横坐标是( )
A.4 B.2 C.1 D.0
6.一次函数y-kx+b的图象如图所示,则k,b的符号( )
A.k<0, b>0. B. k>0, b>0. C.k<0,b<0. D.k>0, b<0.
5.小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程中离家的距离s(米)与散步所用时间(分)之间的函数关系,根据图象,下列信息错误的是( )
A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
6.如图,以两条直线的交点坐标为解的方程组是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
7.老师给出一个函数,甲,乙各指出了这个函数的一个性质:甲第一,三象限有它的图象,乙在每个象限内,随x的增大而增大,请你写一个满足上述性质的函数___________
8.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的油量y(升)与行驶时间t(小时)之间的关系如下表:
由表格中y与的关系可知,当汽车行驶_________小时,油箱的余油量为0.
9.如图,反映了某公司的销售收入与销量的关系,反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入>成本)时,销售量必须___________
10.如图,已知函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b >ax-3的解集是__________.
三、解答题(共5题,共50分)
11.等腰三角形周长为10cm,底边BC长为ycm,腰AB长为xcm,写出y关于x的函数关系式.
12.一根祝寿蜡烛长85 cm,点燃时每小时缩短5cm.
(1)请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间(h)之间的函数关系式:
(2)请你预测该蜡烛可点燃多长时间?
13.一水库的水位在最近5小时之内持续上涨,下表记录了这5个小时水位高度
(1)由记录表推出这5个小时中水位高度y(单位:米)随时间(单位:时)变化的函数解析式,并在图画出该函数图象;
(2)据估计按这种上涨规律还会持续若干个小时,请预测再过多少小时水位高度将达到10.35米?
14.如图,图象描述了一汽车在某一直路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(时)之间的变量关系,根据图中提供的信息,填空:
①汽车离出发地最远是_________千米
②汽车在行驶途中停留了_________小时;
③汽车从出发地到回到原地共用了_________小时
15.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价30元,乒乓球每盒定价5元,现两家商店搞促销活动,甲店:每买一副球拍赠一盒乒乓球;乙店:按定价的9折优惠,某班级需购球拍4付,乒乓球若干盒(不少于4盒)
(1)设购买乒乓球盒数为x(盒),在甲店购买的付款数为y(元),在乙店购买的付款数为y(元),分别写出在两家商店购买的付款数与乒乓球盒数x之间的函数关系式;
(2)就乒乓球盒数讨论去哪家商店买合算?
答案
1.【解析】A
2.【解析】A。一次函数y=2x+6与y=kx图象的交点纵坐标为4,
所以4=2x+6解得:x=-1,
所以交点坐标为(-1,4),
代入y=kx,4=-k,
解得k=-4.
3.【解析】C
4.【解析】A
5.【解析】A
6.【解析】C。根据给出的函数所经过的点的坐标:(2.3),(0,0);
3分别求出图中直线的解析式为y=x,再把(2,3)代入方程,因此所求的二元一次方程组是
7.【解析】y=x+1
8.【解析】12.5。由题意可得:y= 100-8t,当y=0时,0=100-8t解得:t= 12.5
9.【解析】大于4
10.【解析】函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b> ax-3的解集是x>-2
11.【解析】
12.【解析】(1)因为蜡烛的长等于蜡烛的原长减去燃烧的长度,所以y=85-5t;
(2)因为蜡烛燃 的时候蜡烛的长度y=0.
所以85-5t=0解得t=17.
所以该蜡烛可点燃17小时、
13.【解析】(1)设函数的解析式为y=kt+b,由记录表得:,解得,函数的解析式为:y=0.05t+10
列表为:
描点并连线为:
(2)当y=10.35时,10.35=0.05t+10解得t=7
所以再过2小时水位高度将达到10.35米.
14.【解析】①100 ②0.5 ③4.5
15.【解析】解:(1)由题意,得
(2)当y=y时,即100+5x-4.5x+108,解得x-16,到两店价格一样;当y>y时,即100+5x > 4.5x+108,解得x> 16,到乙店合算;当y
