五年级数学下册拓展课件-第1单元 简易方程-苏教版(共36张PPT)
文档属性
| 名称 | 五年级数学下册拓展课件-第1单元 简易方程-苏教版(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
提升拓展课件
江苏版五年级下
第1课时 等式与方程
看图列方程
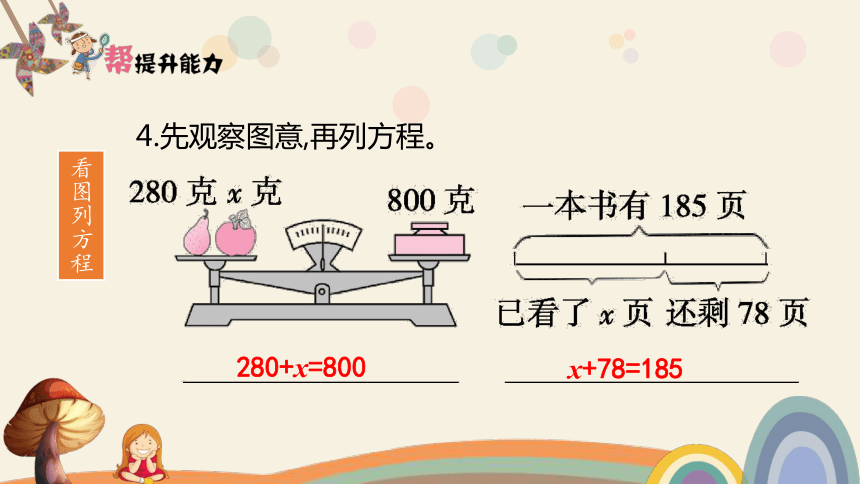
4.先观察图意,再列方程。
280+x=800
x+78=185
用方程表示等量关系
5.根据题意,先找等量关系,再列方程。
(1)每千克普通海水中含盐x克,亚洲与非洲之间的红海是世界上最咸的海,每千克海水中含盐41克,比普通海水的2倍少29克。
等量关系式为 .
,列方程为 。?
红海每千克海水含盐量=普通海水
每千克含盐量×2-29
2x-29=41
(2)哈雷彗星是人类首颗有记录的周期彗星,哈雷彗星上一次回归是在1986年,它每n年回归一次,经科学家推算它将在2061年再次回归。
等量关系式为 ,列方程
为 。?
1986年+n年=2061年
1986+n=2061
第2课时 等式的性质(1)和解方程
根据数量关系列方程并解答
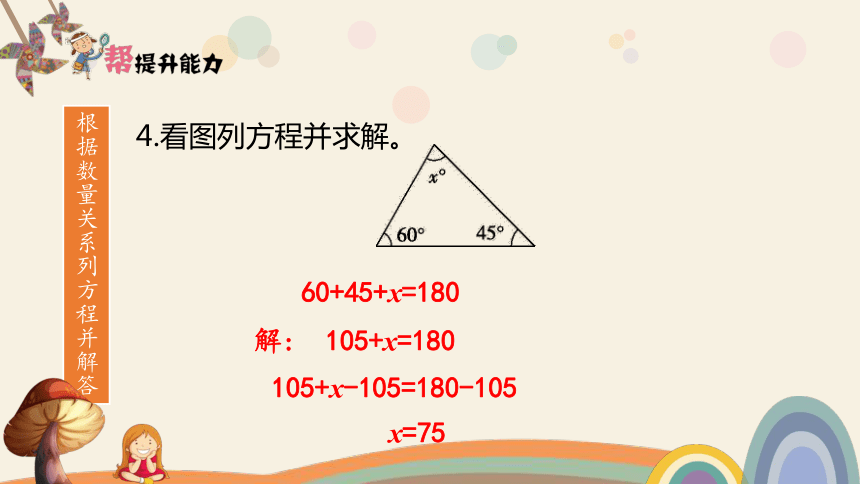
4.看图列方程并求解。
60+45+x=180
解: 105+x=180
105+x-105=180-105
x=75
5.四川凉山州木里县是四川森林面积第一的县,2019年3月30日发生火灾,发现时已有2公顷森林受灾,一小时后火灾面积达到15公顷。设这一小时火灾蔓延了x公顷,求x的值。(列方程解答)
2+x=15
解:2+x-2=15-2
x=13
运用等式的性质(1)
解决问题
6.“嫦娥四号”探测器是世界首个在月球背面软着陆和巡视探测的航天器。宇航员带了1本航天记录本和3支专用笔,这相当于6支专用笔的造价,设1本航天记录本的造价相当于x支专用笔的造价,求x的值。(列方程解答)
x+3=6
解:x+3-3=6-3
x=3
第3课时 等式的性质(2)和解方程
运用方程解决问题
4.列方程并求x,y的值。
14x=50.4
解:x=3.6
9.5y=76
解:y=8
物品名称 单 价 数 量 总 价
日记本 x元 14本 50.4元
钢 笔 9.5元 y支 76元
运用代入法解决有关
方程的问题
5.方程6x=1.8与m-x=2.4有相同的解,求m的值。
6x=1.8
解:x=0.3
把x=0.3代入m-x=2.4
m-0.3=2.4
解:m=2.7
第4课时 列一步计算的方程解决实际问题
进一步运用列一步计算的
方程解决实际问题
3.蓖麻的种子中存有一种称为蓖麻青的毒素,100克这样的毒素就足以使成人致命,成人误食20粒可导致中毒死亡。每粒蓖麻籽含毒素多少克?
解:设每粒蓖麻籽含毒素x克。
20x=100
x=5
答:每粒蓖麻籽含毒素5克。
方程与几何的综合运用
4.如下图,已知长方形和正方形的面积相等,求长方形的宽是多少分米?
解:设长方形的宽为x dm。
32x=16×16
x=8
答:长方形的宽是8 dm。
第5课时 列两步计算的方程解决实际问题(1)
运用画线段图的方法
找等量关系
3.长江是我国最长的河,全长约6300千米,比珠江全长的2倍还长1660千米。珠江全长约多少千米?
(1)根据题意,画线段图。
1660
(2)等量关系式:( )×2+1660=( )全长。
(3)解:设( )。
(4)列方程并解方程:
珠江全长
长江
2x+1660=6300
珠江全长约x千米
x=2320
运用不同的等量关系式
列方程解实际问题
4.列方程解答问题。
(1)青藏铁路全长1956千米,比山东胶济铁路的4倍还多384千米。山东胶济铁路全长多少千米?
设( )。
根据青藏铁路全长与山东胶济铁路全长之间的关系可列出下面的等量关系式。
山东胶济铁路全长x千米
①( )铁路全长×4+384=( )铁路全长。
列方程并解方程:
山东胶济
青藏
解: x=393
4x+384=1956
②( )铁路全长-( )铁路全长
×4=384。
列方程并解方程:
青藏
山东胶济
解:x=393
1956-4x=384
③( )铁路全长×4=青藏铁路全长
( )384。
列方程并解方程:
山东胶济
-
解:x=393
4x=1956-384
(2)蓝鲸亦称“剃刀鲸”,是目前最大的鲸类,也是现存最大的动物,一条舌头就有2000千克,比一名成年男子体重的14倍少100千克,一名成年男子的体重是多少千克?(请你用两种不同的等量关系式来列方程并解答)
解:设一名成年男子的体重为x千克。
一名成年男子的体重×14-100=蓝鲸的舌头重
x=150
14x-100=2000
一名成年男子的体重×14=蓝鲸的舌头重+100
x=150
14x=2000+100
答:一名成年男子的体重是150千克。
第6课时 列两步计算的方程解决实际问题(2)
列形如ax÷b=c(b≠0)的
方程解决实际问题
3.先写等量关系式,再列方程求x的值。
(1)李叔叔家有一块面积为500平方米的梯形苗圃,它的上下底之和为20米,它的高为x米。
等量关系式: 。
列方程并解方程:
梯形的上下底之和×高÷2=梯形的面积
20x÷2=500
解:x=50
(2)一块三角形布料底边长为10分米,面积为40平方分米,该底上的高为x分米。
等量关系式: 。?
列方程并解方程:
三角形的底×高÷2=三角形的面积
10x÷2=40
解:x=8
运用转化法解决结果
等于0的问题
4.当a等于什么数时,式子(8-5a)÷3的结果是0?
(8-5a)÷3=0
解:(8-5a)÷3×3=0×3
8-5a=0
8-5a+5a=0+5a
8=5a
5a÷5=8÷5
a=1.6
5.当a等于什么数时,式子(3a-2)÷4的结果是1?
(3a-2)÷4=1
解:(3a-2)÷4×4=1×4
3a-2+2=4+2
3a-2=4
3a=6
3a÷3=6÷3
a=2
第7课时 列方程解决简单的实际问题
列方程解决连续整数的问题
4.三个连续的奇数和为27,求这三个连续奇数各是多少。
解:设中间的一个奇数为x,则它前面的一个奇数为(x-2),后面的一个奇数为(x+2)。
(x-2)+x+(x+2)=27
3x=27
3x÷3=27÷3
x=9
9-2=7 9+2=11
答:这三个连续奇数分别是7,9,11。
运用抓不变量法解决问题
5.华华今年9岁,爸爸今年35岁,华华多少岁时,爸爸的年龄是华华的3倍?
解:设华华x岁,爸爸的年龄为3x岁。
3x-x=35-9
2x=26
2x÷2=26÷2
x=13
答:华华13岁时,爸爸的年龄是华华的3倍。
第8课时 列方程解决稍复杂的实际问题
根据线段图列方程
2.看线段图列方程求解。
3x+14×2=64
解: 3x+28=64
3x+28-28=64-28
3x=36
3x÷3=36÷3
x=12
进一步应用ax±bc=d
的方程解决问题
3.王老师买了一些文具用品,票据单被撕掉了一部分,你能帮他计算一下每本笔记本的价钱吗?
解:设每本笔记本的价钱为x元。
25x+15×12=267.5
25x+180-180=267.5-180
25x=87.5
25x÷25=87.5÷25
x=3.5
答:每本笔记本的价钱为3.5元。
谢谢观赏
谢谢观赏
谢谢观赏
提升拓展课件
江苏版五年级下
第1课时 等式与方程
看图列方程
4.先观察图意,再列方程。
280+x=800
x+78=185
用方程表示等量关系
5.根据题意,先找等量关系,再列方程。
(1)每千克普通海水中含盐x克,亚洲与非洲之间的红海是世界上最咸的海,每千克海水中含盐41克,比普通海水的2倍少29克。
等量关系式为 .
,列方程为 。?
红海每千克海水含盐量=普通海水
每千克含盐量×2-29
2x-29=41
(2)哈雷彗星是人类首颗有记录的周期彗星,哈雷彗星上一次回归是在1986年,它每n年回归一次,经科学家推算它将在2061年再次回归。
等量关系式为 ,列方程
为 。?
1986年+n年=2061年
1986+n=2061
第2课时 等式的性质(1)和解方程
根据数量关系列方程并解答
4.看图列方程并求解。
60+45+x=180
解: 105+x=180
105+x-105=180-105
x=75
5.四川凉山州木里县是四川森林面积第一的县,2019年3月30日发生火灾,发现时已有2公顷森林受灾,一小时后火灾面积达到15公顷。设这一小时火灾蔓延了x公顷,求x的值。(列方程解答)
2+x=15
解:2+x-2=15-2
x=13
运用等式的性质(1)
解决问题
6.“嫦娥四号”探测器是世界首个在月球背面软着陆和巡视探测的航天器。宇航员带了1本航天记录本和3支专用笔,这相当于6支专用笔的造价,设1本航天记录本的造价相当于x支专用笔的造价,求x的值。(列方程解答)
x+3=6
解:x+3-3=6-3
x=3
第3课时 等式的性质(2)和解方程
运用方程解决问题
4.列方程并求x,y的值。
14x=50.4
解:x=3.6
9.5y=76
解:y=8
物品名称 单 价 数 量 总 价
日记本 x元 14本 50.4元
钢 笔 9.5元 y支 76元
运用代入法解决有关
方程的问题
5.方程6x=1.8与m-x=2.4有相同的解,求m的值。
6x=1.8
解:x=0.3
把x=0.3代入m-x=2.4
m-0.3=2.4
解:m=2.7
第4课时 列一步计算的方程解决实际问题
进一步运用列一步计算的
方程解决实际问题
3.蓖麻的种子中存有一种称为蓖麻青的毒素,100克这样的毒素就足以使成人致命,成人误食20粒可导致中毒死亡。每粒蓖麻籽含毒素多少克?
解:设每粒蓖麻籽含毒素x克。
20x=100
x=5
答:每粒蓖麻籽含毒素5克。
方程与几何的综合运用
4.如下图,已知长方形和正方形的面积相等,求长方形的宽是多少分米?
解:设长方形的宽为x dm。
32x=16×16
x=8
答:长方形的宽是8 dm。
第5课时 列两步计算的方程解决实际问题(1)
运用画线段图的方法
找等量关系
3.长江是我国最长的河,全长约6300千米,比珠江全长的2倍还长1660千米。珠江全长约多少千米?
(1)根据题意,画线段图。
1660
(2)等量关系式:( )×2+1660=( )全长。
(3)解:设( )。
(4)列方程并解方程:
珠江全长
长江
2x+1660=6300
珠江全长约x千米
x=2320
运用不同的等量关系式
列方程解实际问题
4.列方程解答问题。
(1)青藏铁路全长1956千米,比山东胶济铁路的4倍还多384千米。山东胶济铁路全长多少千米?
设( )。
根据青藏铁路全长与山东胶济铁路全长之间的关系可列出下面的等量关系式。
山东胶济铁路全长x千米
①( )铁路全长×4+384=( )铁路全长。
列方程并解方程:
山东胶济
青藏
解: x=393
4x+384=1956
②( )铁路全长-( )铁路全长
×4=384。
列方程并解方程:
青藏
山东胶济
解:x=393
1956-4x=384
③( )铁路全长×4=青藏铁路全长
( )384。
列方程并解方程:
山东胶济
-
解:x=393
4x=1956-384
(2)蓝鲸亦称“剃刀鲸”,是目前最大的鲸类,也是现存最大的动物,一条舌头就有2000千克,比一名成年男子体重的14倍少100千克,一名成年男子的体重是多少千克?(请你用两种不同的等量关系式来列方程并解答)
解:设一名成年男子的体重为x千克。
一名成年男子的体重×14-100=蓝鲸的舌头重
x=150
14x-100=2000
一名成年男子的体重×14=蓝鲸的舌头重+100
x=150
14x=2000+100
答:一名成年男子的体重是150千克。
第6课时 列两步计算的方程解决实际问题(2)
列形如ax÷b=c(b≠0)的
方程解决实际问题
3.先写等量关系式,再列方程求x的值。
(1)李叔叔家有一块面积为500平方米的梯形苗圃,它的上下底之和为20米,它的高为x米。
等量关系式: 。
列方程并解方程:
梯形的上下底之和×高÷2=梯形的面积
20x÷2=500
解:x=50
(2)一块三角形布料底边长为10分米,面积为40平方分米,该底上的高为x分米。
等量关系式: 。?
列方程并解方程:
三角形的底×高÷2=三角形的面积
10x÷2=40
解:x=8
运用转化法解决结果
等于0的问题
4.当a等于什么数时,式子(8-5a)÷3的结果是0?
(8-5a)÷3=0
解:(8-5a)÷3×3=0×3
8-5a=0
8-5a+5a=0+5a
8=5a
5a÷5=8÷5
a=1.6
5.当a等于什么数时,式子(3a-2)÷4的结果是1?
(3a-2)÷4=1
解:(3a-2)÷4×4=1×4
3a-2+2=4+2
3a-2=4
3a=6
3a÷3=6÷3
a=2
第7课时 列方程解决简单的实际问题
列方程解决连续整数的问题
4.三个连续的奇数和为27,求这三个连续奇数各是多少。
解:设中间的一个奇数为x,则它前面的一个奇数为(x-2),后面的一个奇数为(x+2)。
(x-2)+x+(x+2)=27
3x=27
3x÷3=27÷3
x=9
9-2=7 9+2=11
答:这三个连续奇数分别是7,9,11。
运用抓不变量法解决问题
5.华华今年9岁,爸爸今年35岁,华华多少岁时,爸爸的年龄是华华的3倍?
解:设华华x岁,爸爸的年龄为3x岁。
3x-x=35-9
2x=26
2x÷2=26÷2
x=13
答:华华13岁时,爸爸的年龄是华华的3倍。
第8课时 列方程解决稍复杂的实际问题
根据线段图列方程
2.看线段图列方程求解。
3x+14×2=64
解: 3x+28=64
3x+28-28=64-28
3x=36
3x÷3=36÷3
x=12
进一步应用ax±bc=d
的方程解决问题
3.王老师买了一些文具用品,票据单被撕掉了一部分,你能帮他计算一下每本笔记本的价钱吗?
解:设每本笔记本的价钱为x元。
25x+15×12=267.5
25x+180-180=267.5-180
25x=87.5
25x÷25=87.5÷25
x=3.5
答:每本笔记本的价钱为3.5元。
谢谢观赏
谢谢观赏
谢谢观赏
