北师大版八年级数学下册2.5. 1一元一次不等式与一次函数课件 (共21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册2.5. 1一元一次不等式与一次函数课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 599.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
2.5.1一元一次不等式
与一次函数
北师大版八年级数学下册第二章第五节第1课时
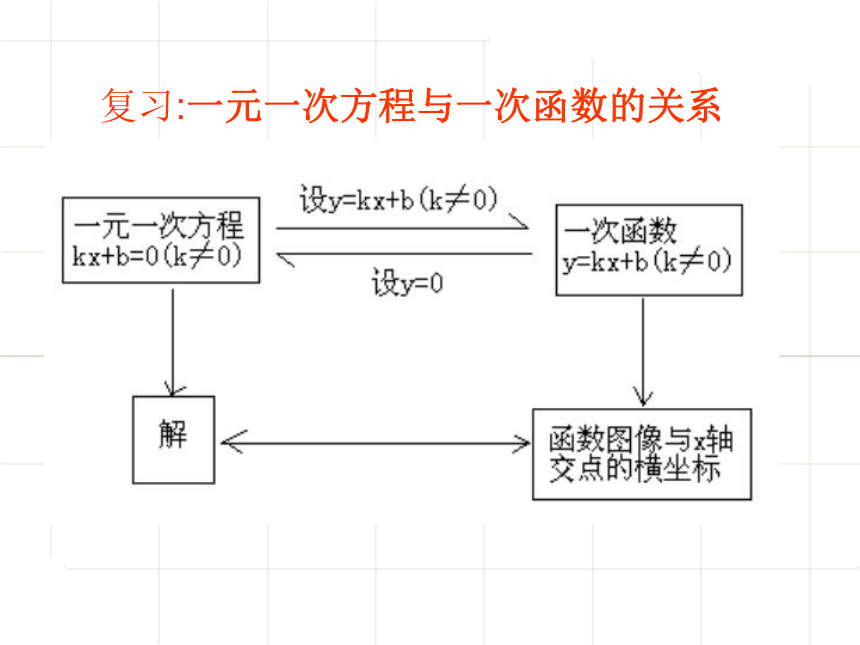
复习:一元一次方程与一次函数的关系
自主学习 ,探究新知
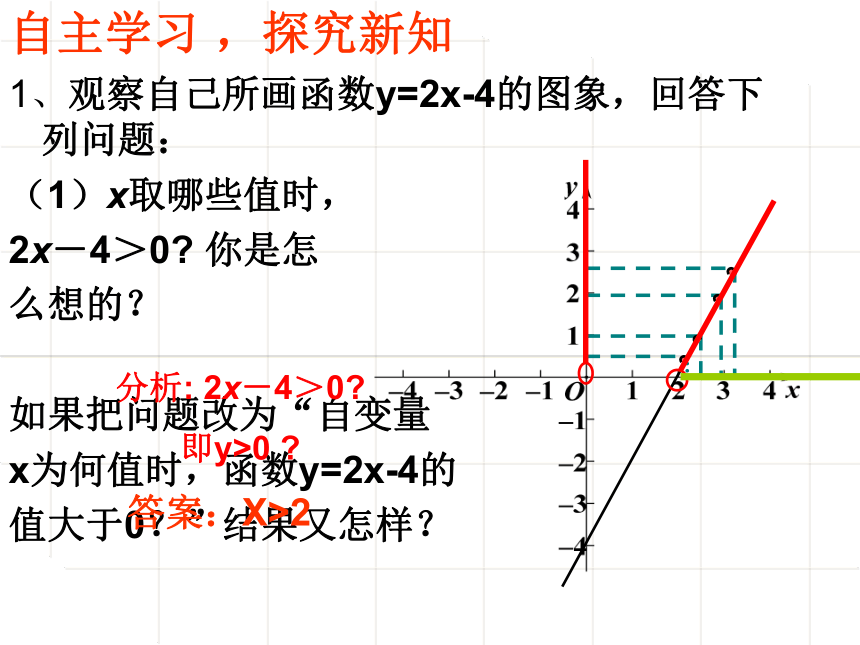
1、观察自己所画函数y=2x-4的图象,回答下列问题:
(1)x取哪些值时,
2x-4>0? 你是怎
么想的?
如果把问题改为“自变量
x为何值时,函数y=2x-4的
值大于0?”结果又怎样?
答案:X>2
分析: 2x-4>0?
即y>0 ?
自主学习 ,探究新知
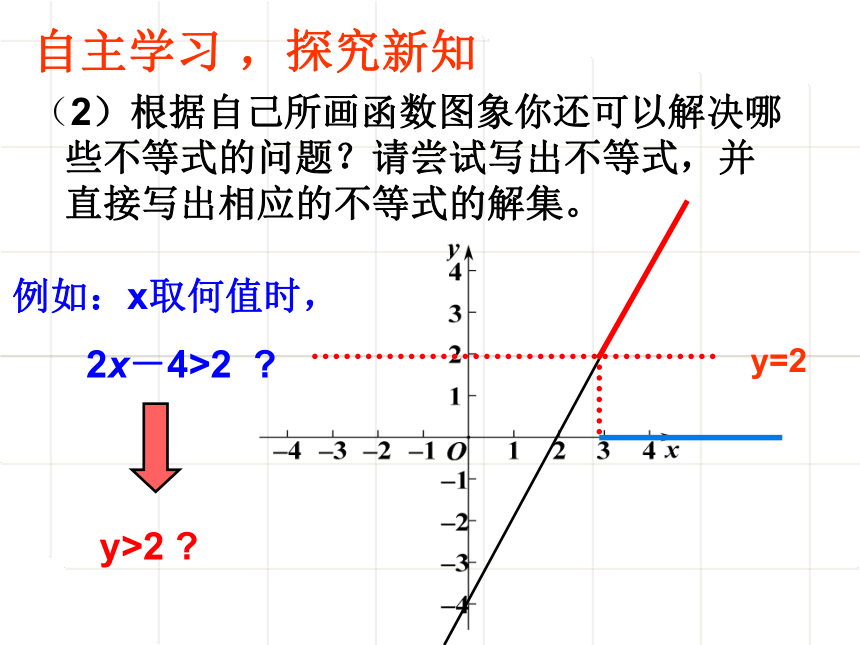
(2)根据自己所画函数图象你还可以解决哪些不等式的问题?请尝试写出不等式,并直接写出相应的不等式的解集。
例如:x取何值时,
2x-4>2 ?
y=2
y>2 ?
①整体与部分的关系
从图象看,一次函数用 表示,一元一次方程用 表示,一元一次不等式用 表示,说明方程、不等式可以看作是函数图象上的一部分。
小结:一元一次不等式与一次函数的关系
直线
点
射线
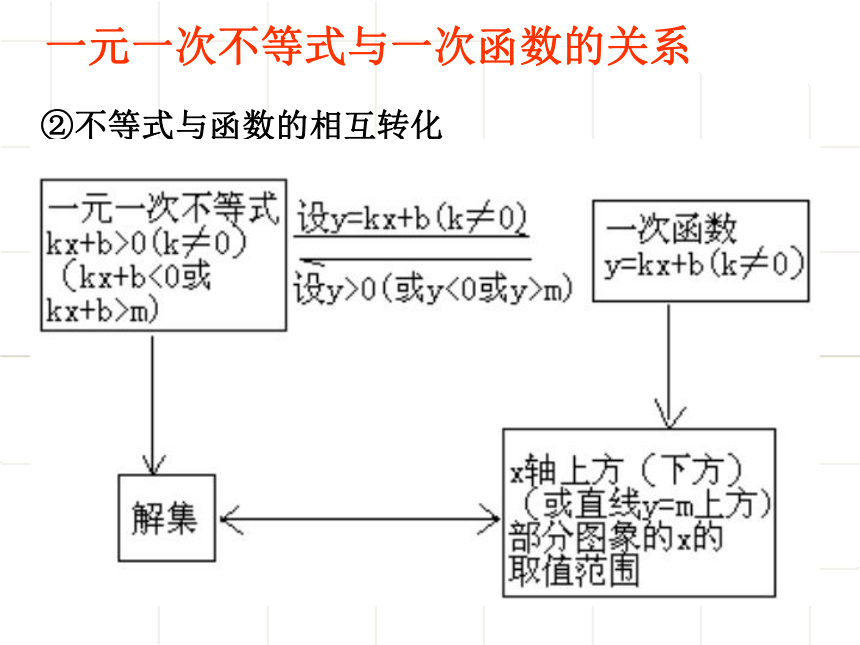
一元一次不等式与一次函数的关系
②不等式与函数的相互转化
自主学习 ,探究新知
3、小试牛刀
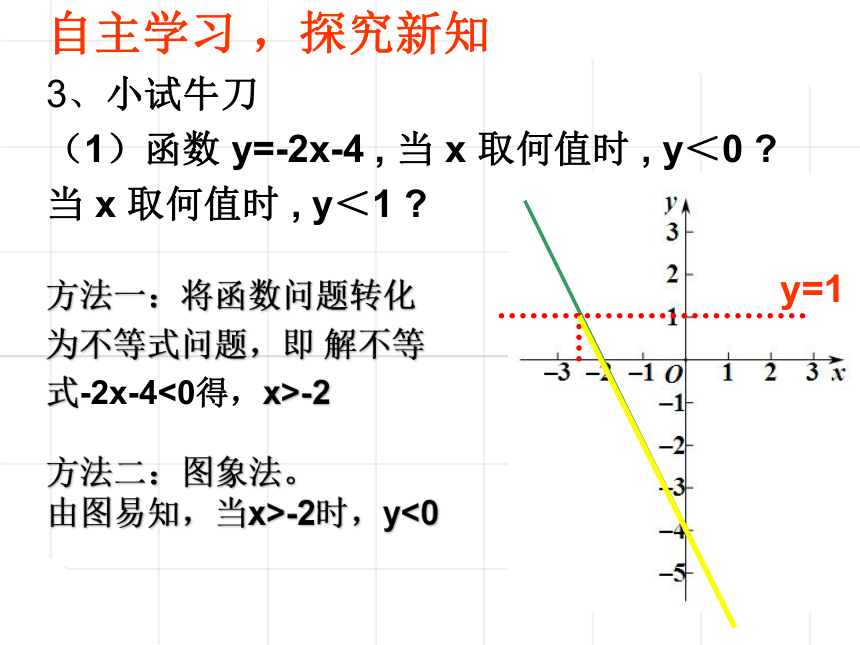
(1)函数 y=-2x-4 , 当 x 取何值时 , y<0 ?
当 x 取何值时 , y<1 ?
方法一:将函数问题转化
为不等式问题,即 解不等
式-2x-4<0得,x>-2
方法二:图象法。
由图易知,当x>-2时,y<0
y=1
自主学习 ,探究新知
3、小试牛刀
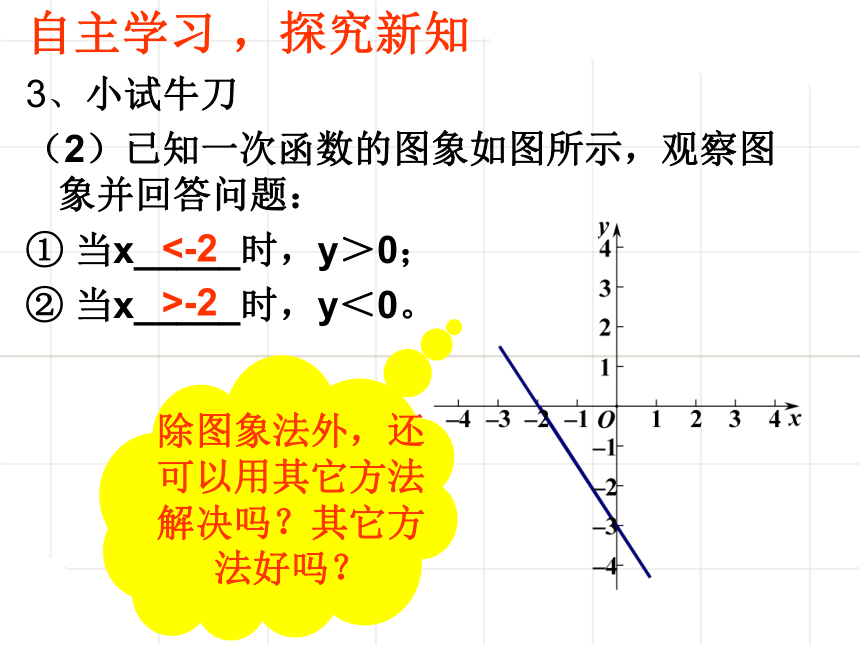
(2)已知一次函数的图象如图所示,观察图象并回答问题:
① 当x_____时,y>0;
② 当x_____时,y<0。
>-2
<-2
问题解决,深化新知
阅读下面的材料,完成后面的问题。
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,画出函数图象,观察图象回答下列问题:
① 何时哥哥追上弟弟?
② 何时弟弟跑在哥哥前面?
③ 何时哥哥跑在弟弟前面?
④ 谁先跑过20m?谁先跑过100m?
⑤ 你是怎样求解的?与同伴交流。
解:设x 为哥哥起跑开始的时间, 则哥哥与弟弟每人所跑的距离 y (m)与时间 x (s) 之间的关系式分别是:
思路一:图象法
哥哥追上弟弟;
(2) 弟弟跑
在哥哥前面;
(3) 哥哥跑在弟
弟前面;
9s时
0sX>9s时
(4) 先跑过 20米,
先跑过 100米 。
弟弟
哥哥
思路二:代数法
哥哥: y1=4x
弟弟: y2=3x+9
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
4x<3x+9
04x>3x+9
x>9
4x=20
3x+9=20
x=5
4x=100
3x+9=100
x=25
∴弟弟先跑过20m
∴哥哥先跑过100m
(1)何时哥哥追上弟弟?
4x=3x+9
X=9
问题解决,深化新知
2、挑战自我
已知 , ,当 x取哪些值时, ? 你有哪些不同的解决方法?
问题解决,深化新知
2、挑战自我
解法二:分别画出函数 和 的图象
问题解决,深化新知
2、挑战自我
解法三:把不等式-x+3>3x-4化为4x-7<0
设y=4x-7,画出函数y=4x-7的图象,观察图象可得
归纳反思,内化新知
1、一次函数与一元一次不等式的关系结构图
(“数”与“形”的互相转化)
2、本课渗透的数学思想:
(1)数形结合思想
(2)化归思想
达标测评,反馈新知
1、一次函数y=3x-7在x轴下方的图象的x的取值范围是 。
2、已知一次函数y=-5x-3,当x______时,y>2。
<-1
达标测评,反馈新知
3、
观察图像直接写出不等式kx+b≥0的
解集为 。
X≥-3
达标测评,反馈新知
4、某图书馆开展两种方式的租书业务,一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书的金额y(元)与租书时间x(天)之间的关系如图所示:观察图象,使用会员卡、租书卡,这两种卡在什么情况下合算?
当0当x=100时,两种卡一样合算
当X>100时,会员卡合算
布置作业,延伸新知
1.必做题:书本P51第1、2、3题;
2.选做题:书本P51第4题;
拓展题:函数 y=-2x-4 , 当 x 取何值时 ,
1谢谢同学们!
同学们再见!
2.5.1一元一次不等式
与一次函数
北师大版八年级数学下册第二章第五节第1课时
复习:一元一次方程与一次函数的关系
自主学习 ,探究新知
1、观察自己所画函数y=2x-4的图象,回答下列问题:
(1)x取哪些值时,
2x-4>0? 你是怎
么想的?
如果把问题改为“自变量
x为何值时,函数y=2x-4的
值大于0?”结果又怎样?
答案:X>2
分析: 2x-4>0?
即y>0 ?
自主学习 ,探究新知
(2)根据自己所画函数图象你还可以解决哪些不等式的问题?请尝试写出不等式,并直接写出相应的不等式的解集。
例如:x取何值时,
2x-4>2 ?
y=2
y>2 ?
①整体与部分的关系
从图象看,一次函数用 表示,一元一次方程用 表示,一元一次不等式用 表示,说明方程、不等式可以看作是函数图象上的一部分。
小结:一元一次不等式与一次函数的关系
直线
点
射线
一元一次不等式与一次函数的关系
②不等式与函数的相互转化
自主学习 ,探究新知
3、小试牛刀
(1)函数 y=-2x-4 , 当 x 取何值时 , y<0 ?
当 x 取何值时 , y<1 ?
方法一:将函数问题转化
为不等式问题,即 解不等
式-2x-4<0得,x>-2
方法二:图象法。
由图易知,当x>-2时,y<0
y=1
自主学习 ,探究新知
3、小试牛刀
(2)已知一次函数的图象如图所示,观察图象并回答问题:
① 当x_____时,y>0;
② 当x_____时,y<0。
>-2
<-2
问题解决,深化新知
阅读下面的材料,完成后面的问题。
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,画出函数图象,观察图象回答下列问题:
① 何时哥哥追上弟弟?
② 何时弟弟跑在哥哥前面?
③ 何时哥哥跑在弟弟前面?
④ 谁先跑过20m?谁先跑过100m?
⑤ 你是怎样求解的?与同伴交流。
解:设x 为哥哥起跑开始的时间, 则哥哥与弟弟每人所跑的距离 y (m)与时间 x (s) 之间的关系式分别是:
思路一:图象法
哥哥追上弟弟;
(2) 弟弟跑
在哥哥前面;
(3) 哥哥跑在弟
弟前面;
9s时
0s
(4) 先跑过 20米,
先跑过 100米 。
弟弟
哥哥
思路二:代数法
哥哥: y1=4x
弟弟: y2=3x+9
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
4x<3x+9
0
x>9
4x=20
3x+9=20
x=5
4x=100
3x+9=100
x=25
∴弟弟先跑过20m
∴哥哥先跑过100m
(1)何时哥哥追上弟弟?
4x=3x+9
X=9
问题解决,深化新知
2、挑战自我
已知 , ,当 x取哪些值时, ? 你有哪些不同的解决方法?
问题解决,深化新知
2、挑战自我
解法二:分别画出函数 和 的图象
问题解决,深化新知
2、挑战自我
解法三:把不等式-x+3>3x-4化为4x-7<0
设y=4x-7,画出函数y=4x-7的图象,观察图象可得
归纳反思,内化新知
1、一次函数与一元一次不等式的关系结构图
(“数”与“形”的互相转化)
2、本课渗透的数学思想:
(1)数形结合思想
(2)化归思想
达标测评,反馈新知
1、一次函数y=3x-7在x轴下方的图象的x的取值范围是 。
2、已知一次函数y=-5x-3,当x______时,y>2。
<-1
达标测评,反馈新知
3、
观察图像直接写出不等式kx+b≥0的
解集为 。
X≥-3
达标测评,反馈新知
4、某图书馆开展两种方式的租书业务,一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书的金额y(元)与租书时间x(天)之间的关系如图所示:观察图象,使用会员卡、租书卡,这两种卡在什么情况下合算?
当0
当X>100时,会员卡合算
布置作业,延伸新知
1.必做题:书本P51第1、2、3题;
2.选做题:书本P51第4题;
拓展题:函数 y=-2x-4 , 当 x 取何值时 ,
1
同学们再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
