沪科版八年级数学下册:17.2.1直接开平方法 复习学案(无答案)
文档属性
| 名称 | 沪科版八年级数学下册:17.2.1直接开平方法 复习学案(无答案) | 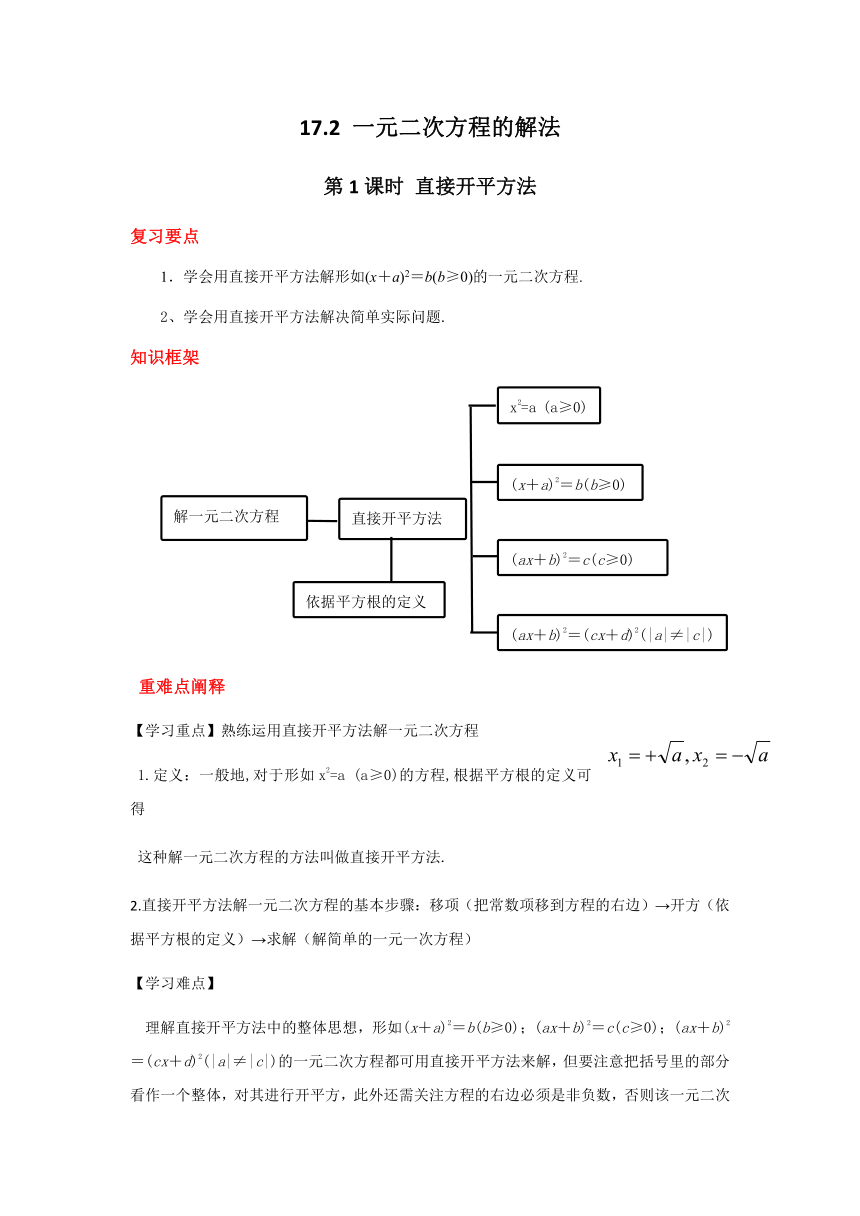 | |
| 格式 | zip | ||
| 文件大小 | 28.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 05:59:21 | ||
图片预览


文档简介
17.2 一元二次方程的解法
第1课时 直接开平方法
复习要点
1.学会用直接开平方法解形如(x+a)2=b(b≥0)的一元二次方程.
2、学会用直接开平方法解决简单实际问题.
知识框架
重难点阐释
【学习重点】熟练运用直接开平方法解一元二次方程
1.定义:一般地,对于形如x2=a (a≥0)的方程,根据平方根的定义可得
这种解一元二次方程的方法叫做直接开平方法.
2.直接开平方法解一元二次方程的基本步骤:移项(把常数项移到方程的右边)→开方(依据平方根的定义)→求解(解简单的一元一次方程)
【学习难点】
理解直接开平方法中的整体思想,形如(x+a)2=b(b≥0);(ax+b)2=c(c≥0);(ax+b)2=(cx+d)2(|a|≠|c|)的一元二次方程都可用直接开平方法来解,但要注意把括号里的部分看作一个整体,对其进行开平方,此外还需关注方程的右边必须是非负数,否则该一元二次方程无实数根,不可用直接开平方法.
典例突破
例:用直接开平方法解下列方程:
(1)x2-16=0; (2)3x2-27=0;
(3)(x-2)2=9; (4)(2y-3)2=16.
解析:用直接开平方法解方程时,要先将方程化成左边是含未知数的完全平方式,右边是非负数的形式,再根据平方根的定义求解.注意开方后,等式的右边取“正、负”两种情况.
解:(1)移项,得x2=16.根据平方根的定义,得x=±4,即x1=4,x2=-4;
(2)移项,得3x2=27.两边同时除以3,得x2=9.根据平方根的定义,得x=±3,即x1=3,x2=-3;
(3)根据平方根的定义,得x-2=±3,即x-2=3或x-2=-3,即x1=5,x2=-1;
(4)根据平方根的定义,得2y-3=±4,即2y-3=4或2y-3=-4,即y1=,y2=-.
方法总结:直接开平方法是解一元二次方程的最基本的方法,也是学习配方法解一元二次方程的基础。它的理论依据是平方根的定义,它的可解类型有如下几种:①x2=a(a≥0);②(x+a)2=b(b≥0);③(ax+b)2=c(c≥0);④(ax+b)2=(cx+d)2(|a|≠|c|).
达标检测
一、选择题
1.一元二次方程x2-4=0的根为( )
A.x=2 B.x=-2 C.x1=2,x2=-2 D.x=4
2.已知一元二次方程可转化为两个一元一次方程,若其中一个一元一次方程是,则另一个一元一次方程是( )
A. B.
C. D.
3.关于x的一元二次方程(x-5)2=m-7,若能用直接开平方法解,则m的取值范围是( )
A.m>0 B.m≥7 C.m>7 D.任意实数
若2x2+3与2x2-4互为相反数,则x为( )
A. B.2 C.±2 D.±
5.关于x的一元二次方程(x-a)2=b,下列说法中正确的是( )
A.有两个解为x=± B.当b≥0时,有两个解为x=± +a
C.当b≥0时,有两个解为x=± -a D.当b≥0时,方程无实数根
二、填空题
6.方程4x2=9的解是________________.
7.方程(x+3)2-2=0的解为_________________.
8.若关于x的方程x2-m=0的一个根为,则另一个根为__________.
三、解答题
9.解方程:
(1)4=x2-1; (2)16x2-49=0;
(3)2(x-2)2=; (4)(2x-1)2=(x+1)2.
10.若2y=(x-2)2+1,且y的算术平方根是,求x+2y的值.
拓展与创新
阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,如=2×5-3×4=-2.如果=6,求x的值.
第1课时 直接开平方法
复习要点
1.学会用直接开平方法解形如(x+a)2=b(b≥0)的一元二次方程.
2、学会用直接开平方法解决简单实际问题.
知识框架
重难点阐释
【学习重点】熟练运用直接开平方法解一元二次方程
1.定义:一般地,对于形如x2=a (a≥0)的方程,根据平方根的定义可得
这种解一元二次方程的方法叫做直接开平方法.
2.直接开平方法解一元二次方程的基本步骤:移项(把常数项移到方程的右边)→开方(依据平方根的定义)→求解(解简单的一元一次方程)
【学习难点】
理解直接开平方法中的整体思想,形如(x+a)2=b(b≥0);(ax+b)2=c(c≥0);(ax+b)2=(cx+d)2(|a|≠|c|)的一元二次方程都可用直接开平方法来解,但要注意把括号里的部分看作一个整体,对其进行开平方,此外还需关注方程的右边必须是非负数,否则该一元二次方程无实数根,不可用直接开平方法.
典例突破
例:用直接开平方法解下列方程:
(1)x2-16=0; (2)3x2-27=0;
(3)(x-2)2=9; (4)(2y-3)2=16.
解析:用直接开平方法解方程时,要先将方程化成左边是含未知数的完全平方式,右边是非负数的形式,再根据平方根的定义求解.注意开方后,等式的右边取“正、负”两种情况.
解:(1)移项,得x2=16.根据平方根的定义,得x=±4,即x1=4,x2=-4;
(2)移项,得3x2=27.两边同时除以3,得x2=9.根据平方根的定义,得x=±3,即x1=3,x2=-3;
(3)根据平方根的定义,得x-2=±3,即x-2=3或x-2=-3,即x1=5,x2=-1;
(4)根据平方根的定义,得2y-3=±4,即2y-3=4或2y-3=-4,即y1=,y2=-.
方法总结:直接开平方法是解一元二次方程的最基本的方法,也是学习配方法解一元二次方程的基础。它的理论依据是平方根的定义,它的可解类型有如下几种:①x2=a(a≥0);②(x+a)2=b(b≥0);③(ax+b)2=c(c≥0);④(ax+b)2=(cx+d)2(|a|≠|c|).
达标检测
一、选择题
1.一元二次方程x2-4=0的根为( )
A.x=2 B.x=-2 C.x1=2,x2=-2 D.x=4
2.已知一元二次方程可转化为两个一元一次方程,若其中一个一元一次方程是,则另一个一元一次方程是( )
A. B.
C. D.
3.关于x的一元二次方程(x-5)2=m-7,若能用直接开平方法解,则m的取值范围是( )
A.m>0 B.m≥7 C.m>7 D.任意实数
若2x2+3与2x2-4互为相反数,则x为( )
A. B.2 C.±2 D.±
5.关于x的一元二次方程(x-a)2=b,下列说法中正确的是( )
A.有两个解为x=± B.当b≥0时,有两个解为x=± +a
C.当b≥0时,有两个解为x=± -a D.当b≥0时,方程无实数根
二、填空题
6.方程4x2=9的解是________________.
7.方程(x+3)2-2=0的解为_________________.
8.若关于x的方程x2-m=0的一个根为,则另一个根为__________.
三、解答题
9.解方程:
(1)4=x2-1; (2)16x2-49=0;
(3)2(x-2)2=; (4)(2x-1)2=(x+1)2.
10.若2y=(x-2)2+1,且y的算术平方根是,求x+2y的值.
拓展与创新
阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,如=2×5-3×4=-2.如果=6,求x的值.
