沪科版八年级数学下册17.2.2配方法复习学案(无答案)
文档属性
| 名称 | 沪科版八年级数学下册17.2.2配方法复习学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 33.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 09:42:32 | ||
图片预览


文档简介
17.2 一元二次方程的解法
第2课时 配方法
复习要点
1.理解配方法的思路,能熟练运用配方法解一元二次方程.
2. 通过复习配方法的概念,然后运用配方法解决一些具体题目.
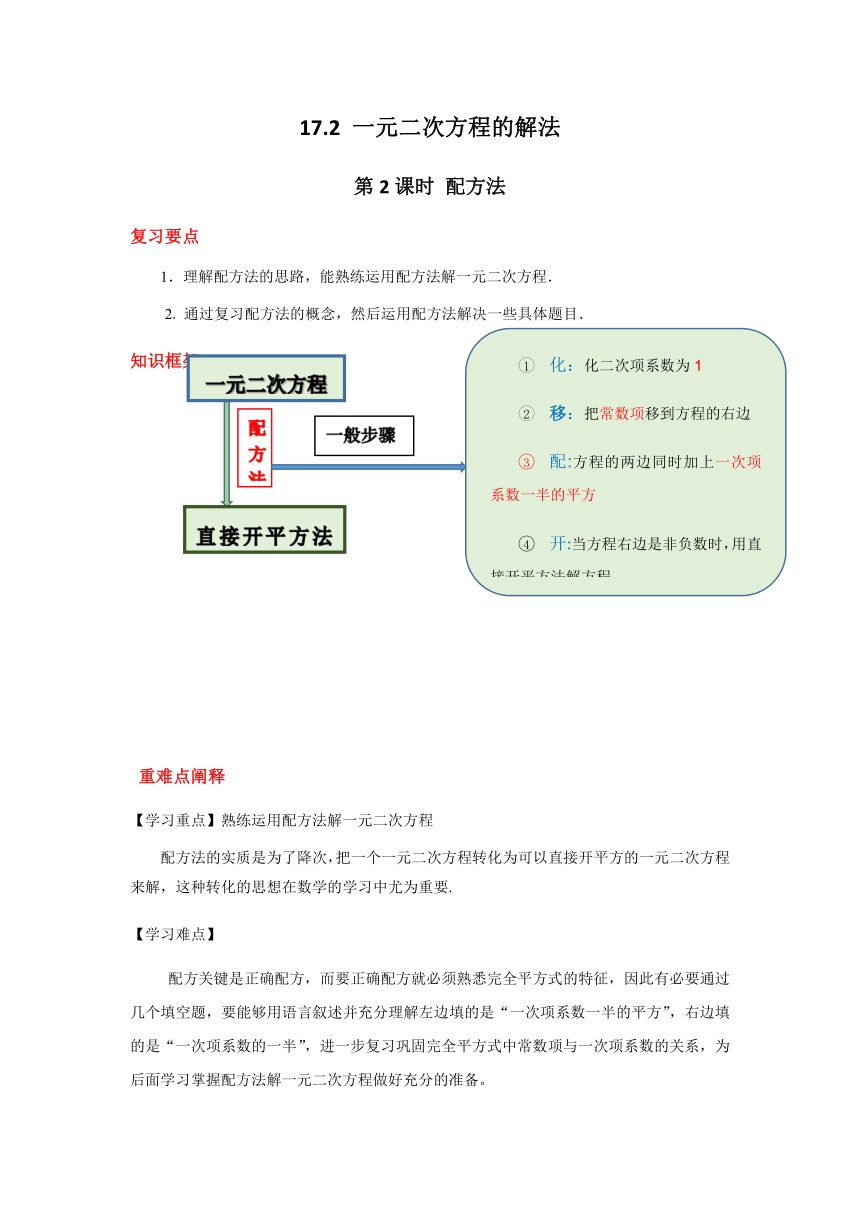
知识框架
重难点阐释
【学习重点】熟练运用配方法解一元二次方程
配方法的实质是为了降次,把一个一元二次方程转化为可以直接开平方的一元二次方程来解,这种转化的思想在数学的学习中尤为重要.
【学习难点】
配方关键是正确配方,而要正确配方就必须熟悉完全平方式的特征,因此有必要通过几个填空题,要能够用语言叙述并充分理解左边填的是“一次项系数一半的平方”,右边填的是“一次项系数的一半”,进一步复习巩固完全平方式中常数项与一次项系数的关系,为后面学习掌握配方法解一元二次方程做好充分的准备。
充分理解掌握用配方法解一元二次方程的基本思路及关键是将方程转化成(x+m)2=n(n≥0)的形式,并通过例题及练习总结出配方法的步骤。
典例突破
【类型一】 用配方法解一元二次方程
例1 用配方法解下列方程:
(1)x2-2x-35=0;
(2)3x2+8x-3=0.
解析:当二次项系数是1时,先把常数项移到右边,然后左、右两边同时加上一次项系数一半的平方,把左边配方成完全平方式,即为(x+m)2=n(n≥0)的形式,再用直接开平方法求解;当二次项系数不是1时,先将二次项系数化为1,再用配方法解方程.
解:(1)移项,得x2-2x=35.配方,得x2-2x+12=35+12,即(x-1)2=36.直接开平方,得x-1=±6.所以原方程的根是x1=7,x2=-5;
(2)方程两边同时除以3,得x2+x-1=0.移项,得x2+x=1.配方,得x2+x+()2=1+()2,即(x+)2=()2.直接开平方,得x+=±.所以原方程的根是x1=,x2=-3.
方法总结:运用配方法解一元二次方程的关键是先把一元二次方程转化为二次项系数为1的一元二次方程,然后在方程两边同时添加常数项,使其等于一次项系数一半的平方.
【类型二】 利用配方法求代数式的值
例2 已知a2-3a+b2-+=0,求a-4的值.
解析:观察方程可以知道,原方程可以用配方法转化为两个数的平方和等于0的形式,得到这两个数都为0,从而可求出a,b的值,再代入代数式计算即可.
解:原等式可以写成:(a-)2+(b-)2=0.
∴a-=0,b-=0,解得a=,b=.
∴a-4=-4×=-.
方法总结:这类题目主要是配方法和平方的非负性的综合应用,通过配方把等式转化为两个数的平方和等于0的形式是解题的关键.
达标检测
一.选择题
1.要用配方法解一元二次方程x2﹣4x﹣3=0,那么下列变形的结果中正确的是( )
A.x2﹣4x+4=9 B.x2﹣4x+4=7 C.x2﹣4x+16=19 D.x2﹣4x+2=5
2.要使方程x2﹣x=左边能成完全平方式应该在方程的两边都加上( )
A.(﹣)2 B.(﹣)2 C.()2 D.()2
3.把方程左边配成一个完全平方式后,所得方程是( )
A. B. C. D.
4.将一元二次方程x2﹣4x﹣6=0化成(x﹣a)2=b的形式,则b等于( )
A.4 B.6 C.8 D.10
5.已知等腰三角形的一边长为8,另一边长为方程x2﹣6x+9=0的根,则该等腰三角形的周长为( )
A.14 B.19 C.14或19 D.不能确定
填空题
6.用配方法解一元二次方程﹣3x2+4x+1=0的第一步是把方程的两边同时除以 .
7.用配方法解一元二次方程x2+2x﹣3=0 时,方程变形正确的是 (填序号)
①(x﹣1)2=2 ②(x+1)2=4 ③(x﹣1)2=1④(x+1)2=7.
若a为实数,则代数式a2+4a﹣6的最小值为 .
三.解答题
9.用配方法下列解方程:
(1)x2+6x+8=0; (2) x2=6x+16;
(3)2x2+3=7x; (4)(2x﹣1)(x+3)=4.
10.小明在解方程x2﹣2x﹣1=0时出现了错误,其解答过程如下:
x2﹣2x=﹣1 (第一步)
x2﹣2x+1=﹣1+1 (第二步)
(x﹣1)2=0 (第三步)
x1=x2=1 (第四步)
(1)小明解答过程是从第 步开始出错的,其错误原因是 ;
(2)请写出此题正确的解答过程.
拓展与创新
用配方法解关于x的一元二次方程:x2﹣2ax-8a2 =0
第2课时 配方法
复习要点
1.理解配方法的思路,能熟练运用配方法解一元二次方程.
2. 通过复习配方法的概念,然后运用配方法解决一些具体题目.
知识框架
重难点阐释
【学习重点】熟练运用配方法解一元二次方程
配方法的实质是为了降次,把一个一元二次方程转化为可以直接开平方的一元二次方程来解,这种转化的思想在数学的学习中尤为重要.
【学习难点】
配方关键是正确配方,而要正确配方就必须熟悉完全平方式的特征,因此有必要通过几个填空题,要能够用语言叙述并充分理解左边填的是“一次项系数一半的平方”,右边填的是“一次项系数的一半”,进一步复习巩固完全平方式中常数项与一次项系数的关系,为后面学习掌握配方法解一元二次方程做好充分的准备。
充分理解掌握用配方法解一元二次方程的基本思路及关键是将方程转化成(x+m)2=n(n≥0)的形式,并通过例题及练习总结出配方法的步骤。
典例突破
【类型一】 用配方法解一元二次方程
例1 用配方法解下列方程:
(1)x2-2x-35=0;
(2)3x2+8x-3=0.
解析:当二次项系数是1时,先把常数项移到右边,然后左、右两边同时加上一次项系数一半的平方,把左边配方成完全平方式,即为(x+m)2=n(n≥0)的形式,再用直接开平方法求解;当二次项系数不是1时,先将二次项系数化为1,再用配方法解方程.
解:(1)移项,得x2-2x=35.配方,得x2-2x+12=35+12,即(x-1)2=36.直接开平方,得x-1=±6.所以原方程的根是x1=7,x2=-5;
(2)方程两边同时除以3,得x2+x-1=0.移项,得x2+x=1.配方,得x2+x+()2=1+()2,即(x+)2=()2.直接开平方,得x+=±.所以原方程的根是x1=,x2=-3.
方法总结:运用配方法解一元二次方程的关键是先把一元二次方程转化为二次项系数为1的一元二次方程,然后在方程两边同时添加常数项,使其等于一次项系数一半的平方.
【类型二】 利用配方法求代数式的值
例2 已知a2-3a+b2-+=0,求a-4的值.
解析:观察方程可以知道,原方程可以用配方法转化为两个数的平方和等于0的形式,得到这两个数都为0,从而可求出a,b的值,再代入代数式计算即可.
解:原等式可以写成:(a-)2+(b-)2=0.
∴a-=0,b-=0,解得a=,b=.
∴a-4=-4×=-.
方法总结:这类题目主要是配方法和平方的非负性的综合应用,通过配方把等式转化为两个数的平方和等于0的形式是解题的关键.
达标检测
一.选择题
1.要用配方法解一元二次方程x2﹣4x﹣3=0,那么下列变形的结果中正确的是( )
A.x2﹣4x+4=9 B.x2﹣4x+4=7 C.x2﹣4x+16=19 D.x2﹣4x+2=5
2.要使方程x2﹣x=左边能成完全平方式应该在方程的两边都加上( )
A.(﹣)2 B.(﹣)2 C.()2 D.()2
3.把方程左边配成一个完全平方式后,所得方程是( )
A. B. C. D.
4.将一元二次方程x2﹣4x﹣6=0化成(x﹣a)2=b的形式,则b等于( )
A.4 B.6 C.8 D.10
5.已知等腰三角形的一边长为8,另一边长为方程x2﹣6x+9=0的根,则该等腰三角形的周长为( )
A.14 B.19 C.14或19 D.不能确定
填空题
6.用配方法解一元二次方程﹣3x2+4x+1=0的第一步是把方程的两边同时除以 .
7.用配方法解一元二次方程x2+2x﹣3=0 时,方程变形正确的是 (填序号)
①(x﹣1)2=2 ②(x+1)2=4 ③(x﹣1)2=1④(x+1)2=7.
若a为实数,则代数式a2+4a﹣6的最小值为 .
三.解答题
9.用配方法下列解方程:
(1)x2+6x+8=0; (2) x2=6x+16;
(3)2x2+3=7x; (4)(2x﹣1)(x+3)=4.
10.小明在解方程x2﹣2x﹣1=0时出现了错误,其解答过程如下:
x2﹣2x=﹣1 (第一步)
x2﹣2x+1=﹣1+1 (第二步)
(x﹣1)2=0 (第三步)
x1=x2=1 (第四步)
(1)小明解答过程是从第 步开始出错的,其错误原因是 ;
(2)请写出此题正确的解答过程.
拓展与创新
用配方法解关于x的一元二次方程:x2﹣2ax-8a2 =0
