沪科版版八年级数学下册17.1 一元二次方程 复习学案(无答案)
文档属性
| 名称 | 沪科版版八年级数学下册17.1 一元二次方程 复习学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 09:49:13 | ||
图片预览


文档简介
17.1 一元二次方程
复习要点
1、了解一元二次方程的意义,并能根据实际意义建立方程.
2、掌握一元二次方程的一般形式.
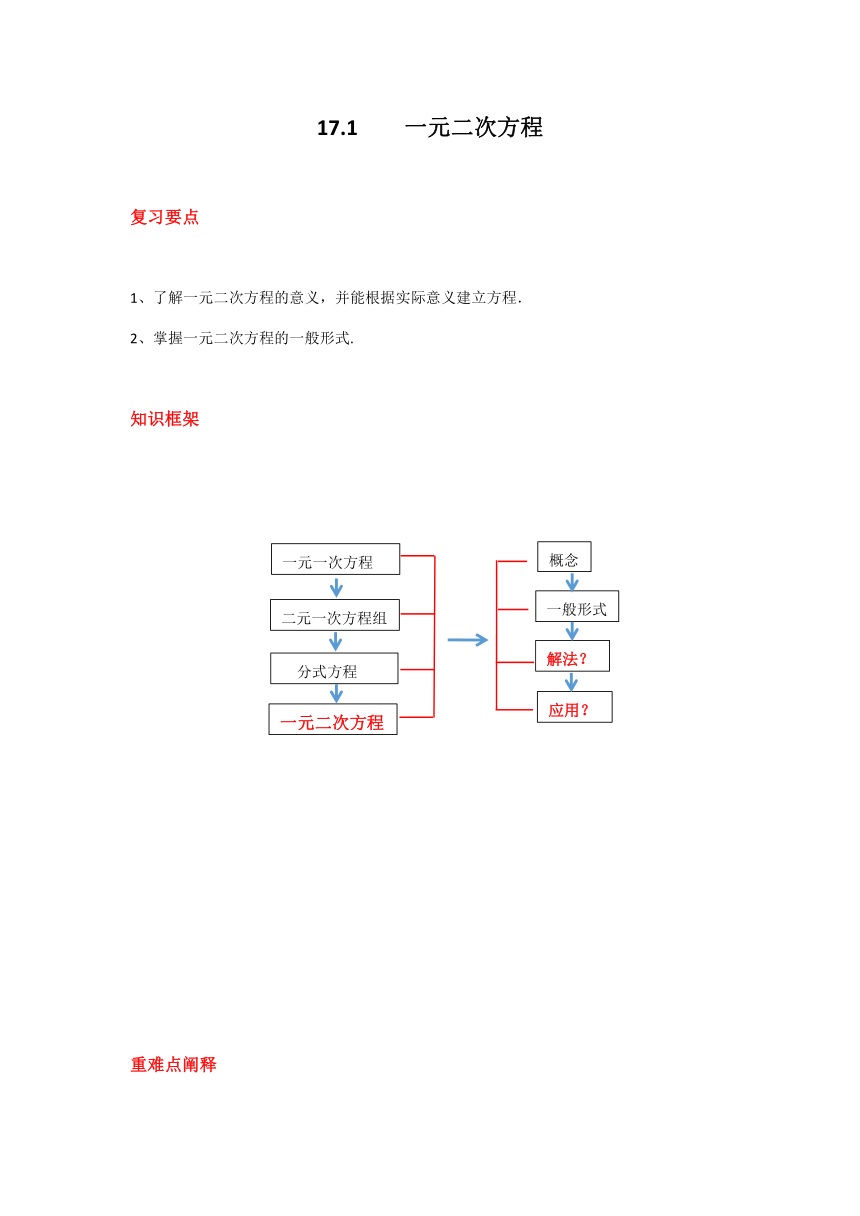
知识框架
重难点阐释
【学习重点】
一元二次方程的概念及其一般形式.
【学习难点】
确定一元二次方程的各项及各项系数.
对一元二次方程概念的理解(三个关键条件):
①一个未知数;②未知数的最高次数是2;③方程两边都是整式.
一元二次方程的一般形式:(a,b,c为常数,且a≠0)
其中:①在“(a,b,c为常数)”中,“a≠0”是方程为一元二次方程的充分且必要条件
即:a≠0 是一元二次方程
②和c分别是此一元二次方程的二次项、一次项和常数项,
a、b分别是二次项系数、一次项系数.
③在一元二次方程的一般形式下,方可确定方程的各项及各项系数。
1、当a为何值时,方程是关于x的一元二次方程?
切入点:一元二次方程的概念(从所满足的条件入手)
2、写出方程的二次项系数、一次项系数及常数项。
切入点:先化为一元二次方程的“一般形式”
典例突破
【例1】下列关于x的方程中,属于一元二次方程的是__________.
①;②;③;
④;⑤;⑥
【解析】判断一个方程是否为一元二次方程的方法:首先看方程是否为整式方程;
其次,通过变形后,若同时满足:只含有一个未知数,且未知数的最高次
数是2,则是一元二次方程,否则,不是。
【答案】②⑤
【例2】把方程化为一般形式,并写出它的二次项系数、一次项系
数及常数项。
【解析】一元二次方程的一般形式为,其中a≠0,a、b、c分别
是二次项系数、一次项系数、常数项。
【答案】去括号,得:,整理,得:,所以,
二次项系数是3,一次项系数是-5,常数项是-12.
达标检测
一、选择:
1.下列关于x的方程中,是一元二次方程的是( )
A. B.
C. D.
2.下列关于x的一元二次方程中,是一般形式的是( )
A. B.
C. D.
3. 关于x的一元二次方程,它的二次项系数,一次项系数及常数项是( )
A.-3,1,1 B.3,-1,-1 C.-3,-1,-1 D.3,-1,1
二、填空:
1. 已知,则分别以a、b、c为二次项系数、一次项
系数、常数项的一元二次方程是______________________.
2. 已知是关于x的一元二次方程,则此方程的常数项是___________.
3. 若m是方程的解,则=__________.
三、解答:
已知a、b、c分别的关于x的一元二次方程的二次项系数、一次项系数、常数项,请写出分别以c、b、a为二次项系数、一次项系数、常数项的一元二次方程(未知数为y)。
拓展与创新
已知关于x的方程
当m为何值时,此方程为一元一次方程?求出此时方程的解;
当m为何值时,此方程为一元二次方程?
复习要点
1、了解一元二次方程的意义,并能根据实际意义建立方程.
2、掌握一元二次方程的一般形式.
知识框架
重难点阐释
【学习重点】
一元二次方程的概念及其一般形式.
【学习难点】
确定一元二次方程的各项及各项系数.
对一元二次方程概念的理解(三个关键条件):
①一个未知数;②未知数的最高次数是2;③方程两边都是整式.
一元二次方程的一般形式:(a,b,c为常数,且a≠0)
其中:①在“(a,b,c为常数)”中,“a≠0”是方程为一元二次方程的充分且必要条件
即:a≠0 是一元二次方程
②和c分别是此一元二次方程的二次项、一次项和常数项,
a、b分别是二次项系数、一次项系数.
③在一元二次方程的一般形式下,方可确定方程的各项及各项系数。
1、当a为何值时,方程是关于x的一元二次方程?
切入点:一元二次方程的概念(从所满足的条件入手)
2、写出方程的二次项系数、一次项系数及常数项。
切入点:先化为一元二次方程的“一般形式”
典例突破
【例1】下列关于x的方程中,属于一元二次方程的是__________.
①;②;③;
④;⑤;⑥
【解析】判断一个方程是否为一元二次方程的方法:首先看方程是否为整式方程;
其次,通过变形后,若同时满足:只含有一个未知数,且未知数的最高次
数是2,则是一元二次方程,否则,不是。
【答案】②⑤
【例2】把方程化为一般形式,并写出它的二次项系数、一次项系
数及常数项。
【解析】一元二次方程的一般形式为,其中a≠0,a、b、c分别
是二次项系数、一次项系数、常数项。
【答案】去括号,得:,整理,得:,所以,
二次项系数是3,一次项系数是-5,常数项是-12.
达标检测
一、选择:
1.下列关于x的方程中,是一元二次方程的是( )
A. B.
C. D.
2.下列关于x的一元二次方程中,是一般形式的是( )
A. B.
C. D.
3. 关于x的一元二次方程,它的二次项系数,一次项系数及常数项是( )
A.-3,1,1 B.3,-1,-1 C.-3,-1,-1 D.3,-1,1
二、填空:
1. 已知,则分别以a、b、c为二次项系数、一次项
系数、常数项的一元二次方程是______________________.
2. 已知是关于x的一元二次方程,则此方程的常数项是___________.
3. 若m是方程的解,则=__________.
三、解答:
已知a、b、c分别的关于x的一元二次方程的二次项系数、一次项系数、常数项,请写出分别以c、b、a为二次项系数、一次项系数、常数项的一元二次方程(未知数为y)。
拓展与创新
已知关于x的方程
当m为何值时,此方程为一元一次方程?求出此时方程的解;
当m为何值时,此方程为一元二次方程?
