人教版高中数学必修三2.3.2两个变量的线性相关(共38张PPT)
文档属性
| 名称 | 人教版高中数学必修三2.3.2两个变量的线性相关(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 00:00:00 | ||
图片预览



文档简介
(共38张PPT)
《普通高中课程标准实验教科书·数学(人教A版)》必修3第二章
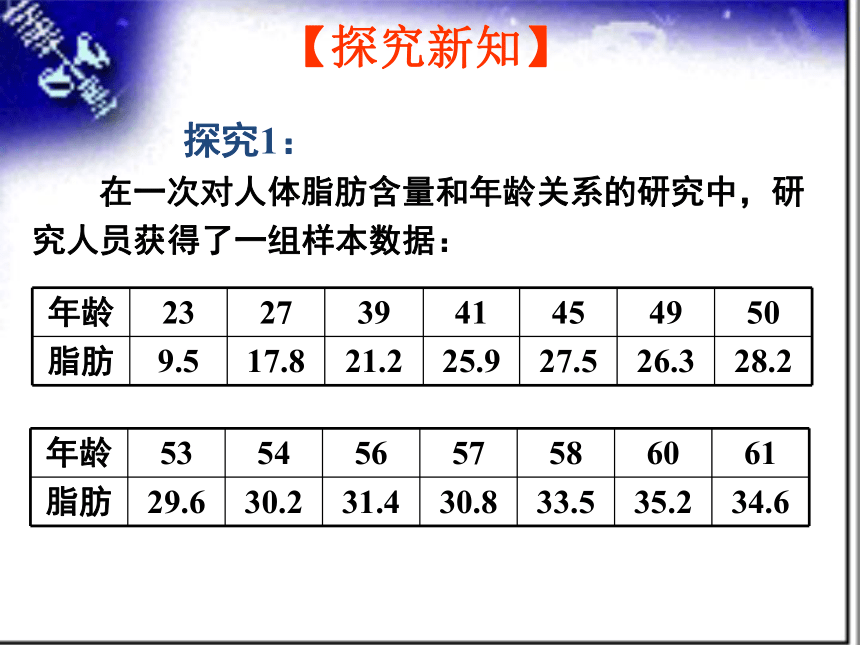
探究1:
在一次对人体脂肪含量和年龄关系的研究中,研
究人员获得了一组样本数据:
【探究新知】
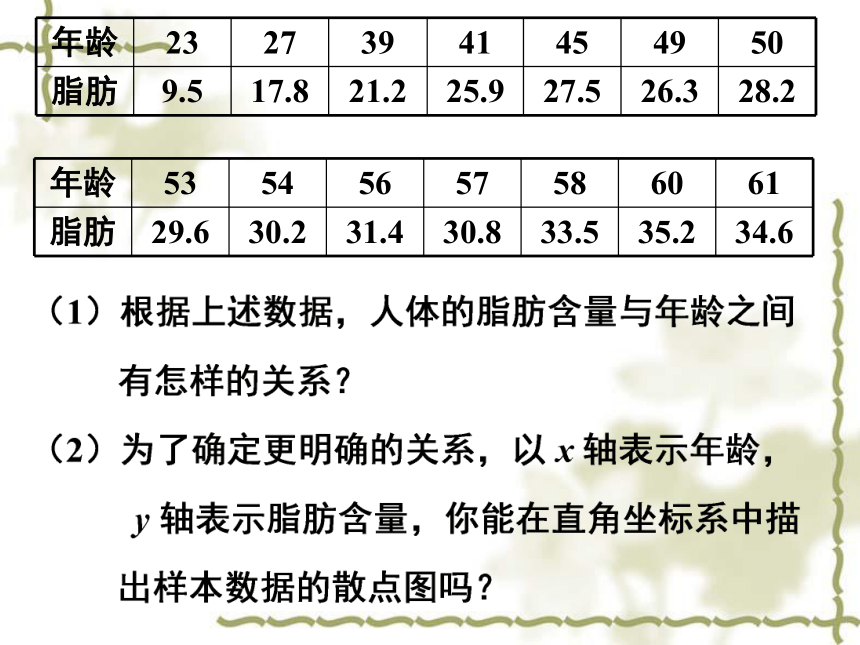
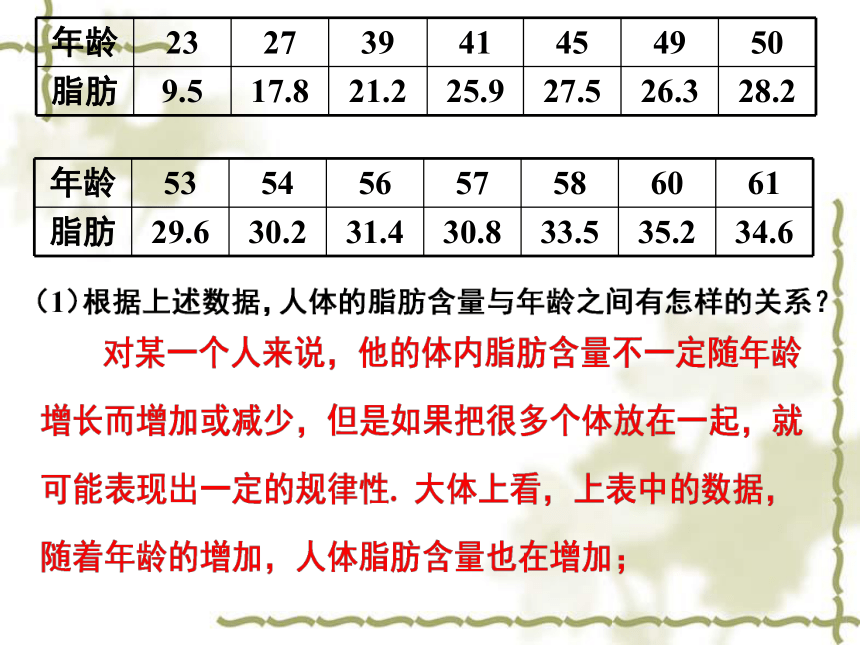
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
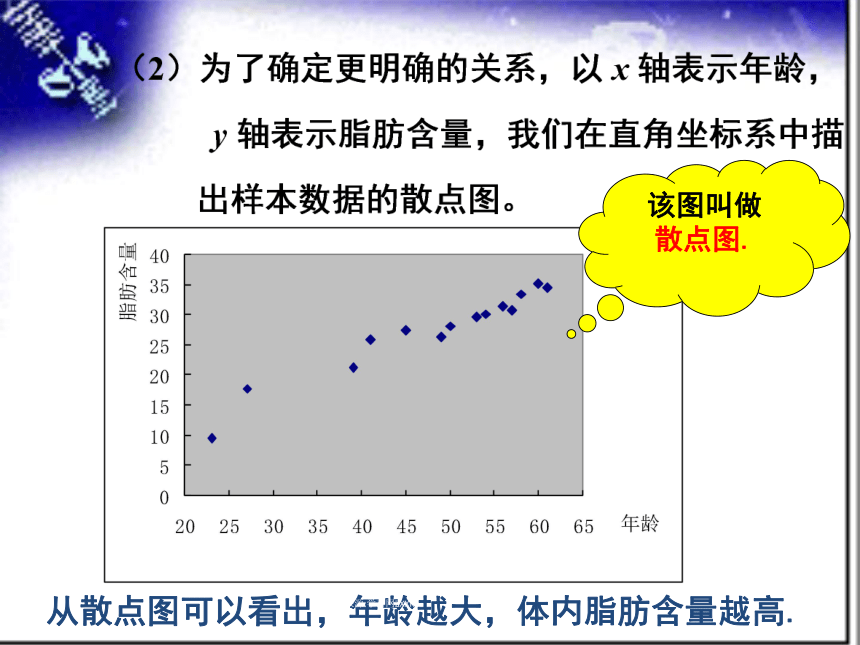
该图叫做
散点图.
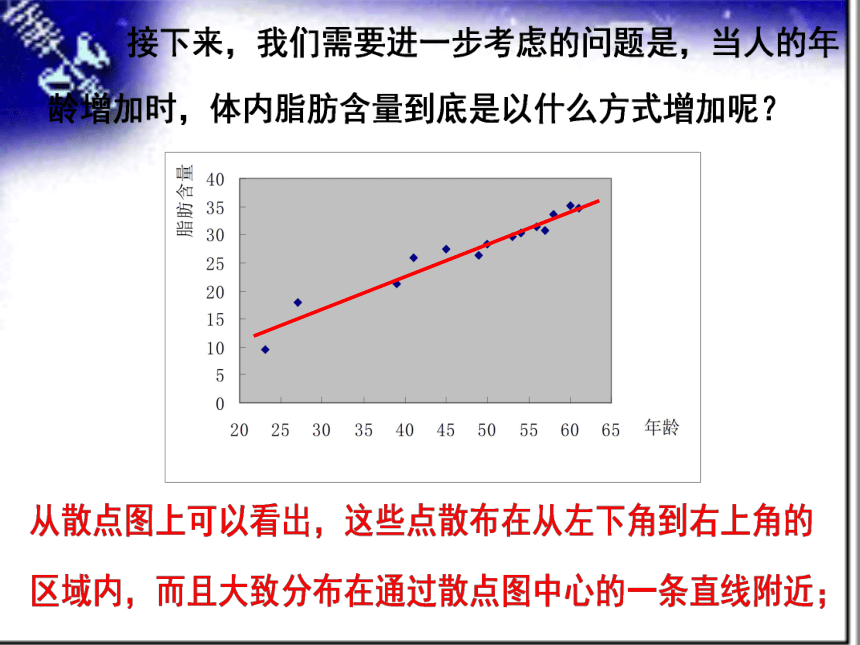
从散点图可以看出,年龄越大,体内脂肪含量越高.
[来源:学科网ZXXK]
(1)如果所有的样本点都落在某一函数曲线上,变量
之间具有函数关系;
(2)如果所有的样本点都落在某一曲线附近,变量之
间就有相关关系;
(3)如果所有的样本点都落在某一直线附近,变量之
间就有线性相关关系;
只有散点图中的点呈条状集中在某一直线周围,
才可以用回归直线来描述两个变量之间的关系. 如何具体求出这条直线方程呢?
【明确概念】
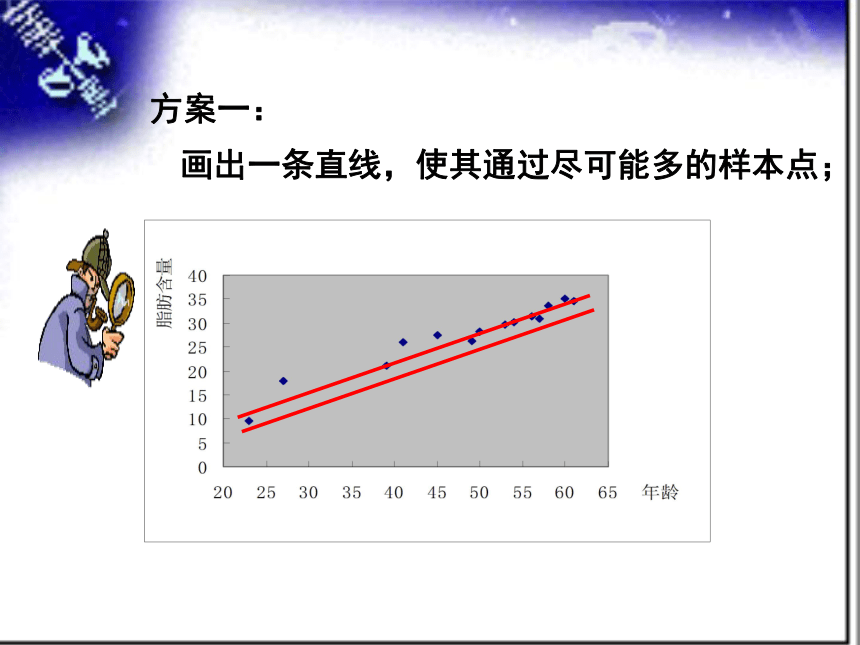
方案一:
画出一条直线,使其通过尽可能多的样本点;
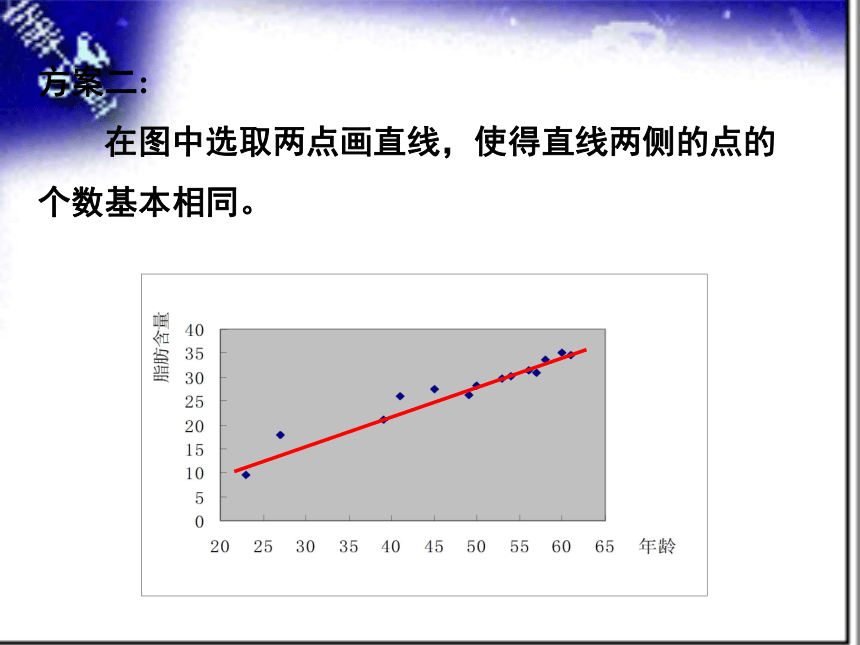
方案二:
在图中选取两点画直线,使得直线两侧的点的
个数基本相同。
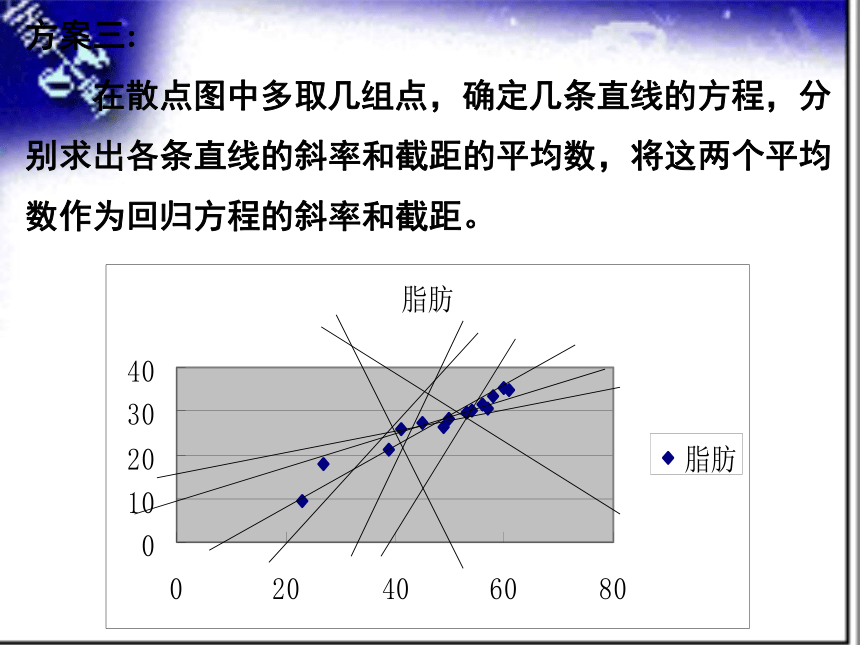
方案三:
在散点图中多取几组点,确定几条直线的方程,分
别求出各条直线的斜率和截距的平均数,将这两个平均
数作为回归方程的斜率和截距。
假设我们已经得到两个具有线性相关关系的样本
的一组数据:(x1,y1),(x2,y2),…,(xn,yn),
且所求回归直线方程是: ,其中 是
待定系数.
(x1,y1)
(x2,y2)
(xn,yn)
(x3,y3)
{
当自变量x取xi(i=1,2,…,n)时可以得到回归直
线上的点的纵坐标为:
它与样本数据yi的偏差是:
表示出各点到直线的远近
运算不方便
避免相互抵消
各点与直线
的整体偏差
这种通过求:
的最小值而得到回归直线的方法,即求样本数据的点到
回归直线的距离的平方和最小的方法叫做最小二乘法.
回归方程的系数公式:
从而求出线性回归方程:
.
归纳:
分析两个变量的线性相关关系的步骤:
.
归纳:
求回归方程 的步骤:
【典例剖析】
?
?
?
?
?
?
?
?
?
?
《普通高中课程标准实验教科书·数学(人教A版)》必修3第二章
【典例剖析】
(2)由题意得:
回归方程为:
(3)由回归方程预测,
即记忆力为9的同学的判断力约为4.
利用计算机,可以方便的求出回归方程.
.
归纳:
分析两个变量的线性相关关系的步骤:
【知识归纳】
.
归纳:
求回归方程 的步骤(最小二乘法):
【知识归纳】
2、某数学老师身高176cm,他爷爷、父亲和儿子的
身高分别是173cm、170cm、和182cm. 因儿子的
身高与父亲的身高有关,该老师用线性回归分析
的方法预测他孙子的身高为_________ cm.
185
解析:由题意得父亲和儿子的身高组成了3个坐标:
(173,170), (170,176),(176,182),
1、本节知识容量较大,思维量较高,教师利用实例
分析了散点图的分布规律,推导出了线性回归直
线的方程的求法,运用实例分析比较,帮助同学
们养成良好的学习态度,培养勤奋刻苦的精神;
2、把课堂还给学生,让学生多动手、动脑,对学生
有难度的知识老师给予有梯度的提示,引导学生
主动探究与思考,让学生真正参与到课堂中来;
3、教师可让学有余力的学生课下继续探讨,达到灵
活运用.
【教学反思】
回归方程为:
解:
65.5
【典例剖析】
(1)散点图:
(2)正相关、负相关:
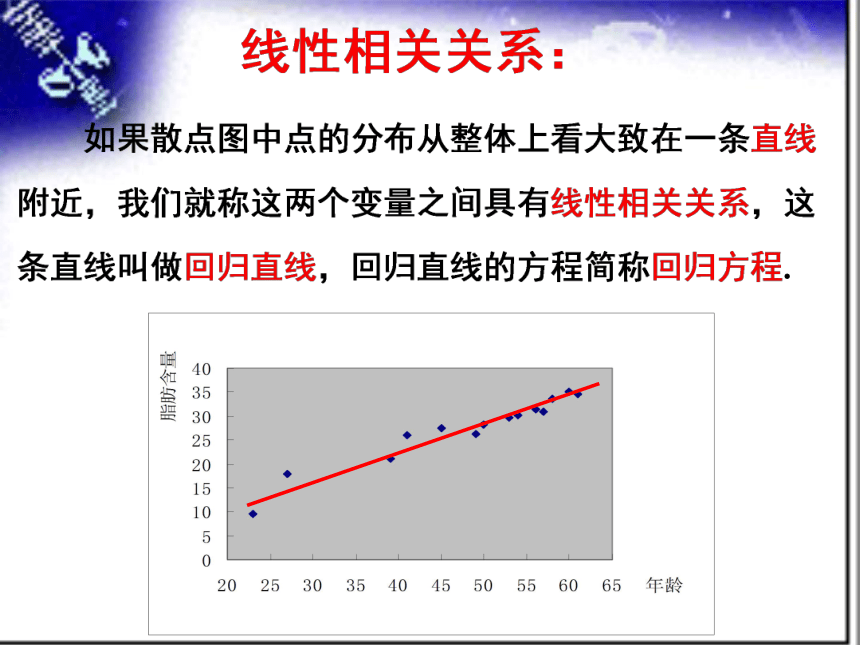
(3)线性相关关系:
(4)回归方程的系数公式:
【知识归纳】
1、知识:
(1)最小二乘法:
(2)转化与化归;
数形结合;
2、思想方法:
【变式训练】
解:(1)散点图如图示:
(2)由题意得:
回归方程为:
(3)由回归方程预测,现在生产100吨产品消耗煤数
量为 :
故耗能减少了90-70.35=19.65(吨)
《普通高中课程标准实验教科书·数学(人教A版)》必修3第二章
探究1:
在一次对人体脂肪含量和年龄关系的研究中,研
究人员获得了一组样本数据:
【探究新知】
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
该图叫做
散点图.
从散点图可以看出,年龄越大,体内脂肪含量越高.
[来源:学科网ZXXK]
(1)如果所有的样本点都落在某一函数曲线上,变量
之间具有函数关系;
(2)如果所有的样本点都落在某一曲线附近,变量之
间就有相关关系;
(3)如果所有的样本点都落在某一直线附近,变量之
间就有线性相关关系;
只有散点图中的点呈条状集中在某一直线周围,
才可以用回归直线来描述两个变量之间的关系. 如何具体求出这条直线方程呢?
【明确概念】
方案一:
画出一条直线,使其通过尽可能多的样本点;
方案二:
在图中选取两点画直线,使得直线两侧的点的
个数基本相同。
方案三:
在散点图中多取几组点,确定几条直线的方程,分
别求出各条直线的斜率和截距的平均数,将这两个平均
数作为回归方程的斜率和截距。
假设我们已经得到两个具有线性相关关系的样本
的一组数据:(x1,y1),(x2,y2),…,(xn,yn),
且所求回归直线方程是: ,其中 是
待定系数.
(x1,y1)
(x2,y2)
(xn,yn)
(x3,y3)
{
当自变量x取xi(i=1,2,…,n)时可以得到回归直
线上的点的纵坐标为:
它与样本数据yi的偏差是:
表示出各点到直线的远近
运算不方便
避免相互抵消
各点与直线
的整体偏差
这种通过求:
的最小值而得到回归直线的方法,即求样本数据的点到
回归直线的距离的平方和最小的方法叫做最小二乘法.
回归方程的系数公式:
从而求出线性回归方程:
.
归纳:
分析两个变量的线性相关关系的步骤:
.
归纳:
求回归方程 的步骤:
【典例剖析】
?
?
?
?
?
?
?
?
?
?
《普通高中课程标准实验教科书·数学(人教A版)》必修3第二章
【典例剖析】
(2)由题意得:
回归方程为:
(3)由回归方程预测,
即记忆力为9的同学的判断力约为4.
利用计算机,可以方便的求出回归方程.
.
归纳:
分析两个变量的线性相关关系的步骤:
【知识归纳】
.
归纳:
求回归方程 的步骤(最小二乘法):
【知识归纳】
2、某数学老师身高176cm,他爷爷、父亲和儿子的
身高分别是173cm、170cm、和182cm. 因儿子的
身高与父亲的身高有关,该老师用线性回归分析
的方法预测他孙子的身高为_________ cm.
185
解析:由题意得父亲和儿子的身高组成了3个坐标:
(173,170), (170,176),(176,182),
1、本节知识容量较大,思维量较高,教师利用实例
分析了散点图的分布规律,推导出了线性回归直
线的方程的求法,运用实例分析比较,帮助同学
们养成良好的学习态度,培养勤奋刻苦的精神;
2、把课堂还给学生,让学生多动手、动脑,对学生
有难度的知识老师给予有梯度的提示,引导学生
主动探究与思考,让学生真正参与到课堂中来;
3、教师可让学有余力的学生课下继续探讨,达到灵
活运用.
【教学反思】
回归方程为:
解:
65.5
【典例剖析】
(1)散点图:
(2)正相关、负相关:
(3)线性相关关系:
(4)回归方程的系数公式:
【知识归纳】
1、知识:
(1)最小二乘法:
(2)转化与化归;
数形结合;
2、思想方法:
【变式训练】
解:(1)散点图如图示:
(2)由题意得:
回归方程为:
(3)由回归方程预测,现在生产100吨产品消耗煤数
量为 :
故耗能减少了90-70.35=19.65(吨)
