北京版七年级下册数学课件:第五章 二元一次方程组复习 (共39张PPT)
文档属性
| 名称 | 北京版七年级下册数学课件:第五章 二元一次方程组复习 (共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 21:44:31 | ||
图片预览











文档简介
(共34张PPT)
初一年级 数学
二元一次方程组复习
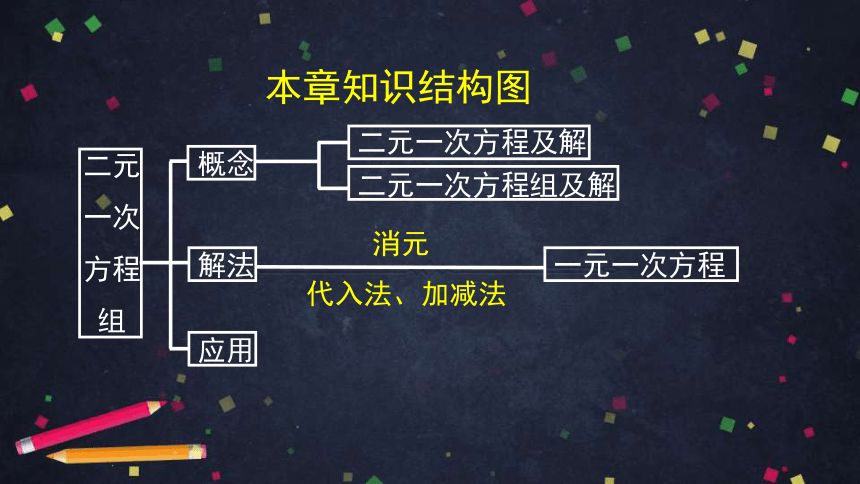
本章知识结构图
二元
一次
方程
组
概念
解法
应用
一元一次方程
二元一次方程及解
二元一次方程组及解
消元
代入法、加减法
本章知识回顾
1.二元一次方程及其解的概念
(1)二元一次方程:
含有两个未知数,并且含有未知数的项的次数都是“1”的方程,叫二元一次方程.
标准形式:ax+by=c(a≠0,b≠0).
(一)、概念
特别要注意a≠0,b≠0.
本章知识回顾
1.二元一次方程及其解的概念
(2)二元一次方程的解:
使二元一次方程左右两边的值相等的一对未知数的值,
叫做这个二元一次方程的一个解.
(一)、概念
一般地,一个二元一次方程有无数个解.
本章知识回顾
2.二元一次方程组及其解的概念
(1)二元一次方程组:
一般地,含有相同未知数的两个二元一次方程合在一
起,就组成了一个二元一次方程组.
也就是这个方程组一共含两个未知数,含未知数的项
的次数是 “1”.
(一)、概念
本章知识回顾
2.二元一次方程组及其解的概念
(2)二元一次方程组的解:
使二元一次方程组中的两个方程左右两边的值都相等
的两个未知数的值(即两个方程的公共解),叫做二元
一次方程组的解.
(一)、概念
本章知识回顾
解二元一次方程组的基本思想是“消元”.
消元的方法有两种:代入法、加减法.
(二)、解法
每个方程组都可以用这两种方法求解,在解题时要根据方程组中未知数的系数特点,确定用哪一种方法比较简便.
本章知识回顾
当方程组中某一未知数的系数是“1”或“-1”时用代入法比较简单.
(二)、解法
一定要仔细观察方程组的特点,有时方程组中的某一部分可以看做一个“整体”,可以用“整体思想”代入,从而达到消元的目的.
本章知识回顾
(二)、解法
当方程组中同一未知数的系数相同或互为相反数时用加减法求解简单.当同一未知数系数绝对值不同,可以求系数绝对值的最小公倍数,将该未知数系数绝对值化为最小公倍数,再用加减法求解.
当方程组比较复杂时通常先进行整理,观察特点,确定求解方法,再求解.
本章知识回顾
基本思想:实际问题转化为数学问题,得到数学问题的解,
检验是否符合实际问题,从而得到实际问题的答案.
(三)、应用
关键:确定等量关系.
步骤:审、设、列、解、验、答.
典型例题
例1. 如果方程 是关于x,y的二元一次方程,则k的值是 .
分析:由未知数x的次数是“1”,得到|k|-1=1,k=±2,这是最容易出现的错误.
本题应该满足的条件是:
二元一次方程的标准形式是ax+by=c (其中a≠0,b≠0).当k-2=0时方程变成了一元一次方程.
典型例题
分析:根据二元一次方程解的定义,得到2a+2=6.
A
例2.已知 是二元一次方程ax+2y=6的一个解,那
么a的值为( ).
A.2 B.-2 C.4 D. -4
典型例题
例3.下列方程组:① ②
③ 其中是二元一次方程组的是( ).
A.①② B.②③ C.①③ D.③
分析:①含有三个未知数, ②中的第一个方程不是整式方程.
D
例4.下列x,y的各对数值中,是方程组 的解的是( ).
典型例题
A.
B.
C.
D.
分析:可以依据二元一次方程组解的定义,也可以用解方程组的方法求解问题,随着所学知识的增多,解决同一问题的方法也会增多,要学会发展地解决问题.
C
典型例题
例5.解方程组:
分析:方程组中的第一个方程有分母,第二个方程中有括
号,先把两个方程进行整理,得
用加减法或代入法求解.
典型例题
例5.解方程组:
解:整理,得
①
②
②-①,得
把y=2 代入②,得
∴方程组的解是
方法一:减法消元
y=2.
x=2.
典型例题
例5.解方程组:
解:整理,得
①
②
方法二:代入消元法
把③代入① ,得
由② ,得
③
解得
把 代入③ ,得
∴方程组的解是
典型例题
例5.解方程组:
①
②
∴方程组的解是
把x=2代入② ,得
y=2.
解:把②代入① ,得
方法三:两个方程中都有y+1,
可以整体代入消元.
典型例题
例5.解方程组:
小结:比较三种解法,观察点不同,切入点不同,选择的方法就会不同,在解题中要根据方程组特点选择恰当方法进行求解.
典型例题
例6. 当x=-3和x=2时,代数式kx+b的值分别是-4和11.
(1)求k,b的值.
(2)求x为何值时,代数式kx+b的值是0.
分析:x=-3和x=2时的值分别是-4和11代入可得关于k,b的方程组,求解即得k,b的值,代数式确定.由代数式的值是0,可得关于x的一元一次方程.
典型例题
例6. 当x=-3和x=2时,代数式kx+b的值分别是-4和11.
(1)求k,b的值.
(2)求x为何值时,代数式kx+b的值是0.
解得
∴k,b的值分别为3,5.
(2)由(1)得代数式为3x+5,根据题意,得3x+5=0.
∴ 时,代数式3x+5的值为0.
解:(1)根据题意,得
典型例题
甲同学:先解关于x,y 的方程组 ,再求k的值.
乙同学:先将方程组中的两个方程相加, 再求k的值.
丙同学:先解方程组 再求k的值.
你最欣赏哪种思路?根据你选的思路解答此题,再对选择的思路进行简要评价.
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
∵ x+y=2,
∴
解得
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
解:依照甲同学思路,解 得
典型例题
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
∵ x+y=2,
∴ 5x+5y=10.即7k+4=10.解得
①
②
解:依照乙同学思路,方程组
①+②,得
例7. 已知有理数x,y满足x+y=2
求k的值.
典型例题
∵ 3x+2y=7k-2,
∴ 7k-2=4.解得
解:依照丙同学思路,解方程组
解得
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
小结:甲的方法是解决这类问题的通法,而后两种方法是根据本题特点确定的方法.很显然乙、丙的方法计算量小,要明显优于甲同学的方法.丙和甲解法相同之处是解方程组,丙比甲巧的是重新组合方程组,解起来简单.乙的方法最巧.因此在解题中要学会处理通法与特殊方法之间的关系,选用最简单的方法.
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
小结:已知关于x,y的方程组满足 又出现与
x+y(或x-y)相关的条件,就可以直接①+②(或①-②).
①
②
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
例8. 每年的3月12日是植树节.某校七年级有183名学生参加植树节活动,在活动中男生平均每人挖3个树坑,女生平均每人种6棵树,这样恰好使挖好的树坑都能种上树.该年级参加植树的男、女生各有多少人?
分析:审题明确已知量、未知量,分析数量关系,确定等量关系.
等量关系: 男生人数+女生人数=183;
男生挖树坑总数=女生种树总数.
典型例题
等量关系: 男生人数+女生人数=183;
男生挖树坑总数=女生种树总数.
解:设七年级参加植树的男生x人,女生y人.根据题意,得
解方程组,得
答:七年级参加植树的男生122人,女生61人.
课堂小结
本章内容:
四个概念;
两种方法(代入法、加减法);
四种思想(消元、转化、化归、建模);
一个意识(应用意识).
理解概念、掌握方法、体会思想,提升意识.
作业
1.如果方程 是关于x,y的二元一次方程,则m的值是 .
2.请判断下面的两对数是不是方程2x-y=5的解.
作业
3.解下列方程组:
4.一个正方体,其中有一对相对的面上的数字之和是29,差是7,这两个数各是多少?
5. 已知关于x,y的二元一次方程组 和
的解相同,试求m,n的取值范围.
作业
数学的复习要从新知阶段的局部学习,到复习阶段的整体把握.要对所学内容进行再认识、再整合,沟通相互关系,从而达到方法、能力的升华.
结束语
初一年级 数学
二元一次方程组复习
本章知识结构图
二元
一次
方程
组
概念
解法
应用
一元一次方程
二元一次方程及解
二元一次方程组及解
消元
代入法、加减法
本章知识回顾
1.二元一次方程及其解的概念
(1)二元一次方程:
含有两个未知数,并且含有未知数的项的次数都是“1”的方程,叫二元一次方程.
标准形式:ax+by=c(a≠0,b≠0).
(一)、概念
特别要注意a≠0,b≠0.
本章知识回顾
1.二元一次方程及其解的概念
(2)二元一次方程的解:
使二元一次方程左右两边的值相等的一对未知数的值,
叫做这个二元一次方程的一个解.
(一)、概念
一般地,一个二元一次方程有无数个解.
本章知识回顾
2.二元一次方程组及其解的概念
(1)二元一次方程组:
一般地,含有相同未知数的两个二元一次方程合在一
起,就组成了一个二元一次方程组.
也就是这个方程组一共含两个未知数,含未知数的项
的次数是 “1”.
(一)、概念
本章知识回顾
2.二元一次方程组及其解的概念
(2)二元一次方程组的解:
使二元一次方程组中的两个方程左右两边的值都相等
的两个未知数的值(即两个方程的公共解),叫做二元
一次方程组的解.
(一)、概念
本章知识回顾
解二元一次方程组的基本思想是“消元”.
消元的方法有两种:代入法、加减法.
(二)、解法
每个方程组都可以用这两种方法求解,在解题时要根据方程组中未知数的系数特点,确定用哪一种方法比较简便.
本章知识回顾
当方程组中某一未知数的系数是“1”或“-1”时用代入法比较简单.
(二)、解法
一定要仔细观察方程组的特点,有时方程组中的某一部分可以看做一个“整体”,可以用“整体思想”代入,从而达到消元的目的.
本章知识回顾
(二)、解法
当方程组中同一未知数的系数相同或互为相反数时用加减法求解简单.当同一未知数系数绝对值不同,可以求系数绝对值的最小公倍数,将该未知数系数绝对值化为最小公倍数,再用加减法求解.
当方程组比较复杂时通常先进行整理,观察特点,确定求解方法,再求解.
本章知识回顾
基本思想:实际问题转化为数学问题,得到数学问题的解,
检验是否符合实际问题,从而得到实际问题的答案.
(三)、应用
关键:确定等量关系.
步骤:审、设、列、解、验、答.
典型例题
例1. 如果方程 是关于x,y的二元一次方程,则k的值是 .
分析:由未知数x的次数是“1”,得到|k|-1=1,k=±2,这是最容易出现的错误.
本题应该满足的条件是:
二元一次方程的标准形式是ax+by=c (其中a≠0,b≠0).当k-2=0时方程变成了一元一次方程.
典型例题
分析:根据二元一次方程解的定义,得到2a+2=6.
A
例2.已知 是二元一次方程ax+2y=6的一个解,那
么a的值为( ).
A.2 B.-2 C.4 D. -4
典型例题
例3.下列方程组:① ②
③ 其中是二元一次方程组的是( ).
A.①② B.②③ C.①③ D.③
分析:①含有三个未知数, ②中的第一个方程不是整式方程.
D
例4.下列x,y的各对数值中,是方程组 的解的是( ).
典型例题
A.
B.
C.
D.
分析:可以依据二元一次方程组解的定义,也可以用解方程组的方法求解问题,随着所学知识的增多,解决同一问题的方法也会增多,要学会发展地解决问题.
C
典型例题
例5.解方程组:
分析:方程组中的第一个方程有分母,第二个方程中有括
号,先把两个方程进行整理,得
用加减法或代入法求解.
典型例题
例5.解方程组:
解:整理,得
①
②
②-①,得
把y=2 代入②,得
∴方程组的解是
方法一:减法消元
y=2.
x=2.
典型例题
例5.解方程组:
解:整理,得
①
②
方法二:代入消元法
把③代入① ,得
由② ,得
③
解得
把 代入③ ,得
∴方程组的解是
典型例题
例5.解方程组:
①
②
∴方程组的解是
把x=2代入② ,得
y=2.
解:把②代入① ,得
方法三:两个方程中都有y+1,
可以整体代入消元.
典型例题
例5.解方程组:
小结:比较三种解法,观察点不同,切入点不同,选择的方法就会不同,在解题中要根据方程组特点选择恰当方法进行求解.
典型例题
例6. 当x=-3和x=2时,代数式kx+b的值分别是-4和11.
(1)求k,b的值.
(2)求x为何值时,代数式kx+b的值是0.
分析:x=-3和x=2时的值分别是-4和11代入可得关于k,b的方程组,求解即得k,b的值,代数式确定.由代数式的值是0,可得关于x的一元一次方程.
典型例题
例6. 当x=-3和x=2时,代数式kx+b的值分别是-4和11.
(1)求k,b的值.
(2)求x为何值时,代数式kx+b的值是0.
解得
∴k,b的值分别为3,5.
(2)由(1)得代数式为3x+5,根据题意,得3x+5=0.
∴ 时,代数式3x+5的值为0.
解:(1)根据题意,得
典型例题
甲同学:先解关于x,y 的方程组 ,再求k的值.
乙同学:先将方程组中的两个方程相加, 再求k的值.
丙同学:先解方程组 再求k的值.
你最欣赏哪种思路?根据你选的思路解答此题,再对选择的思路进行简要评价.
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
∵ x+y=2,
∴
解得
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
解:依照甲同学思路,解 得
典型例题
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
∵ x+y=2,
∴ 5x+5y=10.即7k+4=10.解得
①
②
解:依照乙同学思路,方程组
①+②,得
例7. 已知有理数x,y满足x+y=2
求k的值.
典型例题
∵ 3x+2y=7k-2,
∴ 7k-2=4.解得
解:依照丙同学思路,解方程组
解得
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
小结:甲的方法是解决这类问题的通法,而后两种方法是根据本题特点确定的方法.很显然乙、丙的方法计算量小,要明显优于甲同学的方法.丙和甲解法相同之处是解方程组,丙比甲巧的是重新组合方程组,解起来简单.乙的方法最巧.因此在解题中要学会处理通法与特殊方法之间的关系,选用最简单的方法.
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
小结:已知关于x,y的方程组满足 又出现与
x+y(或x-y)相关的条件,就可以直接①+②(或①-②).
①
②
例7. 已知有理数x,y满足x+y=2且满足
求k的值.
典型例题
例8. 每年的3月12日是植树节.某校七年级有183名学生参加植树节活动,在活动中男生平均每人挖3个树坑,女生平均每人种6棵树,这样恰好使挖好的树坑都能种上树.该年级参加植树的男、女生各有多少人?
分析:审题明确已知量、未知量,分析数量关系,确定等量关系.
等量关系: 男生人数+女生人数=183;
男生挖树坑总数=女生种树总数.
典型例题
等量关系: 男生人数+女生人数=183;
男生挖树坑总数=女生种树总数.
解:设七年级参加植树的男生x人,女生y人.根据题意,得
解方程组,得
答:七年级参加植树的男生122人,女生61人.
课堂小结
本章内容:
四个概念;
两种方法(代入法、加减法);
四种思想(消元、转化、化归、建模);
一个意识(应用意识).
理解概念、掌握方法、体会思想,提升意识.
作业
1.如果方程 是关于x,y的二元一次方程,则m的值是 .
2.请判断下面的两对数是不是方程2x-y=5的解.
作业
3.解下列方程组:
4.一个正方体,其中有一对相对的面上的数字之和是29,差是7,这两个数各是多少?
5. 已知关于x,y的二元一次方程组 和
的解相同,试求m,n的取值范围.
作业
数学的复习要从新知阶段的局部学习,到复习阶段的整体把握.要对所学内容进行再认识、再整合,沟通相互关系,从而达到方法、能力的升华.
结束语
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
