人教版七年级下册数学课件:6.1 平方根之 根号 2 有多大 ? (共45张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件:6.1 平方根之 根号 2 有多大 ? (共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 21:46:52 | ||
图片预览









文档简介
(共45张PPT)
初一年级 数学
根号 2 有多大 ?
知 识 回 顾
一般地,如果一个正数 x 的平方等于a,即 x2 = a,
那么这个正数 x 叫做? a 的算术平方根.
a 的算术平方根记为 ,读作“根号 a ”,
a 叫做被开方数.
规定:0的算术平方根是0.
算术平方根的概念
知 识 回 顾
算术平方根的概念
被开方数越大,对应的算术平方根也越大.
由
得
例如:
探 究 活 动
能否用两个面积为 1 dm2 的小正方形拼成一个面积为 2 dm2 的大正方形?
试一试
探 究 活 动
拼成的这个面积为 2 dm2 的大正方形的边长应该是多少呢?
思考
分析:可设大正方形的边长为 x dm ,
则
由算术平方根的意义可知
所以大正方形的边长是 dm .
?
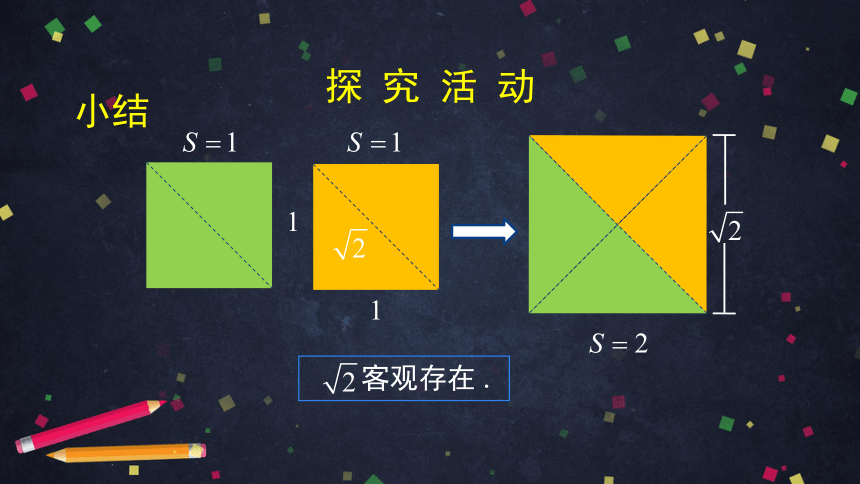
探 究 活 动
小结
客观存在 .
探 究 活 动
思考
客观存在 .
有多大呢?
由
探 究 活 动
分析
被开方数越大,对应的算术平方根也越大.
已有的知识
得
用有理数估计 的大小 .
(a,b 均为正数,且 a,b 可以
表示成有理数的平方)
(a,b 均为正数)
探 究 活 动
分析:
是整数部分是 1 的小数.
因为
所以
;
试一试
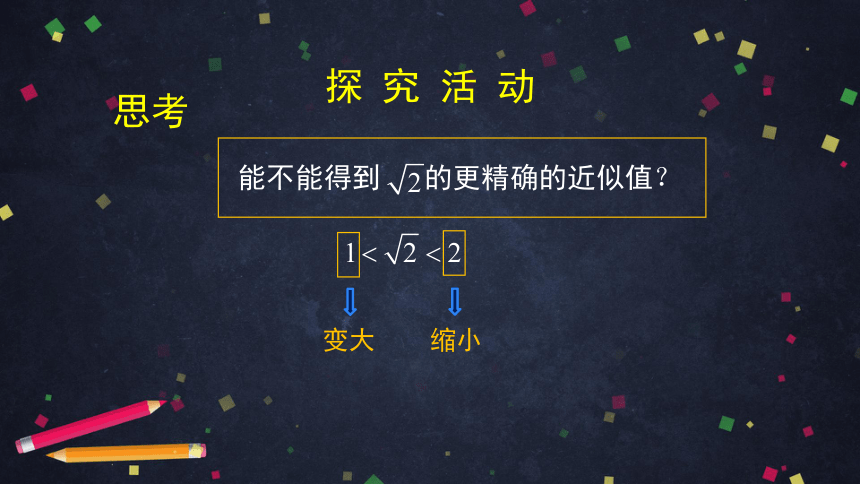
探 究 活 动
思考
变大
缩小
能不能得到 的更精确的近似值?
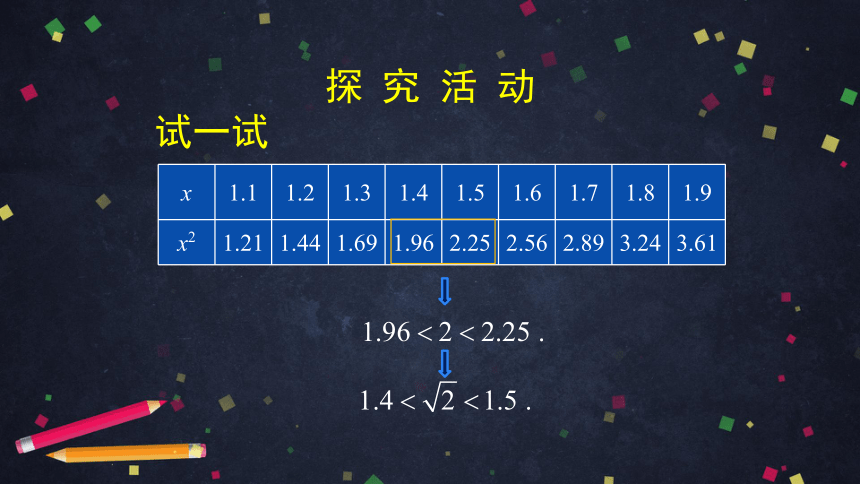
探 究 活 动
试一试
x 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
x2 1.21 1.44 1.69 1.96 2.25 2.56 2.89 3.24 3.61
探 究 活 动
因为
所以
,
分析:
探 究 活 动
试一试
x 1.41 1.42 1.43 1.44 1.45 1.46 1.47 1.48 1.49
x2
1.45
2.1025
1.42
2.0164
1.9881
探 究 活 动
所以
因为
分析:
探 究 活 动
因为
所以
能不能进一步精确
的大小?
如此进行下去,可以得到
的更精确的近似值.
小结
是无限不循环小数.
=1.414 213 562 373 ???
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
探 究 活 动
你能用刚才的方法估计 的近似值吗 ?
练一练
,
因为
所以
;
,
因为
所以
;
是无限不循环小数.
=1.732 050 807 568 ???
小 结
=1.414 213 562 373 ???
许多正有理数的算术平方根(如:
也是无限不循环小数.
)
用计算器求出一 个正有理数的算术平方根 (或其近似值).
做一做
大多数计算器都有 键,用它可以求出一个正有理数的算术平方根 (或其近似值).
依次:按键
输入正有理数
按键
显示结果
做一做
(2) (精确到 0.001).
(1) ;
用计算器求下列各式的值:
用计算器求下列各式的值:
做一做
按键
输入:3136
按键
显示:
(1) ;
所以 .
解:
56
用计算器求下列各式的值:
做一做
按键
输入: 5
按键
显示:
(2) (精确到0.001).
解:
所以 .
2.236 067 977
(1) (精确到0.001);
用计算器求下列各式的值:
试一试
(2) (精确到0.01).
许多正有理数的算术平方根是无限不循环小数.
用有理数估计像
这样的算术平方根的大小 .
小 结
用计算器求出一 个正有理数的算术平
方根 (或其近似值).
典 型 例 题
用近似值比较大小
例 比较大小:
即
所以
解:因为
例 比较大小:
典 型 例 题
用有理数估计 范围
得
解:
由
从而
典 型 例 题
例 小丽想用一块面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
典 型 例 题
思考
实 际 问 题
数 学 问 题
转 化
能否用面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3:2.
需要裁出长方形的长与正方形的边长之间的大小关系是什么?
运算
典 型 例 题
分析
面积为 400 cm2 的正方形
边长为20 cm
面积为 300 cm2 的长方形纸片,且它的长宽之比为 3:2
设两边长分别为 3x cm 和 2x cm
典 型 例 题
根据长方形的长和宽与面积的关系得
3 x ? 2 x = 300 ,
6 x2 = 300 ,
x2 = 50 ,
分析
就是
设长方形纸片的长为 3 x cm,宽 为 2 x cm .
因此长方形纸片的长为 cm .
x = .
典 型 例 题
分析
面积为 400 cm2 的正方形
边长为 20 cm
面积为 300 cm2 的长方形纸片,且它的长宽之比为3:2
长为 cm
所以
所以
典 型 例 题
比较大小: 与 20.
长方形纸片的长大于正方形纸片的边长.
分析
所以
因为
方法1:
所以
因为
方法2:
典 型 例 题
思考
实 际 问 题
数 学 问 题
转 化
能否在面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3:2.
需要裁出长方形的长与正方形的边长之间的大小关系是什么?
长方形纸片的长大于正方形纸片的边长
不 能
说 明
解:设裁出的长方形的两边长分别为 3 x cm 和 2 x cm .
根据长方形的长和宽与面积的关系得
3 x ? 2 x = 300 ,
6 x2 = 300 ,
x2 = 50 ,
x = .
因此长方形纸片的长为 cm .
典 型 例 题
典 型 例 题
由此可知 ,即长方形的纸片的长大于 21 cm .
因为 ,所以 .
因为 ,所以正方形纸片的边长是 20 cm .
答:不能同意小明的说法.小丽不能用这块
正方形纸片裁出符合要求的长方形纸片.
.
这样,长方形的纸片的长大于正方形的边长 .
(2) (精确到0.01).
(1) ;
用计算器求下列各式的值:
巩 固 练 习
(1) ;
用计算器求下列各式的值:
巩 固 练 习
依次:按键
输入:101.2036
按键
显示:10.06 ,
解:
(2) (精确到 0.01).
用计算器求下列各式的值:
巩 固 练 习
依次:按键
输入:15
按键
显示:3.872 983 346
解:
巩 固 练 习
比较下列各组数的大小:
(1) (2)
(3) (4)
巩 固 练 习
比较下列各组数的大小:
(1) (2)
解:
所以
因为
解:
所以
因为
巩 固 练 习
比较下列各组数的大小:
(3)
得 从而
解:
由
所以
巩 固 练 习
比较下列各组数的大小:
(4)
得 从而
解:
由
所以
课 堂 小 结
是无限不循环小数.
= 1.414 213 562 373 ???
被开方数越大,对应的算术平方根也越大 .
课 后 作 业
(精确到0.01);
1. 用计算器求下列各式的值:
(2) (精确到0.001).
(1) ;
(2) .
2.比较下列各组数的大小:
同 学 们 再 见!
初一年级 数学
根号 2 有多大 ?
知 识 回 顾
一般地,如果一个正数 x 的平方等于a,即 x2 = a,
那么这个正数 x 叫做? a 的算术平方根.
a 的算术平方根记为 ,读作“根号 a ”,
a 叫做被开方数.
规定:0的算术平方根是0.
算术平方根的概念
知 识 回 顾
算术平方根的概念
被开方数越大,对应的算术平方根也越大.
由
得
例如:
探 究 活 动
能否用两个面积为 1 dm2 的小正方形拼成一个面积为 2 dm2 的大正方形?
试一试
探 究 活 动
拼成的这个面积为 2 dm2 的大正方形的边长应该是多少呢?
思考
分析:可设大正方形的边长为 x dm ,
则
由算术平方根的意义可知
所以大正方形的边长是 dm .
?
探 究 活 动
小结
客观存在 .
探 究 活 动
思考
客观存在 .
有多大呢?
由
探 究 活 动
分析
被开方数越大,对应的算术平方根也越大.
已有的知识
得
用有理数估计 的大小 .
(a,b 均为正数,且 a,b 可以
表示成有理数的平方)
(a,b 均为正数)
探 究 活 动
分析:
是整数部分是 1 的小数.
因为
所以
;
试一试
探 究 活 动
思考
变大
缩小
能不能得到 的更精确的近似值?
探 究 活 动
试一试
x 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
x2 1.21 1.44 1.69 1.96 2.25 2.56 2.89 3.24 3.61
探 究 活 动
因为
所以
,
分析:
探 究 活 动
试一试
x 1.41 1.42 1.43 1.44 1.45 1.46 1.47 1.48 1.49
x2
1.45
2.1025
1.42
2.0164
1.9881
探 究 活 动
所以
因为
分析:
探 究 活 动
因为
所以
能不能进一步精确
的大小?
如此进行下去,可以得到
的更精确的近似值.
小结
是无限不循环小数.
=1.414 213 562 373 ???
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
探 究 活 动
你能用刚才的方法估计 的近似值吗 ?
练一练
,
因为
所以
;
,
因为
所以
;
是无限不循环小数.
=1.732 050 807 568 ???
小 结
=1.414 213 562 373 ???
许多正有理数的算术平方根(如:
也是无限不循环小数.
)
用计算器求出一 个正有理数的算术平方根 (或其近似值).
做一做
大多数计算器都有 键,用它可以求出一个正有理数的算术平方根 (或其近似值).
依次:按键
输入正有理数
按键
显示结果
做一做
(2) (精确到 0.001).
(1) ;
用计算器求下列各式的值:
用计算器求下列各式的值:
做一做
按键
输入:3136
按键
显示:
(1) ;
所以 .
解:
56
用计算器求下列各式的值:
做一做
按键
输入: 5
按键
显示:
(2) (精确到0.001).
解:
所以 .
2.236 067 977
(1) (精确到0.001);
用计算器求下列各式的值:
试一试
(2) (精确到0.01).
许多正有理数的算术平方根是无限不循环小数.
用有理数估计像
这样的算术平方根的大小 .
小 结
用计算器求出一 个正有理数的算术平
方根 (或其近似值).
典 型 例 题
用近似值比较大小
例 比较大小:
即
所以
解:因为
例 比较大小:
典 型 例 题
用有理数估计 范围
得
解:
由
从而
典 型 例 题
例 小丽想用一块面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
典 型 例 题
思考
实 际 问 题
数 学 问 题
转 化
能否用面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3:2.
需要裁出长方形的长与正方形的边长之间的大小关系是什么?
运算
典 型 例 题
分析
面积为 400 cm2 的正方形
边长为20 cm
面积为 300 cm2 的长方形纸片,且它的长宽之比为 3:2
设两边长分别为 3x cm 和 2x cm
典 型 例 题
根据长方形的长和宽与面积的关系得
3 x ? 2 x = 300 ,
6 x2 = 300 ,
x2 = 50 ,
分析
就是
设长方形纸片的长为 3 x cm,宽 为 2 x cm .
因此长方形纸片的长为 cm .
x = .
典 型 例 题
分析
面积为 400 cm2 的正方形
边长为 20 cm
面积为 300 cm2 的长方形纸片,且它的长宽之比为3:2
长为 cm
所以
所以
典 型 例 题
比较大小: 与 20.
长方形纸片的长大于正方形纸片的边长.
分析
所以
因为
方法1:
所以
因为
方法2:
典 型 例 题
思考
实 际 问 题
数 学 问 题
转 化
能否在面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3:2.
需要裁出长方形的长与正方形的边长之间的大小关系是什么?
长方形纸片的长大于正方形纸片的边长
不 能
说 明
解:设裁出的长方形的两边长分别为 3 x cm 和 2 x cm .
根据长方形的长和宽与面积的关系得
3 x ? 2 x = 300 ,
6 x2 = 300 ,
x2 = 50 ,
x = .
因此长方形纸片的长为 cm .
典 型 例 题
典 型 例 题
由此可知 ,即长方形的纸片的长大于 21 cm .
因为 ,所以 .
因为 ,所以正方形纸片的边长是 20 cm .
答:不能同意小明的说法.小丽不能用这块
正方形纸片裁出符合要求的长方形纸片.
.
这样,长方形的纸片的长大于正方形的边长 .
(2) (精确到0.01).
(1) ;
用计算器求下列各式的值:
巩 固 练 习
(1) ;
用计算器求下列各式的值:
巩 固 练 习
依次:按键
输入:101.2036
按键
显示:10.06 ,
解:
(2) (精确到 0.01).
用计算器求下列各式的值:
巩 固 练 习
依次:按键
输入:15
按键
显示:3.872 983 346
解:
巩 固 练 习
比较下列各组数的大小:
(1) (2)
(3) (4)
巩 固 练 习
比较下列各组数的大小:
(1) (2)
解:
所以
因为
解:
所以
因为
巩 固 练 习
比较下列各组数的大小:
(3)
得 从而
解:
由
所以
巩 固 练 习
比较下列各组数的大小:
(4)
得 从而
解:
由
所以
课 堂 小 结
是无限不循环小数.
= 1.414 213 562 373 ???
被开方数越大,对应的算术平方根也越大 .
课 后 作 业
(精确到0.01);
1. 用计算器求下列各式的值:
(2) (精确到0.001).
(1) ;
(2) .
2.比较下列各组数的大小:
同 学 们 再 见!
