北京版七年级下册数学课件:5.6 二元一次方程组的应用(第1课时) (共36张PPT)
文档属性
| 名称 | 北京版七年级下册数学课件:5.6 二元一次方程组的应用(第1课时) (共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 21:48:22 | ||
图片预览








文档简介
(共36张PPT)
初一年级 数学
二元一次方程组的应用(第1课时)
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显但十分有趣.《孙子算经》下卷第31题“鸡兔同笼”流传广泛,甚至漂洋过海流传到了日本等国.今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
创设情境 引发思考
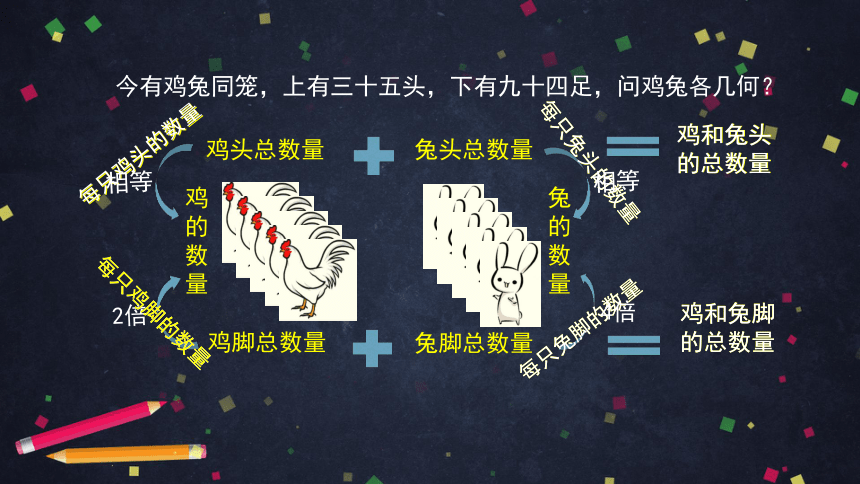
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
提出问题 初步探索
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
鸡和兔头
的总数量
鸡和兔脚
的总数量
每只鸡头的数量
每只鸡脚的数量
每只兔脚的数量
每只兔头的数量
鸡和兔头
的总数量
鸡和兔脚
的总数量
相等
2倍
相等
4倍
每只鸡头的数量
每只鸡脚的数量
每只兔头的数量
每只兔脚的数量
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
算术法:
法1.鸡为 ,兔为 35-23=12.
法2.兔为 ,鸡为 35-12=23.
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
鸡和兔头
的总数量
鸡和兔脚
的总数量
相等
2倍
4倍
相等
35
94
2x
35-x
4(35-x)
x
x
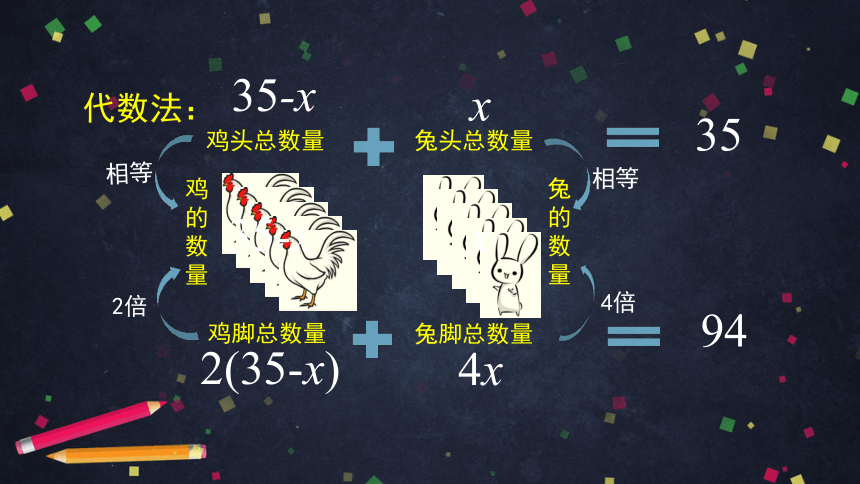
代数法:
35-x
解:设笼中有鸡 x 只,兔 只,根据题意,得
解这个方程,得
答:笼中鸡有23只,兔有12只.
列一元一次方程:
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
相等
2倍
4倍
相等
35
94
x
4x
35-x
35-x
代数法:
x
2(35-x)
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
相等
2倍
4倍
相等
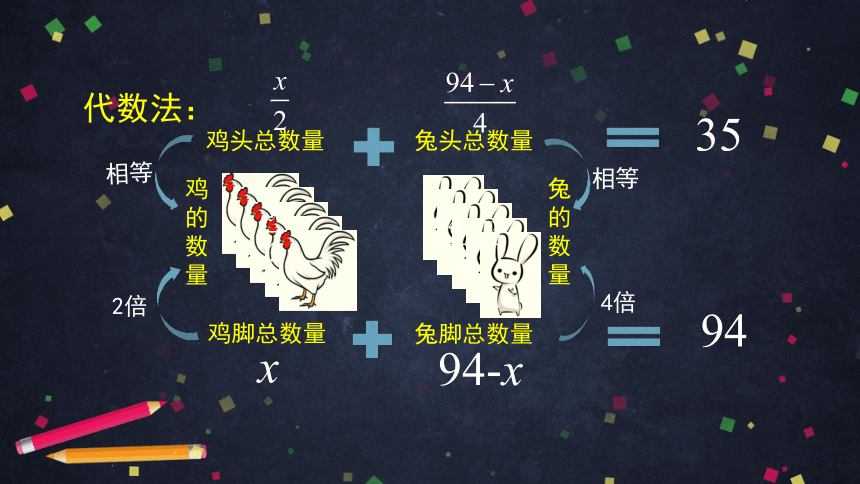
35
94
x
94-x
代数法:
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
相等
2倍
4倍
相等
35
94
2x
y
4y
x
x
代数法:
y
解:设笼中有鸡 x 只,兔 y 只,根据题意,得
由?,得 ?
把?代入?,得
把 代入?,得
答:笼中鸡有23只,兔有12只.
列
二
元
一
次
方
程
组
设
列
解
验
答
审
?
?
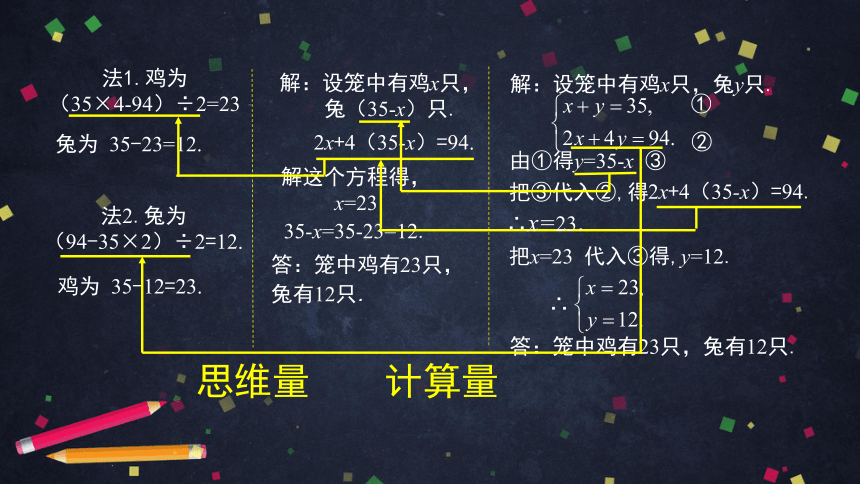
法1.鸡为
(35×4-94)÷2=23
解:设笼中有鸡x只,
兔(35-x)只.
解:设笼中有鸡x只,兔y只.
法2.兔为
(94-35×2)÷2=12.
2x+4(35-x)=94.
解这个方程得,
x=23
35-x=35-23=12.
∴
答:笼中鸡有23只,兔有12只.
①
由①得y=35-x .③
把③代入②,得
把x=23 代入③得,y=12.
鸡为 35-12=23.
兔为 35-23=12.
思维量
计算量
答:笼中鸡有23只,
兔有12只.
②
∴x=23.
2x+4(35-x)=94.
例. 某中学为响应习主席提出的“足球进校园”的号召,开设了“足球大课间活动”,若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买
A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
继续探索 深化认识
问题1. 请说出题中有哪些量?哪些是已知量?哪些是未知量?
这些量之间有什么关系?
例.若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
例.若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
A品牌单价
B品牌单价
A品牌个数
B品牌个数
总价4500
A品牌总价
B品牌总价
总价4800
×
×
=
=
x
y
50x
25y
40x
35y
50
25
40
35
解:设A品牌足球1个 x 元,B品牌足球1个 y 元,依题得
原方程组可化为
?×7-?,得
把 代入?,得
答:A品牌足球1个50元,B品牌足球1个80元.
?
?
实际问题
数学问题
(二元一次方程组)
数学问题的解
(二元一次方程组的解)
问题答案
设未知数,列方程组
代入法
加减法
(消元)
解
方
程
组
检验
问2.为什么不用一元一次方程来解?
若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
A品牌单价
B品牌单价
A品牌个数
B品牌个数
总价4500
A品牌总价
B品牌总价
总价4800
×
×
x
50x
40x
50
25
40
35
问3. 通过以上探索,你认为列二元一次方程组
和列一元一次方程解决实际问题有哪些相
同点和不同点?
实际问题
数学问题
【一次方程(组)】
数学问题的解
【方程(组)的解】
问题答案
设未知数,列方程(组)
解方程(组)
检验
例.被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1只雀重量
1只燕重量
雀的数量
燕的数量
5只雀重量
6只燕重量
5只雀6只燕的总重量
交换前
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1只雀重量
1只燕重量
雀的数量
燕的数量
4只雀重量
5只燕重量
5只雀重量
6只燕重量
5只雀6只燕的总重量
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1只雀重量
1只燕重量
雀的数量
燕的数量
4只雀重量
5只燕重量
5只雀重量
6只燕重量
5只雀6只燕的总重量
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
5只雀重量
6只燕重量
1
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
5只雀重量
6只燕重量
1
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
设每只雀重 x 斤,每只燕重 y 斤
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
设每只雀重 x 斤,每只燕重 y 斤
5x
6y
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1
交换前
交换后
设每只雀重 x 斤,每只燕重 y 斤
4x+y
5y+x
5x
6y
解:设每只雀重 x 斤,每只燕重 y 斤,依题得
解这个方程组,得
答:每只雀重 斤,每只燕重 斤.
?
?
课堂小结 总结提升
1.本节课你学习了什么知识?
实际问题
算术法
列一元一次方程
列二元一次方程组
优越性
联系
(审、设、列、解、验、答)
实际问题
数学问题
(二元一次方程组)
数学问题的解
(二元一次方程组的解)
问题答案
设未知数,列方程组
代入法
加减法
(消元)
解
方
程
组
检验
2.本节课你感受到了哪些数学思想和方法?
转化
建模
3.本节课的研究过程给你学习带来什么启示呢?
巩固运用 内化新知
1.李威喜欢集邮,他有中国邮票和外国邮票共335张,其中中国邮票的张数比外国邮票的张数的3倍少17张.他有中国邮票和外国邮票各多少张?
巩固运用 内化新知
2.某校七年级(1)、(2)班两班同学积极参加全民健身活动,为此两班到同一商店购买体育用品.已知七年级(1)班购买了3个篮球和8个羽毛球拍共用了442元.七年级(2)班购买了同样的5个篮球和6个羽毛球拍共用了480元.问每个篮球和每个羽毛球拍各多少元?
谢谢观看!
初一年级 数学
二元一次方程组的应用(第1课时)
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显但十分有趣.《孙子算经》下卷第31题“鸡兔同笼”流传广泛,甚至漂洋过海流传到了日本等国.今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
创设情境 引发思考
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
提出问题 初步探索
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
鸡和兔头
的总数量
鸡和兔脚
的总数量
每只鸡头的数量
每只鸡脚的数量
每只兔脚的数量
每只兔头的数量
鸡和兔头
的总数量
鸡和兔脚
的总数量
相等
2倍
相等
4倍
每只鸡头的数量
每只鸡脚的数量
每只兔头的数量
每只兔脚的数量
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
算术法:
法1.鸡为 ,兔为 35-23=12.
法2.兔为 ,鸡为 35-12=23.
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
鸡和兔头
的总数量
鸡和兔脚
的总数量
相等
2倍
4倍
相等
35
94
2x
35-x
4(35-x)
x
x
代数法:
35-x
解:设笼中有鸡 x 只,兔 只,根据题意,得
解这个方程,得
答:笼中鸡有23只,兔有12只.
列一元一次方程:
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
相等
2倍
4倍
相等
35
94
x
4x
35-x
35-x
代数法:
x
2(35-x)
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
相等
2倍
4倍
相等
35
94
x
94-x
代数法:
鸡头总数量
兔头总数量
鸡
的
数
量
兔的
数
量
鸡脚总数量
兔脚总数量
相等
2倍
4倍
相等
35
94
2x
y
4y
x
x
代数法:
y
解:设笼中有鸡 x 只,兔 y 只,根据题意,得
由?,得 ?
把?代入?,得
把 代入?,得
答:笼中鸡有23只,兔有12只.
列
二
元
一
次
方
程
组
设
列
解
验
答
审
?
?
法1.鸡为
(35×4-94)÷2=23
解:设笼中有鸡x只,
兔(35-x)只.
解:设笼中有鸡x只,兔y只.
法2.兔为
(94-35×2)÷2=12.
2x+4(35-x)=94.
解这个方程得,
x=23
35-x=35-23=12.
∴
答:笼中鸡有23只,兔有12只.
①
由①得y=35-x .③
把③代入②,得
把x=23 代入③得,y=12.
鸡为 35-12=23.
兔为 35-23=12.
思维量
计算量
答:笼中鸡有23只,
兔有12只.
②
∴x=23.
2x+4(35-x)=94.
例. 某中学为响应习主席提出的“足球进校园”的号召,开设了“足球大课间活动”,若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买
A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
继续探索 深化认识
问题1. 请说出题中有哪些量?哪些是已知量?哪些是未知量?
这些量之间有什么关系?
例.若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
例.若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
A品牌单价
B品牌单价
A品牌个数
B品牌个数
总价4500
A品牌总价
B品牌总价
总价4800
×
×
=
=
x
y
50x
25y
40x
35y
50
25
40
35
解:设A品牌足球1个 x 元,B品牌足球1个 y 元,依题得
原方程组可化为
?×7-?,得
把 代入?,得
答:A品牌足球1个50元,B品牌足球1个80元.
?
?
实际问题
数学问题
(二元一次方程组)
数学问题的解
(二元一次方程组的解)
问题答案
设未知数,列方程组
代入法
加减法
(消元)
解
方
程
组
检验
问2.为什么不用一元一次方程来解?
若购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元;若购买A种品牌的足球40个,B种品牌的足球35个,共花费4800元.求A、B两种品牌足球的单价各多少元?
A品牌单价
B品牌单价
A品牌个数
B品牌个数
总价4500
A品牌总价
B品牌总价
总价4800
×
×
x
50x
40x
50
25
40
35
问3. 通过以上探索,你认为列二元一次方程组
和列一元一次方程解决实际问题有哪些相
同点和不同点?
实际问题
数学问题
【一次方程(组)】
数学问题的解
【方程(组)的解】
问题答案
设未知数,列方程(组)
解方程(组)
检验
例.被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1只雀重量
1只燕重量
雀的数量
燕的数量
5只雀重量
6只燕重量
5只雀6只燕的总重量
交换前
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1只雀重量
1只燕重量
雀的数量
燕的数量
4只雀重量
5只燕重量
5只雀重量
6只燕重量
5只雀6只燕的总重量
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1只雀重量
1只燕重量
雀的数量
燕的数量
4只雀重量
5只燕重量
5只雀重量
6只燕重量
5只雀6只燕的总重量
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
5只雀重量
6只燕重量
1
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
5只雀重量
6只燕重量
1
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
设每只雀重 x 斤,每只燕重 y 斤
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1
交换前
交换后
4只雀和1只燕的总重量
5只燕和1只雀的总重量
设每只雀重 x 斤,每只燕重 y 斤
5x
6y
今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?
1
交换前
交换后
设每只雀重 x 斤,每只燕重 y 斤
4x+y
5y+x
5x
6y
解:设每只雀重 x 斤,每只燕重 y 斤,依题得
解这个方程组,得
答:每只雀重 斤,每只燕重 斤.
?
?
课堂小结 总结提升
1.本节课你学习了什么知识?
实际问题
算术法
列一元一次方程
列二元一次方程组
优越性
联系
(审、设、列、解、验、答)
实际问题
数学问题
(二元一次方程组)
数学问题的解
(二元一次方程组的解)
问题答案
设未知数,列方程组
代入法
加减法
(消元)
解
方
程
组
检验
2.本节课你感受到了哪些数学思想和方法?
转化
建模
3.本节课的研究过程给你学习带来什么启示呢?
巩固运用 内化新知
1.李威喜欢集邮,他有中国邮票和外国邮票共335张,其中中国邮票的张数比外国邮票的张数的3倍少17张.他有中国邮票和外国邮票各多少张?
巩固运用 内化新知
2.某校七年级(1)、(2)班两班同学积极参加全民健身活动,为此两班到同一商店购买体育用品.已知七年级(1)班购买了3个篮球和8个羽毛球拍共用了442元.七年级(2)班购买了同样的5个篮球和6个羽毛球拍共用了480元.问每个篮球和每个羽毛球拍各多少元?
谢谢观看!
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
