四年级下册数学提升课件-第7单元 三角形、平行四边形和梯形-苏教版(共47张PPT)
文档属性
| 名称 | 四年级下册数学提升课件-第7单元 三角形、平行四边形和梯形-苏教版(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 09:11:31 | ||
图片预览











文档简介
(共47张PPT)
提升拓展课件
江苏版四年级下
第1课时 三角形的认识
三角形在生活中的应用
1.选一选。
(1)下列选项中,( )没有运用到三角形的稳定性的特性。
A.自行车的三角形车架
B.长方形门框的斜拉条
C.电动伸缩门
C
1.选一选。
(2)下列建筑中,( )运用了三角形的稳定性的特性。
A.厦门市海沧大桥 B.广西玉林真武阁
C.西宁青海宾馆
A
2.在三角形采摘园中,要从顶点A向对边铺一条最短的路,请你画出来,并说明理由。
从点A到BC的垂直线段最短
第2课时 三角形三边的关系
根据三角形三边关系
解决三角形问题
1.把一根长15 cm的吸管剪成3段,再用这三段吸管围成一个三角形,可以怎样剪?(每段都是整厘米数)
1 cm,7 cm,7 cm 2 cm,6 cm,7 cm 3 cm,6 cm,6 cm 3 cm,5 cm,7 cm 4 cm,4 cm,7 cm 4 cm,5 cm,6 cm 5 cm,5 cm,5 cm 有7种剪法
已知三角形两条边的
长度,求第三边长度
2.如果一个三角形两条边的长度分别是5 cm和9 cm,第三条边的长度是整厘米数,那么第三条边的长度可能是多少?最长是多少?最短是多少?
可能是:5 cm,6 cm,7 cm,8 cm,9 cm,10 cm,11 cm,12 cm,13 cm 最长:5+9-1=13(cm),最短:9-5+1=5(cm)
利用三角形三边关系
解决实际问题
3.解决问题。
(1)轩轩从家去超市有几条路线?哪一条路线最近?你是怎样想的?
有三条路线,走路线3最近,因为三角形两边长度之和大于第三边长。
(2)轩轩从家走到学校去上学,放学后去超市买文具,之后从超市回家。轩轩一共走了多少米?
834+518+602=1954(米)
答:轩轩一共走了1954米。
第3课时 三角形的内角和
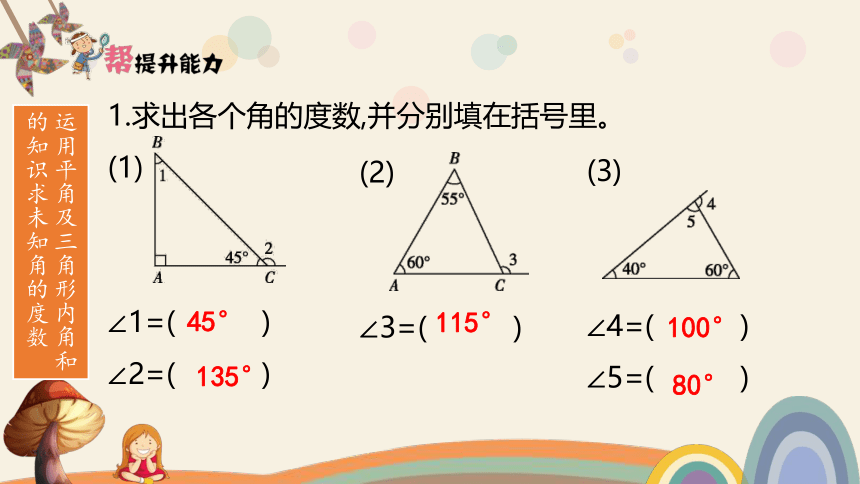
1.求出各个角的度数,并分别填在括号里。
(1)
∠1=( )
∠2=( )
(3)
∠4=( )
∠5=( )
(2)
∠3=( )
运用平角及三角形内角和
的知识求未知角的度数
45°
135°
115°
100°
80°
运用三角形的内角和的
知识解决求角的度数问题
2.一个直角三角形中,两个锐角的度数差是20°,这两个锐角分别是多少度?
(90°-20°)÷2=35°
35°+20°=55°
答:这两个锐角分别是35°,55°。
3.在三角形ABC中,已知∠A=90°,∠B的度数是∠C的2倍,求∠B,∠C的度数。
∠C=90°÷(2+1)=30°
∠B=30°×2=60°
4.在三角形ABC中,∠A的度数是∠B度数的2倍,∠C的度数是∠B度数的3倍,求∠A,∠B,∠C的度数。
∠B=180°÷(2+3+1)=30°
∠A=30°×2=60°
∠C=30°×3=90°
5.在下图中,∠1=60°,∠2=∠3,求∠4的度数。
∠2+∠3=90°-∠1=30°
∠2=∠3=30°÷2=15°
∠4=90°-15°=75°
6.下面是由一副三角尺拼成的图形,请你算出∠1的度数。
∠1=75°
第4课时 三角形的分类
1.下图中的三角形都被一张纸遮住了一部分。你能判断出它们各是什么三角形吗?
按图猜三角形问题
①钝角、直角或锐角三角形
②钝角三角形
③直角三角形
第5课时 等腰三角形和等边三角形
1.在下面的点子图中按要求画出三角形。
(1)三个角都是锐角的等腰三角形。
(2)有一个角是直角的等腰三角形。
(3)有一个角是钝角的等腰三角形。
运用等腰三角形的特征
解决问题
图形不唯一
2.如图所示,已知AB=AC,求∠1,∠2,∠3各是多少度。
∠2=180°-70°=110°
∠1=∠3=(180°-110°)÷2=35°
腰/厘米 7
腰/厘米 6
底/厘米 8
3.用一根18厘米长的吸管,围成一个等腰三角形,可以怎样围?填一填。(每条边都是整厘米数)
7
4
6
6
5
5
8
8
2
4.红领巾是少先队员的标志,它代表红旗的一角,是革命先烈的鲜血染成的,它是一个等腰三角形,小号红领巾的周长是220 cm,其中一边长为60 cm,你知道它的另外两条边的长度吗?若它其中一个角是30°,另外两个角的度数分别是多少?
220-60×2=100(cm)
180°-30°×2=120°
另外两条边长分别为60 cm,100 cm,另外两个角的度数分别是30°和120°。
5.王大爷家有一块等腰三角形的菜园,其中两条边长分别为10米和5米,要在菜园周围围上篱笆,篱笆的长至少是多少米?
10×2+5=25(米)
答:篱笆的长至少是25米。
6.一个等腰三角形的底角的度数是顶角度数的2倍,这个等腰三角形的顶角是多少度?按角分,它是一个什么三角形?
180°÷(2+2+1)=36°
36°×2=72°
三个角分别是36°,72°,72°,因此是锐角三角形。
第6课时 认识平行四边形
1.按要求在下面的点子图上画平行四边形。(每相邻两个点之间的距离是1厘米)
(1)画一个底和高都是4厘米的平行四边形。
(2)画一个底是5厘米,高是3厘米的平行四边形。
在点子图上画指定的
平行四边形
答案不唯一
2.把一个平行四边形拉成长方形,它们的周长和面积之间有什么关系?
平行四边形和长方形的关系
周长不变,面积变大了。
3.给一个平行四边形人工湖的四周围上栏杆,一共围了152米栏杆,其中一条边长为42米,则与它相邻的一条边长是多少米?
已知平行四边形周长求边长
(152-42×2)÷2=34(米)
答:与它相邻的一条边长是34米。
第7课时 认识梯形
1.填一填。
(1)当梯形的上底和下底相等时,就变成了( )。
(2)用两个完全一样的梯形可以拼成一个( )。
(3)一个梯形的上底是3厘米,如果将上底缩短3厘米,这个梯形变成了一个( )。
等腰梯形特征的综合应用
平行四边形
平行四边形
三角形
2.填一填。
(4)当梯形的一条腰( )于上、下底时,这个梯形就是直角梯形。
(5)右图中,梯形的上底是( )cm,下底是
( )cm,高是( )cm。
垂直
3
6
4
3.在下面的方格纸上画一个上底是4,下底是6,高是4的梯形,再画一个高是5的等腰梯形,每个方格的边长都是1。
在方格纸上画指定的梯形
答案不唯一。
4.(1)在下面的梯形中画两条线段,把它分成一个平行四边形、一个梯形和一个直角三角形。
(2)把它分成一个平行四边形和一个梯形。
梯形的分割问题
答案不唯一
答案不唯一
4. (3)把它分成两个完全一样的梯形。
(4)把它分成一个锐角三角形和一个钝角三角形。
答案不唯一
5.把下面的平行四边形分成两个完全一样的梯形,并填空。
(1)一个平行四边形可以分成两个( )
的梯形。两个完全一样的梯形可以拼成一个
( )。
梯形和平行四边形的联系
完全一样
平行四边形
(2)分成的梯形的上、下底的和与平行四边形的底的长
度( ),分成的梯形的高与平行四边形的高
( )。分成的其中一个梯形的面积是平行四边形面积的( )。
(3)将两个上底为5厘米,下底为7厘米,高为3厘米的梯形拼成一个平行四边形,这个平行四边形的底是
( )厘米,高是( )厘米。
相等
相等
一半
12
3
6.解决问题。
(1)“桂林山水甲天下”,漓江风光素有百里画廊之美称。为防止水患发生,在漓江上游修筑了防洪堤,其截面为等腰梯形。如下图,该梯形周长为51米,下底长比上底长的3倍还多3米,其腰长为多少米?
利用梯形的特征解决问题
[51-6-(6×3+3)]÷2=12(米)
答:其腰长为12米。
(2)用两个完全一样的直角梯形拼成一个长方形(如下图所示),直角梯形的上底是12厘米,下底是18厘米,高是8厘米,拼成的长方形的面积是多少平方厘米?
(12+18)×8=240(平方厘米)
答:拼成的长方形的面积是240平方厘米。
(3)王奶奶在自家院子中靠墙(墙足够长)围了一块梯形菜地(如下图所示)。梯形上底长2米,下底长3米,一条腰长4米,她要在菜地周围围上篱笆,10米长够吗?为什么?
2+3+4=9(米)
10>9
够了
7.数一数下面的图形中各有几个平行四边形和梯形。
平行四边形( )个 平行四边形( )个
梯形( )个 梯形( )个
运用组合法解决图形的问题
6
12
12
10
多边形的内角和
1.填一填。
(1)当多边形边数增加时,它的内角和会随着( ),如果多边形的边数增加一条,内角和就增加( )°,所以五边形的内角和比四边形多( )°。
(2)( )边形的内角和是六边形内角和的2倍;( )边形的内角和可以用7×180°来计算。
运用多边形内角和的
计算方法解决问题
增加
180
180
十
九
(3)一个多边形的边数增加4,则它的内角和增加( )°。
(4)一个多边形的内角和是1800°,则这个多边形是
( )边形。
(5)一个八边形,它每个角的度数都相等,则每个角的度数都是( )。
720
十二
135°
谢谢观赏
谢谢观赏
谢谢观赏
提升拓展课件
江苏版四年级下
第1课时 三角形的认识
三角形在生活中的应用
1.选一选。
(1)下列选项中,( )没有运用到三角形的稳定性的特性。
A.自行车的三角形车架
B.长方形门框的斜拉条
C.电动伸缩门
C
1.选一选。
(2)下列建筑中,( )运用了三角形的稳定性的特性。
A.厦门市海沧大桥 B.广西玉林真武阁
C.西宁青海宾馆
A
2.在三角形采摘园中,要从顶点A向对边铺一条最短的路,请你画出来,并说明理由。
从点A到BC的垂直线段最短
第2课时 三角形三边的关系
根据三角形三边关系
解决三角形问题
1.把一根长15 cm的吸管剪成3段,再用这三段吸管围成一个三角形,可以怎样剪?(每段都是整厘米数)
1 cm,7 cm,7 cm 2 cm,6 cm,7 cm 3 cm,6 cm,6 cm 3 cm,5 cm,7 cm 4 cm,4 cm,7 cm 4 cm,5 cm,6 cm 5 cm,5 cm,5 cm 有7种剪法
已知三角形两条边的
长度,求第三边长度
2.如果一个三角形两条边的长度分别是5 cm和9 cm,第三条边的长度是整厘米数,那么第三条边的长度可能是多少?最长是多少?最短是多少?
可能是:5 cm,6 cm,7 cm,8 cm,9 cm,10 cm,11 cm,12 cm,13 cm 最长:5+9-1=13(cm),最短:9-5+1=5(cm)
利用三角形三边关系
解决实际问题
3.解决问题。
(1)轩轩从家去超市有几条路线?哪一条路线最近?你是怎样想的?
有三条路线,走路线3最近,因为三角形两边长度之和大于第三边长。
(2)轩轩从家走到学校去上学,放学后去超市买文具,之后从超市回家。轩轩一共走了多少米?
834+518+602=1954(米)
答:轩轩一共走了1954米。
第3课时 三角形的内角和
1.求出各个角的度数,并分别填在括号里。
(1)
∠1=( )
∠2=( )
(3)
∠4=( )
∠5=( )
(2)
∠3=( )
运用平角及三角形内角和
的知识求未知角的度数
45°
135°
115°
100°
80°
运用三角形的内角和的
知识解决求角的度数问题
2.一个直角三角形中,两个锐角的度数差是20°,这两个锐角分别是多少度?
(90°-20°)÷2=35°
35°+20°=55°
答:这两个锐角分别是35°,55°。
3.在三角形ABC中,已知∠A=90°,∠B的度数是∠C的2倍,求∠B,∠C的度数。
∠C=90°÷(2+1)=30°
∠B=30°×2=60°
4.在三角形ABC中,∠A的度数是∠B度数的2倍,∠C的度数是∠B度数的3倍,求∠A,∠B,∠C的度数。
∠B=180°÷(2+3+1)=30°
∠A=30°×2=60°
∠C=30°×3=90°
5.在下图中,∠1=60°,∠2=∠3,求∠4的度数。
∠2+∠3=90°-∠1=30°
∠2=∠3=30°÷2=15°
∠4=90°-15°=75°
6.下面是由一副三角尺拼成的图形,请你算出∠1的度数。
∠1=75°
第4课时 三角形的分类
1.下图中的三角形都被一张纸遮住了一部分。你能判断出它们各是什么三角形吗?
按图猜三角形问题
①钝角、直角或锐角三角形
②钝角三角形
③直角三角形
第5课时 等腰三角形和等边三角形
1.在下面的点子图中按要求画出三角形。
(1)三个角都是锐角的等腰三角形。
(2)有一个角是直角的等腰三角形。
(3)有一个角是钝角的等腰三角形。
运用等腰三角形的特征
解决问题
图形不唯一
2.如图所示,已知AB=AC,求∠1,∠2,∠3各是多少度。
∠2=180°-70°=110°
∠1=∠3=(180°-110°)÷2=35°
腰/厘米 7
腰/厘米 6
底/厘米 8
3.用一根18厘米长的吸管,围成一个等腰三角形,可以怎样围?填一填。(每条边都是整厘米数)
7
4
6
6
5
5
8
8
2
4.红领巾是少先队员的标志,它代表红旗的一角,是革命先烈的鲜血染成的,它是一个等腰三角形,小号红领巾的周长是220 cm,其中一边长为60 cm,你知道它的另外两条边的长度吗?若它其中一个角是30°,另外两个角的度数分别是多少?
220-60×2=100(cm)
180°-30°×2=120°
另外两条边长分别为60 cm,100 cm,另外两个角的度数分别是30°和120°。
5.王大爷家有一块等腰三角形的菜园,其中两条边长分别为10米和5米,要在菜园周围围上篱笆,篱笆的长至少是多少米?
10×2+5=25(米)
答:篱笆的长至少是25米。
6.一个等腰三角形的底角的度数是顶角度数的2倍,这个等腰三角形的顶角是多少度?按角分,它是一个什么三角形?
180°÷(2+2+1)=36°
36°×2=72°
三个角分别是36°,72°,72°,因此是锐角三角形。
第6课时 认识平行四边形
1.按要求在下面的点子图上画平行四边形。(每相邻两个点之间的距离是1厘米)
(1)画一个底和高都是4厘米的平行四边形。
(2)画一个底是5厘米,高是3厘米的平行四边形。
在点子图上画指定的
平行四边形
答案不唯一
2.把一个平行四边形拉成长方形,它们的周长和面积之间有什么关系?
平行四边形和长方形的关系
周长不变,面积变大了。
3.给一个平行四边形人工湖的四周围上栏杆,一共围了152米栏杆,其中一条边长为42米,则与它相邻的一条边长是多少米?
已知平行四边形周长求边长
(152-42×2)÷2=34(米)
答:与它相邻的一条边长是34米。
第7课时 认识梯形
1.填一填。
(1)当梯形的上底和下底相等时,就变成了( )。
(2)用两个完全一样的梯形可以拼成一个( )。
(3)一个梯形的上底是3厘米,如果将上底缩短3厘米,这个梯形变成了一个( )。
等腰梯形特征的综合应用
平行四边形
平行四边形
三角形
2.填一填。
(4)当梯形的一条腰( )于上、下底时,这个梯形就是直角梯形。
(5)右图中,梯形的上底是( )cm,下底是
( )cm,高是( )cm。
垂直
3
6
4
3.在下面的方格纸上画一个上底是4,下底是6,高是4的梯形,再画一个高是5的等腰梯形,每个方格的边长都是1。
在方格纸上画指定的梯形
答案不唯一。
4.(1)在下面的梯形中画两条线段,把它分成一个平行四边形、一个梯形和一个直角三角形。
(2)把它分成一个平行四边形和一个梯形。
梯形的分割问题
答案不唯一
答案不唯一
4. (3)把它分成两个完全一样的梯形。
(4)把它分成一个锐角三角形和一个钝角三角形。
答案不唯一
5.把下面的平行四边形分成两个完全一样的梯形,并填空。
(1)一个平行四边形可以分成两个( )
的梯形。两个完全一样的梯形可以拼成一个
( )。
梯形和平行四边形的联系
完全一样
平行四边形
(2)分成的梯形的上、下底的和与平行四边形的底的长
度( ),分成的梯形的高与平行四边形的高
( )。分成的其中一个梯形的面积是平行四边形面积的( )。
(3)将两个上底为5厘米,下底为7厘米,高为3厘米的梯形拼成一个平行四边形,这个平行四边形的底是
( )厘米,高是( )厘米。
相等
相等
一半
12
3
6.解决问题。
(1)“桂林山水甲天下”,漓江风光素有百里画廊之美称。为防止水患发生,在漓江上游修筑了防洪堤,其截面为等腰梯形。如下图,该梯形周长为51米,下底长比上底长的3倍还多3米,其腰长为多少米?
利用梯形的特征解决问题
[51-6-(6×3+3)]÷2=12(米)
答:其腰长为12米。
(2)用两个完全一样的直角梯形拼成一个长方形(如下图所示),直角梯形的上底是12厘米,下底是18厘米,高是8厘米,拼成的长方形的面积是多少平方厘米?
(12+18)×8=240(平方厘米)
答:拼成的长方形的面积是240平方厘米。
(3)王奶奶在自家院子中靠墙(墙足够长)围了一块梯形菜地(如下图所示)。梯形上底长2米,下底长3米,一条腰长4米,她要在菜地周围围上篱笆,10米长够吗?为什么?
2+3+4=9(米)
10>9
够了
7.数一数下面的图形中各有几个平行四边形和梯形。
平行四边形( )个 平行四边形( )个
梯形( )个 梯形( )个
运用组合法解决图形的问题
6
12
12
10
多边形的内角和
1.填一填。
(1)当多边形边数增加时,它的内角和会随着( ),如果多边形的边数增加一条,内角和就增加( )°,所以五边形的内角和比四边形多( )°。
(2)( )边形的内角和是六边形内角和的2倍;( )边形的内角和可以用7×180°来计算。
运用多边形内角和的
计算方法解决问题
增加
180
180
十
九
(3)一个多边形的边数增加4,则它的内角和增加( )°。
(4)一个多边形的内角和是1800°,则这个多边形是
( )边形。
(5)一个八边形,它每个角的度数都相等,则每个角的度数都是( )。
720
十二
135°
谢谢观赏
谢谢观赏
谢谢观赏
