人教版数学五年级下册4.5 最大公因数 课件(36张)
文档属性
| 名称 | 人教版数学五年级下册4.5 最大公因数 课件(36张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 09:30:25 | ||
图片预览







文档简介
(共36张PPT)
第5课时 最大公因数
1.理解公因数和最大公因数的意义。(重点)
2.掌握求两个数的最大公因数的方法,能正确找出
两个数的公因数及最大公因数。 (难点)
填一填。
○24÷6=4,( )和( )是( )的因数。
○36 的因数有( )。
6
24
4
1、2、3、4、6、9、12、18、36
因数的含义:
在整数除法中,如果商是整数而没有余数,那么被除数是除数的倍数,除数是被除数的因数。因数和倍数是相互依存的。
知识点 1
公因数和最大公因数的意义
1
8和12公有的因数是哪几个?公有的最大因数是多少?
我先分别找出8和12的因数。
8的因数: 1,2,4,8
12的因数:1,2,3,4,6,12
8和12公有的因数是1、2、4。
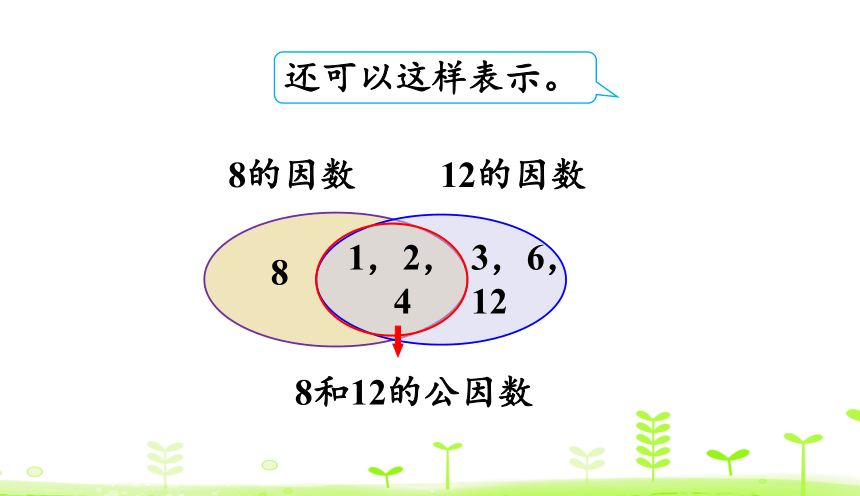
还可以这样表示。
8的因数
12的因数
8
3,6,12
1,2, 4
8和12的公因数
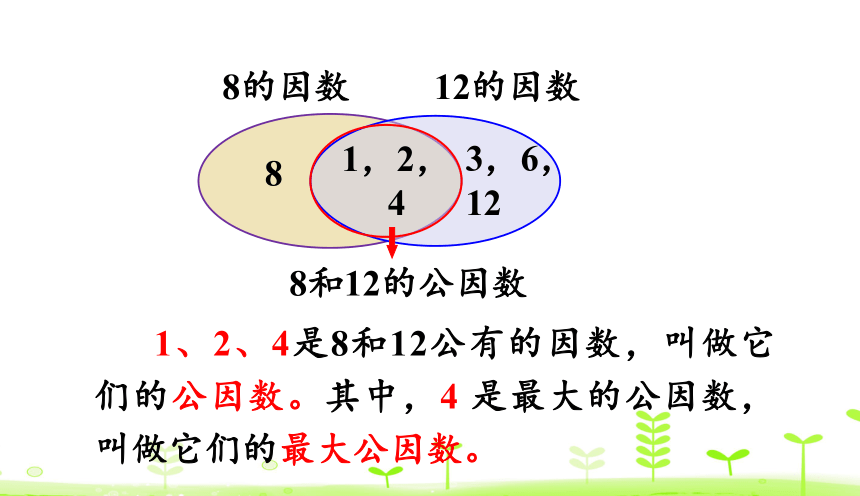
8的因数
12的因数
8
3,6,12
1,2, 4
8和12的公因数
1、2、4是8和12公有的因数,叫做它们的公因数。其中,4 是最大的公因数,叫做它们的最大公因数。
知识提炼
几个数公有的因数叫做这几个数的公因数,其中最大的那个公因数叫做这几个数的最大公因数。
(选自教材P61 T1)
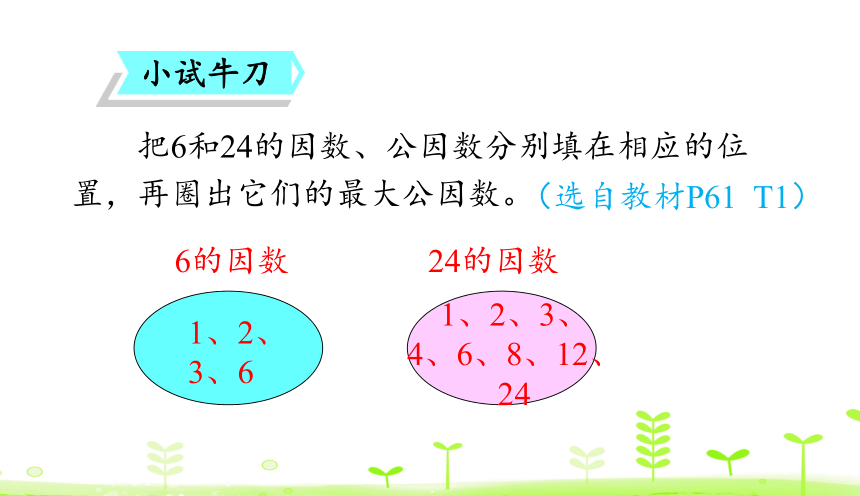
小试牛刀
把6和24的因数、公因数分别填在相应的位置,再圈出它们的最大公因数。
6的因数
24的因数
1、2、
3、6
1、2、3、
4、6、8、12、
24
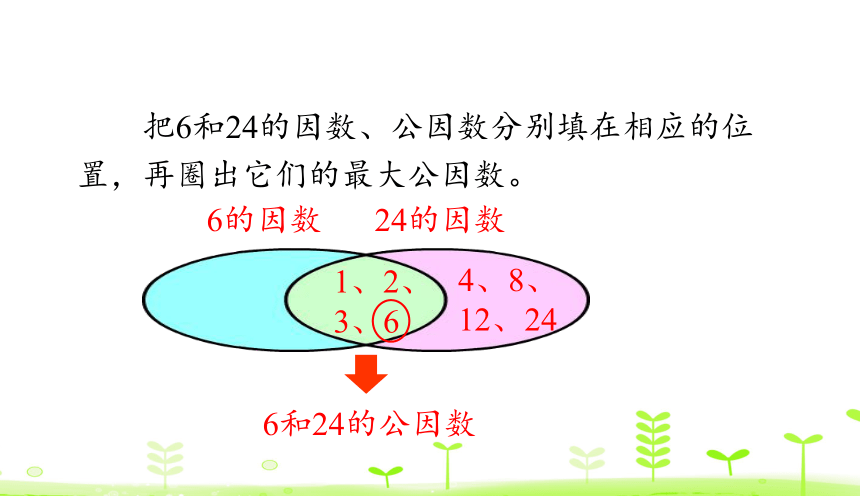
把6和24的因数、公因数分别填在相应的位置,再圈出它们的最大公因数。
6的因数
24的因数
1、2、
3、6
4、8、
12、24
6和24的公因数
知识点 2
求两个数最大公因数的方法(重点)
2
怎么求18和27的最大公因数?
方法一:列举法
18的因数:1,2,3,6,9,18。
27的因数:1,3,9,27。
它们的公因数1,3,9中,9最大。
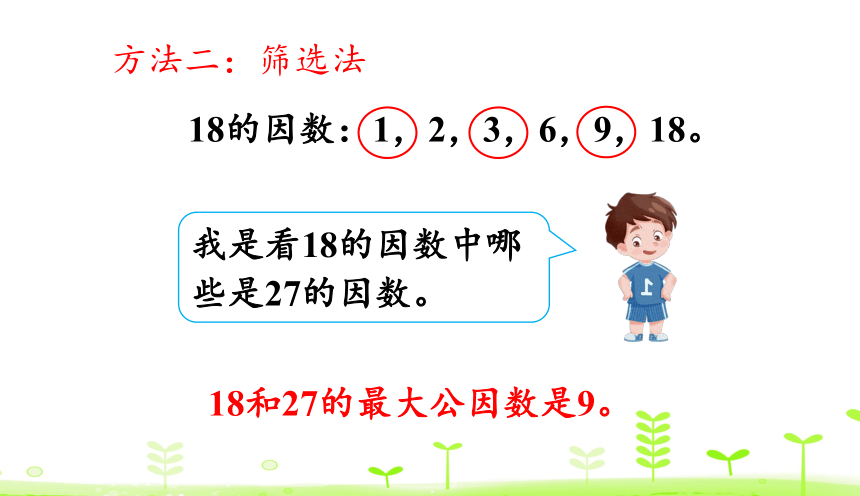
方法二:筛选法
18的因数:1,2,3,6,9,18。
我是看18的因数中哪些是27的因数。
18和27的最大公因数是9。
方法三:分解质因数法
18 和 27 的最大公因数是 3×3=9。
18 = 3 × 3 × 2
27 = 3 × 3 × 3
方法四:短除法
18 和 27 的最大公因数是 3×3=9。
18 27
3
6 9
3
2 3
8和12公有的因数是1、2、4。
8和12的最大公因数是4。
18和27公有的因数是1、3、9。
18和27的最大公因数是9。
观察一下,两个数的公因数和它们的最大公因数之间有什么关系?
两个数的公因数都是最大公因数的因数,两个数的最大公因数是公因数的倍数。
知识提炼
求两个数的最大公因数的方法:
(1)列举法。
(2)筛选法。
(3)分解质因数法。
(4)短除法。
小试牛刀
(选自教材P61 T3)
找出下列每组数的最大公因数。做完后你发现了什么?
4和8 12和36 1和7 8和9 12和35
4 和 8 的最大公因数是 4。
12 和 36 的最大公因数是 12。
1 和 7 的最大公因数是 1。
8 和 9 的最大公因数是 1。
12 和 35 的最大公因数是 1。
4 和 8:4 是 8 的因数,8 是 4 的倍数。
12 和 36:12 是 36 的因数,36 是 12 的倍数。
我发现:当两个数成倍数关系时,它们的最大公因数是较小数。
1 和 7:公因数只有 1。
8 和 9:公因数只有 1。
12 和 35:公因数只有 1。
我发现:当两个数是互质数时,它们的最大公因数是 1。
知识点 3
用求公因数的方法解决实际问题
3
如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
阅读与理解
你获得了哪些信息?
①要用正方形的地砖铺地。
②使用的地砖必须都是整块的,不能切割
开用半块的。
③正方形的边长必须是整分米数。
16dm
12dm
?dm
就是求选择边长是几分米的正方形恰好铺满这个长方形?
分析与解答
要使所用的正方形地砖都是整块的,地砖的边长必须既是16的因数,又是12的因数。
只要找出16和12的公因数和最大公因数,就知道正方形地砖的数量。
16的因数有:1、2、4、8、16;
12的因数有:1、2、3、4、6、12;
16和12的公因数有:1、2、4;
最大公因数是4。
所以可以选边长是1 dm、2 dm、4 dm的地砖,边长最大是4 dm。
可以动手画一画。
用边长1 dm的地砖铺,长边上用了整数块吗?宽边上呢?
回顾与反思
16 dm
12 dm
用边长 1 dm 的方砖,可以铺满,都是整块。
知识提炼
生活中的有些实际问题,可以转化为求两个数的公因数和最大公因数。
小试牛刀
(选自教材P63 T5)
有一张长方形纸,长 70 cm,宽 50 cm。如
果要剪成若干同样大小的正方形而没有剩余,
剪出的正方形的边长最大是几厘米?
剪出的正方形的边长最大是 10 cm。
两个合数的最大公因数可能是 1,如:14 和 15、27 和 32,它们的最大公因数都是 1。
√
×
例 判断:两个合数的最大公因数不可能是 1。
( )
解答错误
1.填空。
(1)10和15的公因数有 。
(2)14和49的公因数有 。
1, 5
1, 7
2.找出下面每组数的最大公因数。
(选自教材P63 T2)
6和9 15和12 42和54 30和45 99和36
5和9 34和17 16和48 15和16 13和78
3
3
6
15
9
1
17
16
1
13
3.男、女生分别站成若干排,要使每排的人数相同,
每排最多有多少人?这时男、女生分别有几排
(选自教材P63 T6)
48和36的最大公因数是12,
男生:48÷12=4(排)
女生:36÷12=3(排)
答:每排最多有12人,这时男、女生分别有4排、3排。
男生有48人,女生有36人
4.选出正确答案的序号填在横线上。
(选自教材P64 T9)
(1) 9和16的最大公因数是 。
A. 1 B. 3 C. 4 D. 9
(2)36和48的最大公因数是 。
A. 4 B. 6 C. 12 D. 36
(3)甲数是乙数的倍数,甲、乙两数的最大公因数
是 。
A. 1 B. 甲数 C. 乙数 D. 甲、乙两数的积
A
C
C
4.写出1,2,3,…,20各数与5的最大公因数,
你能发现什么规律?
规律:1~20中,5的倍数与5的最大公因数是5,其余的数与5的最大公因数是1。
1
1
1
1
5
1
1
1
1
5
1
1
1
1
5
1
1
1
1
5
这节课你们都学会了哪些知识?
1. 几个数公有的因数叫做这几个数的公因
数,其中最大的那个公因数叫做这几个
数的最大公因数。
2.求两个数的最大公因数的方法:
(1)列举法。
(2)筛选法。
(3)分解质因数法。
(4)短除法。
3.生活中的有些实际问题,可以转化为求两个
数的公因数和最大公因数。
作业1:完成教材相关练习题。
作业2:完成对应的练习题。
第5课时 最大公因数
1.理解公因数和最大公因数的意义。(重点)
2.掌握求两个数的最大公因数的方法,能正确找出
两个数的公因数及最大公因数。 (难点)
填一填。
○24÷6=4,( )和( )是( )的因数。
○36 的因数有( )。
6
24
4
1、2、3、4、6、9、12、18、36
因数的含义:
在整数除法中,如果商是整数而没有余数,那么被除数是除数的倍数,除数是被除数的因数。因数和倍数是相互依存的。
知识点 1
公因数和最大公因数的意义
1
8和12公有的因数是哪几个?公有的最大因数是多少?
我先分别找出8和12的因数。
8的因数: 1,2,4,8
12的因数:1,2,3,4,6,12
8和12公有的因数是1、2、4。
还可以这样表示。
8的因数
12的因数
8
3,6,12
1,2, 4
8和12的公因数
8的因数
12的因数
8
3,6,12
1,2, 4
8和12的公因数
1、2、4是8和12公有的因数,叫做它们的公因数。其中,4 是最大的公因数,叫做它们的最大公因数。
知识提炼
几个数公有的因数叫做这几个数的公因数,其中最大的那个公因数叫做这几个数的最大公因数。
(选自教材P61 T1)
小试牛刀
把6和24的因数、公因数分别填在相应的位置,再圈出它们的最大公因数。
6的因数
24的因数
1、2、
3、6
1、2、3、
4、6、8、12、
24
把6和24的因数、公因数分别填在相应的位置,再圈出它们的最大公因数。
6的因数
24的因数
1、2、
3、6
4、8、
12、24
6和24的公因数
知识点 2
求两个数最大公因数的方法(重点)
2
怎么求18和27的最大公因数?
方法一:列举法
18的因数:1,2,3,6,9,18。
27的因数:1,3,9,27。
它们的公因数1,3,9中,9最大。
方法二:筛选法
18的因数:1,2,3,6,9,18。
我是看18的因数中哪些是27的因数。
18和27的最大公因数是9。
方法三:分解质因数法
18 和 27 的最大公因数是 3×3=9。
18 = 3 × 3 × 2
27 = 3 × 3 × 3
方法四:短除法
18 和 27 的最大公因数是 3×3=9。
18 27
3
6 9
3
2 3
8和12公有的因数是1、2、4。
8和12的最大公因数是4。
18和27公有的因数是1、3、9。
18和27的最大公因数是9。
观察一下,两个数的公因数和它们的最大公因数之间有什么关系?
两个数的公因数都是最大公因数的因数,两个数的最大公因数是公因数的倍数。
知识提炼
求两个数的最大公因数的方法:
(1)列举法。
(2)筛选法。
(3)分解质因数法。
(4)短除法。
小试牛刀
(选自教材P61 T3)
找出下列每组数的最大公因数。做完后你发现了什么?
4和8 12和36 1和7 8和9 12和35
4 和 8 的最大公因数是 4。
12 和 36 的最大公因数是 12。
1 和 7 的最大公因数是 1。
8 和 9 的最大公因数是 1。
12 和 35 的最大公因数是 1。
4 和 8:4 是 8 的因数,8 是 4 的倍数。
12 和 36:12 是 36 的因数,36 是 12 的倍数。
我发现:当两个数成倍数关系时,它们的最大公因数是较小数。
1 和 7:公因数只有 1。
8 和 9:公因数只有 1。
12 和 35:公因数只有 1。
我发现:当两个数是互质数时,它们的最大公因数是 1。
知识点 3
用求公因数的方法解决实际问题
3
如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
阅读与理解
你获得了哪些信息?
①要用正方形的地砖铺地。
②使用的地砖必须都是整块的,不能切割
开用半块的。
③正方形的边长必须是整分米数。
16dm
12dm
?dm
就是求选择边长是几分米的正方形恰好铺满这个长方形?
分析与解答
要使所用的正方形地砖都是整块的,地砖的边长必须既是16的因数,又是12的因数。
只要找出16和12的公因数和最大公因数,就知道正方形地砖的数量。
16的因数有:1、2、4、8、16;
12的因数有:1、2、3、4、6、12;
16和12的公因数有:1、2、4;
最大公因数是4。
所以可以选边长是1 dm、2 dm、4 dm的地砖,边长最大是4 dm。
可以动手画一画。
用边长1 dm的地砖铺,长边上用了整数块吗?宽边上呢?
回顾与反思
16 dm
12 dm
用边长 1 dm 的方砖,可以铺满,都是整块。
知识提炼
生活中的有些实际问题,可以转化为求两个数的公因数和最大公因数。
小试牛刀
(选自教材P63 T5)
有一张长方形纸,长 70 cm,宽 50 cm。如
果要剪成若干同样大小的正方形而没有剩余,
剪出的正方形的边长最大是几厘米?
剪出的正方形的边长最大是 10 cm。
两个合数的最大公因数可能是 1,如:14 和 15、27 和 32,它们的最大公因数都是 1。
√
×
例 判断:两个合数的最大公因数不可能是 1。
( )
解答错误
1.填空。
(1)10和15的公因数有 。
(2)14和49的公因数有 。
1, 5
1, 7
2.找出下面每组数的最大公因数。
(选自教材P63 T2)
6和9 15和12 42和54 30和45 99和36
5和9 34和17 16和48 15和16 13和78
3
3
6
15
9
1
17
16
1
13
3.男、女生分别站成若干排,要使每排的人数相同,
每排最多有多少人?这时男、女生分别有几排
(选自教材P63 T6)
48和36的最大公因数是12,
男生:48÷12=4(排)
女生:36÷12=3(排)
答:每排最多有12人,这时男、女生分别有4排、3排。
男生有48人,女生有36人
4.选出正确答案的序号填在横线上。
(选自教材P64 T9)
(1) 9和16的最大公因数是 。
A. 1 B. 3 C. 4 D. 9
(2)36和48的最大公因数是 。
A. 4 B. 6 C. 12 D. 36
(3)甲数是乙数的倍数,甲、乙两数的最大公因数
是 。
A. 1 B. 甲数 C. 乙数 D. 甲、乙两数的积
A
C
C
4.写出1,2,3,…,20各数与5的最大公因数,
你能发现什么规律?
规律:1~20中,5的倍数与5的最大公因数是5,其余的数与5的最大公因数是1。
1
1
1
1
5
1
1
1
1
5
1
1
1
1
5
1
1
1
1
5
这节课你们都学会了哪些知识?
1. 几个数公有的因数叫做这几个数的公因
数,其中最大的那个公因数叫做这几个
数的最大公因数。
2.求两个数的最大公因数的方法:
(1)列举法。
(2)筛选法。
(3)分解质因数法。
(4)短除法。
3.生活中的有些实际问题,可以转化为求两个
数的公因数和最大公因数。
作业1:完成教材相关练习题。
作业2:完成对应的练习题。
