人教版数学五年级下册第9单元 总复习9.2 图形与几何 课件(23张)
文档属性
| 名称 | 人教版数学五年级下册第9单元 总复习9.2 图形与几何 课件(23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 11:34:56 | ||
图片预览








文档简介
(共23张PPT)
第2课时 图形与几何
1.能正确辨认从正面、左面、上面观察到的立体
图形的形状;进一步掌握图形的变换方法,掌
握对称的知识,对图形的旋转有更深入的认知。
(重点)
2.进一步掌握长方体和正方体的特征,能够根据
表面积和体积的含义正确地计算长方体、正方
体的表面积和体积。 (难点)
想一想,本学期学习了哪些知识,思考下列问题。
旋转的三要素是什么?
图形旋转的特征是怎样的?
长方体和正方体的特征是怎样的?
长方体和正方体的表面积的计算方法是怎样的?
体积计算公式是怎样的?
通过“观察物体(三)”,这个单元的学习,你们有什么感受和体会?
知识点1
观察物体
①根据从一个角度看到的物体形状,可以搭出不
同的立体图形;
②根据从三个方向观察到的平面图形,能确定立
体图形的形状。
下面 3 个几何体都是由棱长 1 cm 的小正方体摆成的。
①
②
③
(选自教材P116 T2)
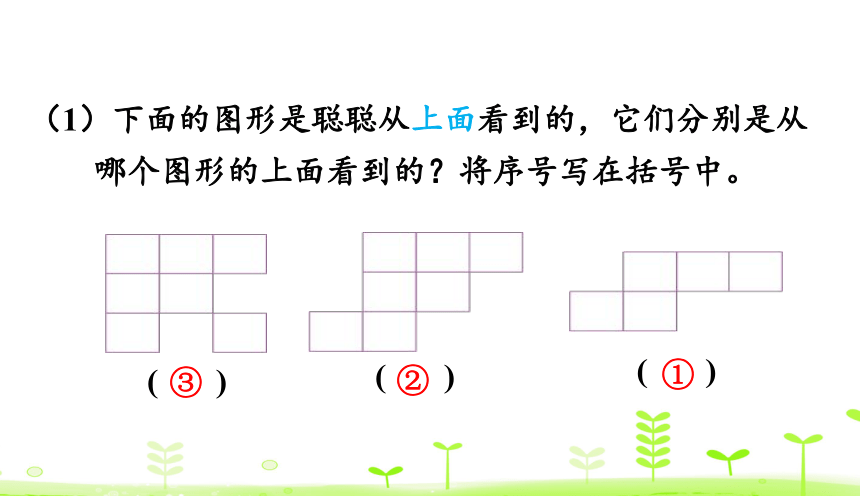
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个图形的上面看到的?将序号写在括号中。
( )
( )
( )
③
②
①
(2)①、②、③的体积分别是多少?
①的体积是6立方厘米;
②的体积是10立方厘米;
③的体积是11立方厘米。
①的体积是③的体积的几分之几?
6÷11=
6
11
(3)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
①还需要58个小立方体;
②还需要54个小立方体;
③还需要16个小立方体。
怎样想比较简便?
你还能提出其他数学问题并解答吗?
旋转的三要素是什么?
知识点2
图形的运动
旋转中心;
旋转角度;
旋转方向。
图形旋转的特征是怎样的?
图形旋转后,形状、大小都没有变化,只是位置发生变化。
(1)说一说左图可以通过怎样的变换得到右图。
绕鱼嘴顺时针(逆时针)旋转90°,连续旋转 4 次。
(选自教材P117 T3)
(2)右图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?红色部分比绿色部分多几分之几?
画出“风筝”旋转90°后的图形(只画出轮廓线)。
说一说你是怎样旋转并画出的。
(选自教材P120 T16)
长方体和正方体的表面积的计算方法是怎样的?
知识点3
长方体和正方体
长方体表面积 :(长×宽+长×高+宽×高)×2;
正方体的面积 :棱长 ×棱长 × 6。
长方体和正方体的体积公式是怎样的?
长方体的体积 =长 × 宽 × 高,字母表示为V=abh;
正方体的体积=V=a3
填写下表。
(选自教材P119 T11)
名 称 图形及条件 表 面 积 体 积
长方体 S= V=
正方体 S= V=
a
b
h
a
a
a
2(ab+ah+bh)
abh
a3
6a2
1.(1)举例说明 1 cm3、1 dm3、1 m3各有多大,1 L、1 mL的水大约有多少?
(选自教材P119 T12)
请同学们们举例说明。
(2)1 m3= dm3 700 dm3= m3
81 cm3= mL 1 L= dm3
2.3 dm3= cm3 560 mL= L
1000
0.7
81
1000
2300
0.56
13.一块长方形铁皮(如右图),从四个角落各切掉一个边长为 5 cm 的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积有多少?
表面积: 30×25-5×5×4=750-100
= 650(cm2)
容积: (30-5×2)×(25-5×2)×5
= 1500(cm3)=1500(mL)
(选自教材P120 T13)
14. 一只长方体的玻璃缸,长8dm、宽6dm、高4cm,水深2.8dm。如果投入一块棱长为4dm的正方体铁块(如右图),缸里的水溢出多少升?
8×6×2.8+4×4×4 -8×6×4
= 6.4( dm3 )= 6.4(L)
答:缸里的水溢出 6.4 L。
(选自教材P120 T14)
示例:
15.用 4 个 摆一摆。
(1)如果从左侧看到的形状是 ,这 4 个小正方体可能是怎样摆放的?
(选自教材P120 T15)
请同学们和同桌一起做一做。
(2)请你再给出从另一个方向看到的形状,让同桌猜一猜 4 个 是怎样摆放的。
作业1:完成教材相关练习题。
作业2:完成对应的练习题。
第2课时 图形与几何
1.能正确辨认从正面、左面、上面观察到的立体
图形的形状;进一步掌握图形的变换方法,掌
握对称的知识,对图形的旋转有更深入的认知。
(重点)
2.进一步掌握长方体和正方体的特征,能够根据
表面积和体积的含义正确地计算长方体、正方
体的表面积和体积。 (难点)
想一想,本学期学习了哪些知识,思考下列问题。
旋转的三要素是什么?
图形旋转的特征是怎样的?
长方体和正方体的特征是怎样的?
长方体和正方体的表面积的计算方法是怎样的?
体积计算公式是怎样的?
通过“观察物体(三)”,这个单元的学习,你们有什么感受和体会?
知识点1
观察物体
①根据从一个角度看到的物体形状,可以搭出不
同的立体图形;
②根据从三个方向观察到的平面图形,能确定立
体图形的形状。
下面 3 个几何体都是由棱长 1 cm 的小正方体摆成的。
①
②
③
(选自教材P116 T2)
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个图形的上面看到的?将序号写在括号中。
( )
( )
( )
③
②
①
(2)①、②、③的体积分别是多少?
①的体积是6立方厘米;
②的体积是10立方厘米;
③的体积是11立方厘米。
①的体积是③的体积的几分之几?
6÷11=
6
11
(3)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
①还需要58个小立方体;
②还需要54个小立方体;
③还需要16个小立方体。
怎样想比较简便?
你还能提出其他数学问题并解答吗?
旋转的三要素是什么?
知识点2
图形的运动
旋转中心;
旋转角度;
旋转方向。
图形旋转的特征是怎样的?
图形旋转后,形状、大小都没有变化,只是位置发生变化。
(1)说一说左图可以通过怎样的变换得到右图。
绕鱼嘴顺时针(逆时针)旋转90°,连续旋转 4 次。
(选自教材P117 T3)
(2)右图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?红色部分比绿色部分多几分之几?
画出“风筝”旋转90°后的图形(只画出轮廓线)。
说一说你是怎样旋转并画出的。
(选自教材P120 T16)
长方体和正方体的表面积的计算方法是怎样的?
知识点3
长方体和正方体
长方体表面积 :(长×宽+长×高+宽×高)×2;
正方体的面积 :棱长 ×棱长 × 6。
长方体和正方体的体积公式是怎样的?
长方体的体积 =长 × 宽 × 高,字母表示为V=abh;
正方体的体积=V=a3
填写下表。
(选自教材P119 T11)
名 称 图形及条件 表 面 积 体 积
长方体 S= V=
正方体 S= V=
a
b
h
a
a
a
2(ab+ah+bh)
abh
a3
6a2
1.(1)举例说明 1 cm3、1 dm3、1 m3各有多大,1 L、1 mL的水大约有多少?
(选自教材P119 T12)
请同学们们举例说明。
(2)1 m3= dm3 700 dm3= m3
81 cm3= mL 1 L= dm3
2.3 dm3= cm3 560 mL= L
1000
0.7
81
1000
2300
0.56
13.一块长方形铁皮(如右图),从四个角落各切掉一个边长为 5 cm 的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积有多少?
表面积: 30×25-5×5×4=750-100
= 650(cm2)
容积: (30-5×2)×(25-5×2)×5
= 1500(cm3)=1500(mL)
(选自教材P120 T13)
14. 一只长方体的玻璃缸,长8dm、宽6dm、高4cm,水深2.8dm。如果投入一块棱长为4dm的正方体铁块(如右图),缸里的水溢出多少升?
8×6×2.8+4×4×4 -8×6×4
= 6.4( dm3 )= 6.4(L)
答:缸里的水溢出 6.4 L。
(选自教材P120 T14)
示例:
15.用 4 个 摆一摆。
(1)如果从左侧看到的形状是 ,这 4 个小正方体可能是怎样摆放的?
(选自教材P120 T15)
请同学们和同桌一起做一做。
(2)请你再给出从另一个方向看到的形状,让同桌猜一猜 4 个 是怎样摆放的。
作业1:完成教材相关练习题。
作业2:完成对应的练习题。
