人教版高中数学必修三3.1.3 概率的基本性质(共28张PPT)
文档属性
| 名称 | 人教版高中数学必修三3.1.3 概率的基本性质(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
概率的基本性质
在一次有关三国演义的知识竞赛中,三个臭皮匠ABC能答对题目的概率P(A)=1/3 P(B)=1/4 P(C)=1/5 (他们能答对的题目不重复),诸葛亮D能答对题目的概率P(D)=2/3 ,如果将三个臭皮匠组成一组与诸葛亮D比赛,答对题目多者为胜方,则哪方胜?
俗话说“三个臭皮匠顶个诸葛亮” 能顶上吗?
创设问题情境
【学习目标】
1.通过类比集合与集合的关系与运算,学习事件的包含、相等关系,并事件,交事件, 以及互斥事件, 对立事件的概念;
2.能叙述互斥事件与对立事件的区别与联系
3. 说出概率的基本性质;会使用互斥事件、对立事件的概率性质求概率。
在掷骰子的试验中,我们可以定义许多事件,如:
C1 ={ 出现 1 点 }; C2 ={出现 2 点};
C3 ={ 出现 3 点 }; C4 ={ 出现 4 点 };
C5 ={出现 5 点}; C6 ={ 出现 6 点 };
D1 ={ 出现的点数不大于 1 } D2 ={ 出现的点数大于 3 };
D3 ={ 出现的点数小于 5 };E ={ 出现的点数小于 7 };
F ={ 出现的点数大于 6 }; G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 };……
类比集合与集合的关系、运算你能发现事件 之间的关系和运算吗?
1. 上述事件中有必然事件或不可能事件吗?有的话,哪些是?
2. 若事件 C1 发生,则还有哪些事件也一定会发生?反过来可以么?
3. 如果事件C2发生或C4发生或C6发生,就意味着哪个事件发生 ?
4. 如果事件D2与事件D3同时发生 ,就意味着哪个事件发生?
5. 事件 C1 和事件 C2 有可能同时发生么?
6. 事件 G 和事件 H 是否能同时发生,是否一定有一个会发生?它们两个事件有何关系?
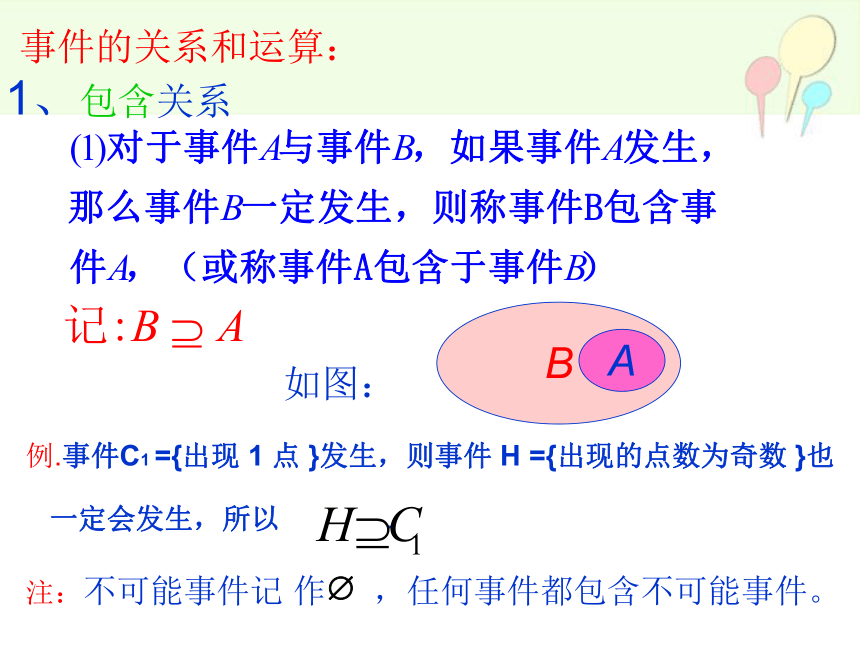
事件的关系和运算:
B
A
如图:
1、包含关系
事件的关系和运算:
2、相等关系
B
A
如图:
例.事件 C1 ={ 出现1 点 }发生,则事件 D1 ={出现的点数不大于 1 }就一定会发生,反过来也一样,所以C1=D1。
党委副书记、镇长民主生活会个人分析检查材料及整改措施
根据区纪委、区委组织部和镇党委的统一部署,紧紧围绕“贯彻落实切实加强领导干部作风建设”这一主题,在认真学习十七届四、五全会精神和胡锦涛同志在纪委第四次、五次全会上的讲话及全会工作报告的基础上,在广泛征求群众意见,认真查摆廉洁自律、工作作风方面存在的问题,深刻剖析问题存在的主客观原因,进一步加深了对“党风关系党的生死存亡”、“坚决惩治和有效预防腐败,是党必须始终抓好的重大政治任务”的理解和认识,进一步理顺了加快发展的思路和举措;增强了信心和决心。现就存在的问题剖析如下:
一、存在问题
1、学习不够深入。主要是思想上存在重工作轻学习的现象,主观上以工作繁忙为借口,不能经常性的主动学习。在学习过程,重表面,轻内涵,没有从深层次上系统地学习、理解、领会党员领导干部廉洁从政的重要意义。理论学习与工作实际结合的不够充分,尚未把党风廉政建设与政务公开、村务公开,与推动工作很好结合起来。在自身综合素质的提高上也还存在一定的差距,不能虚心的学习其它班子成员和基层群众身上的优点和长处,学习能力有待于进一步提高。
2、思想不够解放。受个人性格、惯性思维的
事件的关系和运算:
3、并事件(和事件)
B
A
如图:
事件的关系和运算:
(4)交事件(积事件)
B
A
如图:
事件的关系和运算:
5、互斥事件
A
B
如图:
例.因为事件 C1 ={出现 1 点} 与事件C2 ={出现 2 点}
不可能同时发 生,故这两个事件互斥。
事件的关系和运算:
6、互为对立事件
如图:
例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数}即为互为对立事件。
事件的关系和运算
事件 运算
事件 关系
1.包含关系
2.等价关系
3.事件的并 (或和)
4.事件的交 (或积)
5.事件的互斥 (或互不相容)
6.对立事件
思考:你能说说互斥事件和对立事件的区别吗?
错
对
对
例1. 从一堆产品(其中正品和次品都多于 2件)中一次任取 2件,观察正品件数和次品件数,判断下列每对事件是不是互斥事件,若是,再判断它们是不是对立事件:
(1)恰好有 1 件次品和恰好有 2 件次品;
(2)至少有 1 件次品和全是次品;
(3)至少有 1 件正品和至少有 1件次品;
(4)至少有 1 件次品和全是正品。
A:正正
B:一正一次
C:次次
互斥不对立
不互斥不对立
不互斥不对立
互斥且对立
探究二 应用举例:
探究活动三:概率的性质(从上面实验的频数和频率的角度来分析)
(1)必然事件的概率是多少?
(2)不可能事件的概率是多少?
(3)概率的取值范围是多少?
(4)互斥事件的概率应怎样计算?
(5)对立事件的概率应怎样计算?
二:概率的基本性质
1) 必然事件B一定发生, 则 P(B)=1
2) 不可能事件C一定不发生, 则P(C)=0
3) 概率的取值范围为0≤P(A)≤1
2.概率的加法公式
当事件A与B互斥时, A∪B发生的概率为P(A∪B)=P(A)+P(B)
P(C)=P(A∪B)=P(A)+P(B)=1/6+1/6=1/3
即两个事件彼此互斥时,和事件的概率等于
各自事件的概率之和
引申
如果事件A1,A2,…An 彼此互斥,
P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An)
即彼此互斥事件的的概率等于概率的和。
如果事件不互斥,上述公式就不能使用!
另外,“正难则反”是解决问题的一种很好的方法,应掌握.
3. 对立事件有一个发生的概率
当事件A与B对立时,则P(A∩B)=0,P(A∪B)= 1, A发生的概率为P(A)=1- P(B)
P(G) = 1-P(H)=1- 1/2 = 1/2
探究四:典题解析
例2 : 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方块(事件B)的概率是 ,问:(1)取到红色牌(事件C)的概率是多少?(2)取到黑色牌(事件D)的概率是多少?
解:(1)因为C=A∪B,且A与B不会同时发生,所以事件A与事件B互斥,根据概率的加法公式得P(C)=P(A)+P(B)= 。
(2)事件C与事件D互斥,且C∪D为必然事件,因此事件C与事件D是对立事件,P(D)=1-P(C)= 。
在一次有关三国演义的知识竞赛中,三个臭皮匠ABC能答对题目的概率P(A)=1/3 P(B)=1/4 P(C)=1/5 (他们能答对的题目不重复),诸葛亮D能答对题目的概率P(D)=2/3 ,如果将三个臭皮匠组成一组与诸葛亮D比赛,答对题目多者为胜方,则哪方胜?
俗话说“三个臭皮匠顶个诸葛亮” 能顶上吗?
应用提高
解:如果三个臭皮匠A、B、C能答对的题目彼此互斥(他们能答对的题目不重复),则P(A+B+C)
=P(A)+P(B)+P(C)
=
故三个臭皮匠方为胜方,即三个臭皮匠能顶上一个诸葛亮;如果三个臭皮匠A、B、C能答对的题目不互斥,则三个臭皮匠未必能顶上一个诸葛亮.
课堂小结
通过这一节学习,你有哪些收获? (比如知识、方法、能力、兴趣等)
概率的基本性质
事件的关系与运算
包含关系
概率的基本性质
相等关系
并(和)事件
交(积)事件
互斥事件
对立事件
必然事件的概率为1
不可能事件的概率为0
互斥事件概率的加法公式
对立事件计算公式
0≤P(A) ≤1
小结
【检测】
【课堂检测】
1、下列说法中正确的是( D )
A.事件A、B中至少有一个发生的概率一定比A、 B中恰有一个发生的概率大
B.事件A、B同时发生的概率一定比事件A、B恰有一个发生的概率小
C.互斥事件一定是对立事件,对立事件不一定是互斥事件
D.互斥事件不一定是对立事件,对立事件一定是互斥事件
2. 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环
事件B:命中环数为10环;
事件C:命中环数小于6环;
事件D:命中环数为6、7、 8 、9、10环.
分析:要判断所给事件是对立还是互斥,首先将两个概念的联系与区别弄清楚,互斥事件是指不可能同时发生的两事件,而对立事件是建立在互斥事件的基础上,两个事件中一个不发生,另一个必发生。
解:A与C互斥,B与C互斥,C与D互斥,C与D是对立事件.
3.甲,乙两人下棋,若和棋的概率是0.5,乙获胜的概率是0.3
求:(1)甲获胜的概率;(2)甲不输的概率。
解:(1)“甲获胜”是“和棋或乙获胜”的对立事件,因为“和棋”与“乙获胜”是互斥事件,所以
甲获胜的概率为:1-(0.5+0.3)=0.2
(2)设事件A={甲不输},B={和棋},C={甲获胜}
则A=B∪C,因为B,C是互斥事件,所以
P(A)=P(B)+P(C)=0.5+0.2=0.7
概率的基本性质
在一次有关三国演义的知识竞赛中,三个臭皮匠ABC能答对题目的概率P(A)=1/3 P(B)=1/4 P(C)=1/5 (他们能答对的题目不重复),诸葛亮D能答对题目的概率P(D)=2/3 ,如果将三个臭皮匠组成一组与诸葛亮D比赛,答对题目多者为胜方,则哪方胜?
俗话说“三个臭皮匠顶个诸葛亮” 能顶上吗?
创设问题情境
【学习目标】
1.通过类比集合与集合的关系与运算,学习事件的包含、相等关系,并事件,交事件, 以及互斥事件, 对立事件的概念;
2.能叙述互斥事件与对立事件的区别与联系
3. 说出概率的基本性质;会使用互斥事件、对立事件的概率性质求概率。
在掷骰子的试验中,我们可以定义许多事件,如:
C1 ={ 出现 1 点 }; C2 ={出现 2 点};
C3 ={ 出现 3 点 }; C4 ={ 出现 4 点 };
C5 ={出现 5 点}; C6 ={ 出现 6 点 };
D1 ={ 出现的点数不大于 1 } D2 ={ 出现的点数大于 3 };
D3 ={ 出现的点数小于 5 };E ={ 出现的点数小于 7 };
F ={ 出现的点数大于 6 }; G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 };……
类比集合与集合的关系、运算你能发现事件 之间的关系和运算吗?
1. 上述事件中有必然事件或不可能事件吗?有的话,哪些是?
2. 若事件 C1 发生,则还有哪些事件也一定会发生?反过来可以么?
3. 如果事件C2发生或C4发生或C6发生,就意味着哪个事件发生 ?
4. 如果事件D2与事件D3同时发生 ,就意味着哪个事件发生?
5. 事件 C1 和事件 C2 有可能同时发生么?
6. 事件 G 和事件 H 是否能同时发生,是否一定有一个会发生?它们两个事件有何关系?
事件的关系和运算:
B
A
如图:
1、包含关系
事件的关系和运算:
2、相等关系
B
A
如图:
例.事件 C1 ={ 出现1 点 }发生,则事件 D1 ={出现的点数不大于 1 }就一定会发生,反过来也一样,所以C1=D1。
党委副书记、镇长民主生活会个人分析检查材料及整改措施
根据区纪委、区委组织部和镇党委的统一部署,紧紧围绕“贯彻落实切实加强领导干部作风建设”这一主题,在认真学习十七届四、五全会精神和胡锦涛同志在纪委第四次、五次全会上的讲话及全会工作报告的基础上,在广泛征求群众意见,认真查摆廉洁自律、工作作风方面存在的问题,深刻剖析问题存在的主客观原因,进一步加深了对“党风关系党的生死存亡”、“坚决惩治和有效预防腐败,是党必须始终抓好的重大政治任务”的理解和认识,进一步理顺了加快发展的思路和举措;增强了信心和决心。现就存在的问题剖析如下:
一、存在问题
1、学习不够深入。主要是思想上存在重工作轻学习的现象,主观上以工作繁忙为借口,不能经常性的主动学习。在学习过程,重表面,轻内涵,没有从深层次上系统地学习、理解、领会党员领导干部廉洁从政的重要意义。理论学习与工作实际结合的不够充分,尚未把党风廉政建设与政务公开、村务公开,与推动工作很好结合起来。在自身综合素质的提高上也还存在一定的差距,不能虚心的学习其它班子成员和基层群众身上的优点和长处,学习能力有待于进一步提高。
2、思想不够解放。受个人性格、惯性思维的
事件的关系和运算:
3、并事件(和事件)
B
A
如图:
事件的关系和运算:
(4)交事件(积事件)
B
A
如图:
事件的关系和运算:
5、互斥事件
A
B
如图:
例.因为事件 C1 ={出现 1 点} 与事件C2 ={出现 2 点}
不可能同时发 生,故这两个事件互斥。
事件的关系和运算:
6、互为对立事件
如图:
例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数}即为互为对立事件。
事件的关系和运算
事件 运算
事件 关系
1.包含关系
2.等价关系
3.事件的并 (或和)
4.事件的交 (或积)
5.事件的互斥 (或互不相容)
6.对立事件
思考:你能说说互斥事件和对立事件的区别吗?
错
对
对
例1. 从一堆产品(其中正品和次品都多于 2件)中一次任取 2件,观察正品件数和次品件数,判断下列每对事件是不是互斥事件,若是,再判断它们是不是对立事件:
(1)恰好有 1 件次品和恰好有 2 件次品;
(2)至少有 1 件次品和全是次品;
(3)至少有 1 件正品和至少有 1件次品;
(4)至少有 1 件次品和全是正品。
A:正正
B:一正一次
C:次次
互斥不对立
不互斥不对立
不互斥不对立
互斥且对立
探究二 应用举例:
探究活动三:概率的性质(从上面实验的频数和频率的角度来分析)
(1)必然事件的概率是多少?
(2)不可能事件的概率是多少?
(3)概率的取值范围是多少?
(4)互斥事件的概率应怎样计算?
(5)对立事件的概率应怎样计算?
二:概率的基本性质
1) 必然事件B一定发生, 则 P(B)=1
2) 不可能事件C一定不发生, 则P(C)=0
3) 概率的取值范围为0≤P(A)≤1
2.概率的加法公式
当事件A与B互斥时, A∪B发生的概率为P(A∪B)=P(A)+P(B)
P(C)=P(A∪B)=P(A)+P(B)=1/6+1/6=1/3
即两个事件彼此互斥时,和事件的概率等于
各自事件的概率之和
引申
如果事件A1,A2,…An 彼此互斥,
P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An)
即彼此互斥事件的的概率等于概率的和。
如果事件不互斥,上述公式就不能使用!
另外,“正难则反”是解决问题的一种很好的方法,应掌握.
3. 对立事件有一个发生的概率
当事件A与B对立时,则P(A∩B)=0,P(A∪B)= 1, A发生的概率为P(A)=1- P(B)
P(G) = 1-P(H)=1- 1/2 = 1/2
探究四:典题解析
例2 : 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方块(事件B)的概率是 ,问:(1)取到红色牌(事件C)的概率是多少?(2)取到黑色牌(事件D)的概率是多少?
解:(1)因为C=A∪B,且A与B不会同时发生,所以事件A与事件B互斥,根据概率的加法公式得P(C)=P(A)+P(B)= 。
(2)事件C与事件D互斥,且C∪D为必然事件,因此事件C与事件D是对立事件,P(D)=1-P(C)= 。
在一次有关三国演义的知识竞赛中,三个臭皮匠ABC能答对题目的概率P(A)=1/3 P(B)=1/4 P(C)=1/5 (他们能答对的题目不重复),诸葛亮D能答对题目的概率P(D)=2/3 ,如果将三个臭皮匠组成一组与诸葛亮D比赛,答对题目多者为胜方,则哪方胜?
俗话说“三个臭皮匠顶个诸葛亮” 能顶上吗?
应用提高
解:如果三个臭皮匠A、B、C能答对的题目彼此互斥(他们能答对的题目不重复),则P(A+B+C)
=P(A)+P(B)+P(C)
=
故三个臭皮匠方为胜方,即三个臭皮匠能顶上一个诸葛亮;如果三个臭皮匠A、B、C能答对的题目不互斥,则三个臭皮匠未必能顶上一个诸葛亮.
课堂小结
通过这一节学习,你有哪些收获? (比如知识、方法、能力、兴趣等)
概率的基本性质
事件的关系与运算
包含关系
概率的基本性质
相等关系
并(和)事件
交(积)事件
互斥事件
对立事件
必然事件的概率为1
不可能事件的概率为0
互斥事件概率的加法公式
对立事件计算公式
0≤P(A) ≤1
小结
【检测】
【课堂检测】
1、下列说法中正确的是( D )
A.事件A、B中至少有一个发生的概率一定比A、 B中恰有一个发生的概率大
B.事件A、B同时发生的概率一定比事件A、B恰有一个发生的概率小
C.互斥事件一定是对立事件,对立事件不一定是互斥事件
D.互斥事件不一定是对立事件,对立事件一定是互斥事件
2. 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环
事件B:命中环数为10环;
事件C:命中环数小于6环;
事件D:命中环数为6、7、 8 、9、10环.
分析:要判断所给事件是对立还是互斥,首先将两个概念的联系与区别弄清楚,互斥事件是指不可能同时发生的两事件,而对立事件是建立在互斥事件的基础上,两个事件中一个不发生,另一个必发生。
解:A与C互斥,B与C互斥,C与D互斥,C与D是对立事件.
3.甲,乙两人下棋,若和棋的概率是0.5,乙获胜的概率是0.3
求:(1)甲获胜的概率;(2)甲不输的概率。
解:(1)“甲获胜”是“和棋或乙获胜”的对立事件,因为“和棋”与“乙获胜”是互斥事件,所以
甲获胜的概率为:1-(0.5+0.3)=0.2
(2)设事件A={甲不输},B={和棋},C={甲获胜}
则A=B∪C,因为B,C是互斥事件,所以
P(A)=P(B)+P(C)=0.5+0.2=0.7
