四年级下册数学课件9.1 数的世界整理与复习苏教版 (共18张PPT)
文档属性
| 名称 | 四年级下册数学课件9.1 数的世界整理与复习苏教版 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 691.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
二、认识多位数
1、数位顺序表(数位、计数单位、十进制)
2、多位数读法:
从高位读起,亿级、万级的读法
跟个级的读法相同,在后面加读“亿万”
没级末尾的0不读,其他数位有一个0,或者连续几个0,都只读一个零
3、多位数写法:
从高位写起,有几个亿,就在亿级写几,有几个万,就在万级写几。哪一位上一个数也没有,就在哪一位上写0.
4、改写
①改写的数都是整万、整亿的
②改写是直等
③“万”顶4个0,“亿”顶8个0
如:400000=40万
5、比较多位数大小
①先比
②再比
6、求近似数
①不是整亿、整万
②约等号
③四舍五入
④精确到万位,要看哪一位?
如精确到百万位:45963010
1□7584≈10万,□内最大填。
一个数约等于4万,则这个数最大是( )
练习题:
1、6872200是由( )个万和( )个一组成。
2、13054897是( )位数,它的最高位是( )位。
3、三亿零五十六万 写作:
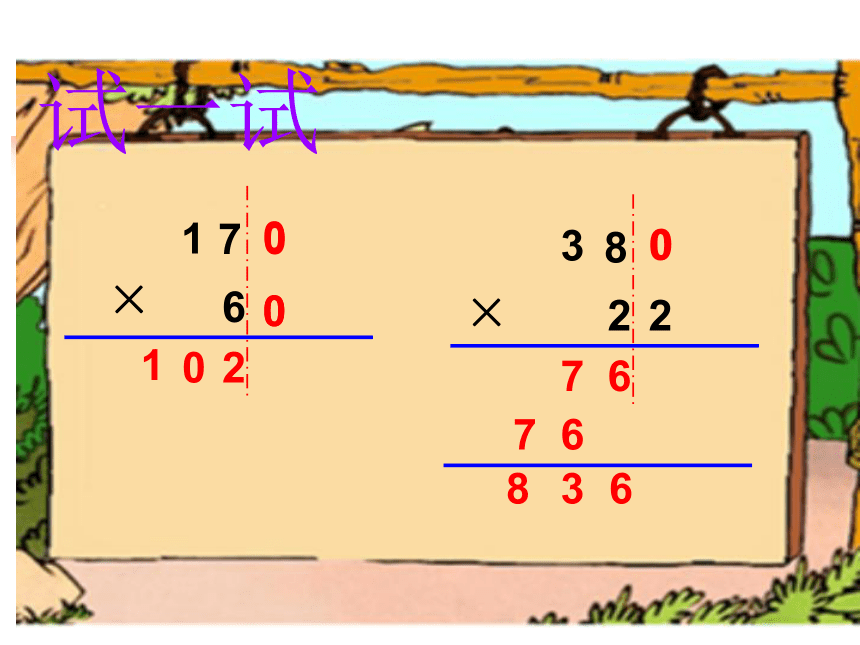
三、三位数乘两位数(积可能是几位数)
一般的乘法:460×23(竖式) 末尾有0的乘法:40×240
1、公式(及其变化公式):
总价= 路程=
2、积的变化规律:
×
0
2
0
7
0
1
1
0
0
×
0
6
7
8
0
3
6
7
6
3
8
试一试
根据每组第一题的算式,直接写出后两题的得数.
24×3=72
24×30=
24×300=
7×15=105
7×150=
7×1500=
720
7200
1050
10500
四、计算器
开机键、清除键、数字键、运算符号键
六、运算律
加法2个:
a+b=b+a
a+b+c= a+(b+c)
乘法3个:
a×b=b×a
a×b×c= a× (b×c)
(a+b)×c= a×c+b×c
六、运算律
简便算法:除了以上5个,还有
a-b-c=a-(b+c)
a÷b÷c= a÷ (b×c)
遇到混合运算,不会用简便算法的,用常规的运算顺序做
加法交换律:
我们学过哪些整数运算的运算律?用字母表示出来。
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
除法的性质:
减法的性质:
乘法分配律:
乘法结合律:
乘法交换律:
加法结合律:
五个定律
两个性质
(a-b)×c=a×c-b×c
下面的计算分别应用了什么运算律?
86+35=35+86
( )
72+57+43=72+(57+43)
( )
76×40×25=76×(40×25)
( )
125×67×8=125×8×67
( )
加法交换律
加法结合律
乘法结合律
乘法交换律
下面的计算分别应用了什么运算律?
46×37+37×54= 37×(46+54 )
( )
4×8×25×125=4×25×(125×8)
( )
437-161-39 =437-(161+39)
( )
12700÷25÷4=12700÷(25×4)
( )
乘法分配律
乘法交换律和乘法结合律
减法的性质
除法的性质
计算
① 46+32+54 ②546+785-146
③7+39+43+61 ④25×49×4
=(46+54)+32
=(546-146)+785
=(7+43)+(39+61)
=(25×4)×49
= 100+32
= 400+785
= 1185
= 50+100
= 150
=100×49
=132
=4900
计算
⑤8×(36×125) ⑥8×4×125×25
⑦27×48+27×52 ⑧905×99+905
=(8×125)×36
=(8×125)×(4×25)
=27×(48+52)
=905×(99+1)
= 1000×36
=36000
= 1000×100
= 27×100
=905×100
=90500
=100000
=2700
计算
⑨437 - + 63 - ⑩ 1047-568-132
=(437+63)-(15+ 85 )
= 1047-(568+132)
= 500-100
= 1047-700
=400
=347
计算
(11) 4800÷25÷4
= 4800÷(25×4)
= 4800÷100
=48
二、认识多位数
1、数位顺序表(数位、计数单位、十进制)
2、多位数读法:
从高位读起,亿级、万级的读法
跟个级的读法相同,在后面加读“亿万”
没级末尾的0不读,其他数位有一个0,或者连续几个0,都只读一个零
3、多位数写法:
从高位写起,有几个亿,就在亿级写几,有几个万,就在万级写几。哪一位上一个数也没有,就在哪一位上写0.
4、改写
①改写的数都是整万、整亿的
②改写是直等
③“万”顶4个0,“亿”顶8个0
如:400000=40万
5、比较多位数大小
①先比
②再比
6、求近似数
①不是整亿、整万
②约等号
③四舍五入
④精确到万位,要看哪一位?
如精确到百万位:45963010
1□7584≈10万,□内最大填。
一个数约等于4万,则这个数最大是( )
练习题:
1、6872200是由( )个万和( )个一组成。
2、13054897是( )位数,它的最高位是( )位。
3、三亿零五十六万 写作:
三、三位数乘两位数(积可能是几位数)
一般的乘法:460×23(竖式) 末尾有0的乘法:40×240
1、公式(及其变化公式):
总价= 路程=
2、积的变化规律:
×
0
2
0
7
0
1
1
0
0
×
0
6
7
8
0
3
6
7
6
3
8
试一试
根据每组第一题的算式,直接写出后两题的得数.
24×3=72
24×30=
24×300=
7×15=105
7×150=
7×1500=
720
7200
1050
10500
四、计算器
开机键、清除键、数字键、运算符号键
六、运算律
加法2个:
a+b=b+a
a+b+c= a+(b+c)
乘法3个:
a×b=b×a
a×b×c= a× (b×c)
(a+b)×c= a×c+b×c
六、运算律
简便算法:除了以上5个,还有
a-b-c=a-(b+c)
a÷b÷c= a÷ (b×c)
遇到混合运算,不会用简便算法的,用常规的运算顺序做
加法交换律:
我们学过哪些整数运算的运算律?用字母表示出来。
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
除法的性质:
减法的性质:
乘法分配律:
乘法结合律:
乘法交换律:
加法结合律:
五个定律
两个性质
(a-b)×c=a×c-b×c
下面的计算分别应用了什么运算律?
86+35=35+86
( )
72+57+43=72+(57+43)
( )
76×40×25=76×(40×25)
( )
125×67×8=125×8×67
( )
加法交换律
加法结合律
乘法结合律
乘法交换律
下面的计算分别应用了什么运算律?
46×37+37×54= 37×(46+54 )
( )
4×8×25×125=4×25×(125×8)
( )
437-161-39 =437-(161+39)
( )
12700÷25÷4=12700÷(25×4)
( )
乘法分配律
乘法交换律和乘法结合律
减法的性质
除法的性质
计算
① 46+32+54 ②546+785-146
③7+39+43+61 ④25×49×4
=(46+54)+32
=(546-146)+785
=(7+43)+(39+61)
=(25×4)×49
= 100+32
= 400+785
= 1185
= 50+100
= 150
=100×49
=132
=4900
计算
⑤8×(36×125) ⑥8×4×125×25
⑦27×48+27×52 ⑧905×99+905
=(8×125)×36
=(8×125)×(4×25)
=27×(48+52)
=905×(99+1)
= 1000×36
=36000
= 1000×100
= 27×100
=905×100
=90500
=100000
=2700
计算
⑨437 - + 63 - ⑩ 1047-568-132
=(437+63)-(15+ 85 )
= 1047-(568+132)
= 500-100
= 1047-700
=400
=347
计算
(11) 4800÷25÷4
= 4800÷(25×4)
= 4800÷100
=48
