北师大版数学八年级下册:4.1 因式分解 课件(共18张PPT)
文档属性
| 名称 | 北师大版数学八年级下册:4.1 因式分解 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
一、用简便方法计算:(先说结果后说方法)
(1) =
(2)-2.67× 132+25×2.67+7×2.67=
(3)99 –1= .
7
9
× 13 – × 6+ × 2
7
9
7
9
2
7
-267
9800
=(13-6+2)X =9X
7
9
=2.67x(-132+25+7)=2.67X(-100)
=(99+1)(99-1)=100x98
7
9
二、99 –99能被100整除吗?你是怎样想的?
3
从以上问题的解决中,你知道解决这些问题的关键是什么吗?
关键是:把一个数式化成了几个数的积的形式,即因数分解。
99 –99还能被哪些正整数整除?
3
993-99=99x992-99x1
=99(992-1)
=99(99+1)(99-1)
=98x99x100
所以,993-99能被100整除。
(尽量独立思考,有困难的同学参考教材92页议一议上边的部分)
将99换成其他任意一个大于1的整数,上述结论仍然成立吗?
用a表示任意一个大于1的整数,则你能把
上面式子化成了几个整式积的形式
化成几个整式的乘积的形式吗?
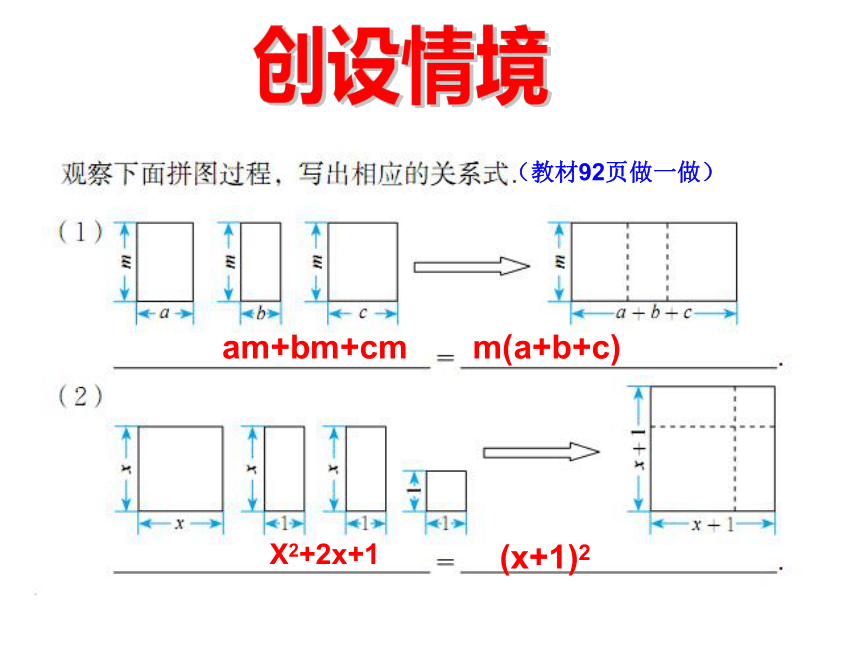
am+bm+cm
m(a+b+c)
X2+2x+1
(x+1)2
(教材92页做一做)
1、阅读教材93页“做一做”上边的内容,了解因式分解的意义。
2、完成教材93页“做一做” 的内容,初步体会因式分解与整式乘法的联系。
3、结合教材93页“做一做” 的内容,想一想因式分解与整式乘法有什么联系?并举例说明。
先独立完成,然后再小组交流
1、把一个多项式化成____________的形式,这种变形叫做因式分解。因式分解也可称为________。
几个整式的积
分解因式
2、计算下列式子:
(1)3x(x-1)= ; (2)m(a+b-1)= ;
(3)(m+4)(m-4)= ;(4)(y-3) = ;
2
3x -3x
2
ma+mb-m
m -16
2
y -6y+9
2
根据上面的算式填空:
(1)ma+mb-m = ;(2)3x -3x= ;
(3)m -16= ;(4)y -6y+9= .
2
2
2
m(a+b-1)
3x(x-1)
(m+4)(m-4)
(y-3)
3、分解因式与整式乘法是互逆关系
(1)把几个整式的积化成一个多项式的形式,是________.
(2)把一个多项式化成几个整式的积的形式,是________.
整式乘法
因式分解
2
把左右两边对应的式子连起来,并说明哪些变形是因式分解,哪些是整式乘法.
整式乘法
因式分解
整式乘法
因式分解
下面是数学课上老师与学生的一段对话,阅读后请填空:
老师:式子x2+4-4x=x(x-4)+4 从左到右的变形是因式分解吗?
学生:我认为不是。
老师:为什么?
学生:因为因式分解的结果必须是_______的形式
老师:回答的很好!请同学们继续观察:式子x2+x=x2(1+ ),从左到右的变形是因式分解吗?
学生;不是。
老师:这个式子从左到右的变形也是和差化积的形式,为什么不是分解因式哪?
学生:因为每个因式必须是_________.
老师:正确!
积
整式
选择题.
1、下列从左到右的变形为分解因式的是( ).
A.12a2b=3a·4ab
B.(x+2)(x-2)=x2-4
C.4x2-8x-1=4x(x-2)-1
D.12ax-12ay=12a(x-y).
2、(3a-y)(3a+y)是下列哪一个多项式分解因式的结果( ).
A.9a2+y2 B.-9a2+y2
C.9a2-y2 D.-9a2-y2
D
C
1、若 —x—m=(x+2)(x-3)
则m=_______
2、若 +ax+b 能分解成(x-1)(x-4),
则a=___,b=___
6
-5
4
1、若 —x—m=(x+2)(x-3)
则m=_______
6
解:∵x2-x-m=(x+2)(x-3)
∴ x2-x-m=x2-x-6
∴m=6
2、若 +ax+b 能分解成(x-1)(x-4),
则a=___,b=___
-5
4
解:∵x2+ax+b 能分解成(x-1)(x-4)
∴x2+ax+b=(x-1)(x-4)
∴x2+ax+b=x2-5x+4
∴a=-5, b=4
的值
求
时,
1当
ac
ab
c
b
a
-
=
=
=
386
.
1
,
386
.
2
,
14
.
3
2、已知多项式x2+2x+p因式分解后有一个因式为x-3,求p的值
解:∵ab-ac=a(b-c)
∴当a=3.14,b=2.386,c=1.386时
原式=3.14X(2.386-1.386)
=3.14X1
=3.14
1.当a=3.14,b=2.386,c=1.386时, 求ab-ac的值
2、已知多项式x2+2x+p因式分解后有一个因式为x-3,求p的值
解:∵多项式x2+2x+p因式分解后有一个因式为x-3
∴当x-3=0,即x=3时
x2+2x+p=0,即32+2x3+P=0
∴P=-15
解:设另一个因式为x+a,则有
x2+2x+p=(x-3)(x+a)
∴ x2+2x+p=x2+(a-3)x-3a
∴a-3=2, p=-3a
∴a=5, p=-15
意义
与整式乘法关系
应用
整式的乘法运算是积化和差;
多项式因式分解是和差化积
因式分解是把一个多项式化为几个整式乘积的形式,特征是和差化积
因式分解与整式乘法是方向相反的两种恒等变形,即互逆关系
1.分解的对象必须是多项式.
2.分解的结果一定是几个整式的乘积的形式.
作 业
教材94页习题4.1
一、用简便方法计算:(先说结果后说方法)
(1) =
(2)-2.67× 132+25×2.67+7×2.67=
(3)99 –1= .
7
9
× 13 – × 6+ × 2
7
9
7
9
2
7
-267
9800
=(13-6+2)X =9X
7
9
=2.67x(-132+25+7)=2.67X(-100)
=(99+1)(99-1)=100x98
7
9
二、99 –99能被100整除吗?你是怎样想的?
3
从以上问题的解决中,你知道解决这些问题的关键是什么吗?
关键是:把一个数式化成了几个数的积的形式,即因数分解。
99 –99还能被哪些正整数整除?
3
993-99=99x992-99x1
=99(992-1)
=99(99+1)(99-1)
=98x99x100
所以,993-99能被100整除。
(尽量独立思考,有困难的同学参考教材92页议一议上边的部分)
将99换成其他任意一个大于1的整数,上述结论仍然成立吗?
用a表示任意一个大于1的整数,则你能把
上面式子化成了几个整式积的形式
化成几个整式的乘积的形式吗?
am+bm+cm
m(a+b+c)
X2+2x+1
(x+1)2
(教材92页做一做)
1、阅读教材93页“做一做”上边的内容,了解因式分解的意义。
2、完成教材93页“做一做” 的内容,初步体会因式分解与整式乘法的联系。
3、结合教材93页“做一做” 的内容,想一想因式分解与整式乘法有什么联系?并举例说明。
先独立完成,然后再小组交流
1、把一个多项式化成____________的形式,这种变形叫做因式分解。因式分解也可称为________。
几个整式的积
分解因式
2、计算下列式子:
(1)3x(x-1)= ; (2)m(a+b-1)= ;
(3)(m+4)(m-4)= ;(4)(y-3) = ;
2
3x -3x
2
ma+mb-m
m -16
2
y -6y+9
2
根据上面的算式填空:
(1)ma+mb-m = ;(2)3x -3x= ;
(3)m -16= ;(4)y -6y+9= .
2
2
2
m(a+b-1)
3x(x-1)
(m+4)(m-4)
(y-3)
3、分解因式与整式乘法是互逆关系
(1)把几个整式的积化成一个多项式的形式,是________.
(2)把一个多项式化成几个整式的积的形式,是________.
整式乘法
因式分解
2
把左右两边对应的式子连起来,并说明哪些变形是因式分解,哪些是整式乘法.
整式乘法
因式分解
整式乘法
因式分解
下面是数学课上老师与学生的一段对话,阅读后请填空:
老师:式子x2+4-4x=x(x-4)+4 从左到右的变形是因式分解吗?
学生:我认为不是。
老师:为什么?
学生:因为因式分解的结果必须是_______的形式
老师:回答的很好!请同学们继续观察:式子x2+x=x2(1+ ),从左到右的变形是因式分解吗?
学生;不是。
老师:这个式子从左到右的变形也是和差化积的形式,为什么不是分解因式哪?
学生:因为每个因式必须是_________.
老师:正确!
积
整式
选择题.
1、下列从左到右的变形为分解因式的是( ).
A.12a2b=3a·4ab
B.(x+2)(x-2)=x2-4
C.4x2-8x-1=4x(x-2)-1
D.12ax-12ay=12a(x-y).
2、(3a-y)(3a+y)是下列哪一个多项式分解因式的结果( ).
A.9a2+y2 B.-9a2+y2
C.9a2-y2 D.-9a2-y2
D
C
1、若 —x—m=(x+2)(x-3)
则m=_______
2、若 +ax+b 能分解成(x-1)(x-4),
则a=___,b=___
6
-5
4
1、若 —x—m=(x+2)(x-3)
则m=_______
6
解:∵x2-x-m=(x+2)(x-3)
∴ x2-x-m=x2-x-6
∴m=6
2、若 +ax+b 能分解成(x-1)(x-4),
则a=___,b=___
-5
4
解:∵x2+ax+b 能分解成(x-1)(x-4)
∴x2+ax+b=(x-1)(x-4)
∴x2+ax+b=x2-5x+4
∴a=-5, b=4
的值
求
时,
1当
ac
ab
c
b
a
-
=
=
=
386
.
1
,
386
.
2
,
14
.
3
2、已知多项式x2+2x+p因式分解后有一个因式为x-3,求p的值
解:∵ab-ac=a(b-c)
∴当a=3.14,b=2.386,c=1.386时
原式=3.14X(2.386-1.386)
=3.14X1
=3.14
1.当a=3.14,b=2.386,c=1.386时, 求ab-ac的值
2、已知多项式x2+2x+p因式分解后有一个因式为x-3,求p的值
解:∵多项式x2+2x+p因式分解后有一个因式为x-3
∴当x-3=0,即x=3时
x2+2x+p=0,即32+2x3+P=0
∴P=-15
解:设另一个因式为x+a,则有
x2+2x+p=(x-3)(x+a)
∴ x2+2x+p=x2+(a-3)x-3a
∴a-3=2, p=-3a
∴a=5, p=-15
意义
与整式乘法关系
应用
整式的乘法运算是积化和差;
多项式因式分解是和差化积
因式分解是把一个多项式化为几个整式乘积的形式,特征是和差化积
因式分解与整式乘法是方向相反的两种恒等变形,即互逆关系
1.分解的对象必须是多项式.
2.分解的结果一定是几个整式的乘积的形式.
作 业
教材94页习题4.1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
