人教版三年级数学上册 8—1分数的初步认识 一课一练 精讲精练+奥数培优(无答案)
文档属性
| 名称 | 人教版三年级数学上册 8—1分数的初步认识 一课一练 精讲精练+奥数培优(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 00:00:00 | ||
图片预览


文档简介
分数的初步认识
知识引入:
一、几分之一和几分之几
例题1:读一读、写一写。
例题2:我是小法官。(对的画“√”,错的画“×”)
例题3:看图填空。
例题4:在○里填上“>” “<”或“=”。
知识精讲1:
1. 把一个物体或图形平均分成几份,取其中的1份就是它的几分之一,2份就是它的几分之二,3份就是它的几分之三……
2. 把一个物体或图形平均分成几份,分母就是几,表示这样的几份,分子就是几。
3.同分母分数的大小比较:
(1)同分母分数,分子大的分数大,分子小的分数小;
(2)一个分数的分子和分母相同时,表示把一个物体或图形平均分成几份,取的份数与分的份数一样多,也就是1。
4.同分子分数的大小比较:同分子分数,分母大的分数小,分母小的分数大。
二、分数的简单计算
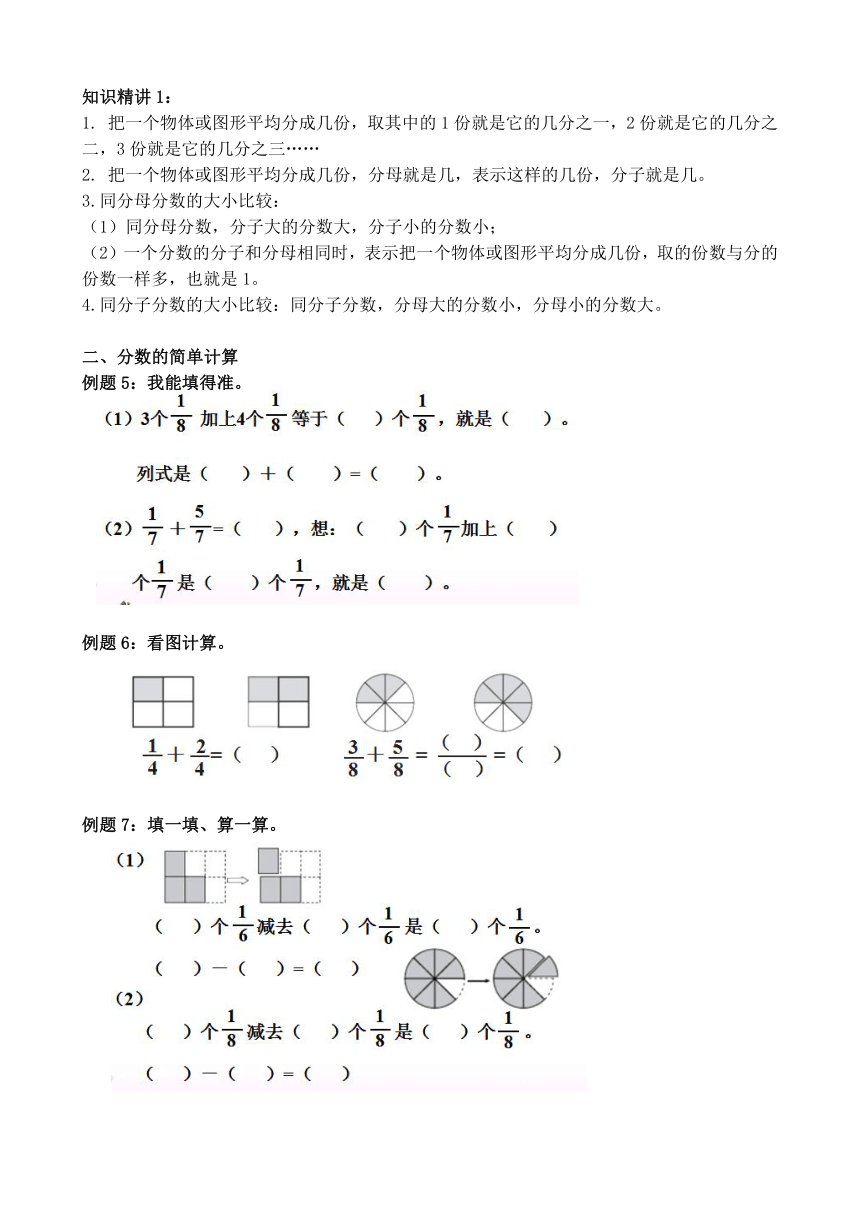
例题5:我能填得准。
例题6:看图计算。
例题7:填一填、算一算。
例题8:比一比。(在 里填上“>”“<”或“=”)
知识精讲2:
1.同分母分数的加、减法:分母不变,分子相加、减。
2.1减去几分之几: 1可以看作是分子和分母相同的分数,然后分母不变,分子相减。
三、分数的简单应用(一)
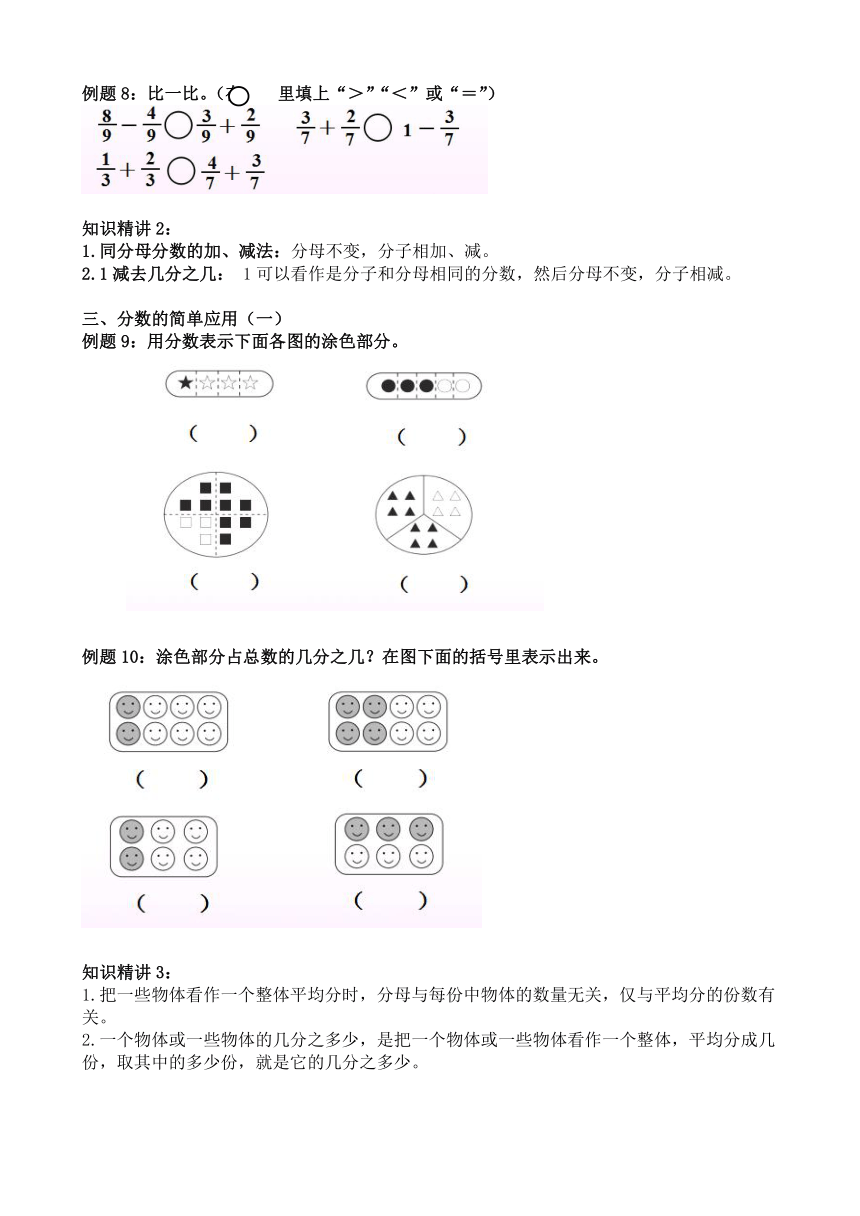
例题9:用分数表示下面各图的涂色部分。
例题10:涂色部分占总数的几分之几?在图下面的括号里表示出来。
知识精讲3:
1.把一些物体看作一个整体平均分时,分母与每份中物体的数量无关,仅与平均分的份数有关。
2.一个物体或一些物体的几分之多少,是把一个物体或一些物体看作一个整体,平均分成几份,取其中的多少份,就是它的几分之多少。
四、分数的简单应用(二)
例题11:我是口算小能手。
例题12:分一分,算一算。
例题13:填一填。
知识精讲4:求一个数的几分之几
求一个数的几分之几是多少,就是用这个数除以分母(求出一份的数是多少),再用商(每份数)乘分子。
巩固练习:
1.计算。
+ = -= +=
+ = -= -=
+= +=
2.填一填。
(1)+=( ),( )个加( )个是( )个,就是( )。
(2)-=( ),( )个减( )个,剩( )个,就是( ) 。(3)比多( )个
(4)妈妈买了9支铅笔,给小冬5支,小立4支,小冬拿了这些铅笔的( ),小立拿了这些铅笔的( )。
3.判断。(对的打“√”错的打“×”)
(1)1个 加上2个 是3个 ,就是 。( )
(2)+=( )
(3)一根绳子用去,还剩下这根绳子的。( )
(4)把一块蛋糕分成了4份,其中的一份是这块蛋糕的。( )
4.看图写算式。
5. 填一填。
1份是,有( )个。 2份是,有( )个。
2份是,有( )个。 3份是,有( )个。
6.先分一分,再根据下面的分数涂上喜欢的颜色。
7. 用分数填空。
8. 24名同学进行队列表演,每4人一行,可以排( )行,每行占总人数的,3行占总人数的,是( )人。.如果每8人一行,可以排( )行,每行占总人数的,2行占总人数的,是( )人。
三年级同学参加舞蹈小组的人数是参加体育小组人数的,参加体育小组的有20人。参加
舞蹈小组的有多少人?
奥数思维拓展:计量单位与分数
渗透两种数学思想:数形结合思想、推理思想。
学习两类思维方法:观察法、迁移法。
[例题]在( )里填上合适的分数。
1厘米=( )分米 1克=( )千克
[分析]
[技巧]
两个计量单位之间的进率是几,低级单位就可以看作把高级单位平均分成几份,取其中的一份,即低级单位占高级单位的几分之几。
[举一反三]
先写出合适的分数,在任选两个说说你是怎么想的。
知识引入:
一、几分之一和几分之几
例题1:读一读、写一写。
例题2:我是小法官。(对的画“√”,错的画“×”)
例题3:看图填空。
例题4:在○里填上“>” “<”或“=”。
知识精讲1:
1. 把一个物体或图形平均分成几份,取其中的1份就是它的几分之一,2份就是它的几分之二,3份就是它的几分之三……
2. 把一个物体或图形平均分成几份,分母就是几,表示这样的几份,分子就是几。
3.同分母分数的大小比较:
(1)同分母分数,分子大的分数大,分子小的分数小;
(2)一个分数的分子和分母相同时,表示把一个物体或图形平均分成几份,取的份数与分的份数一样多,也就是1。
4.同分子分数的大小比较:同分子分数,分母大的分数小,分母小的分数大。
二、分数的简单计算
例题5:我能填得准。
例题6:看图计算。
例题7:填一填、算一算。
例题8:比一比。(在 里填上“>”“<”或“=”)
知识精讲2:
1.同分母分数的加、减法:分母不变,分子相加、减。
2.1减去几分之几: 1可以看作是分子和分母相同的分数,然后分母不变,分子相减。
三、分数的简单应用(一)
例题9:用分数表示下面各图的涂色部分。
例题10:涂色部分占总数的几分之几?在图下面的括号里表示出来。
知识精讲3:
1.把一些物体看作一个整体平均分时,分母与每份中物体的数量无关,仅与平均分的份数有关。
2.一个物体或一些物体的几分之多少,是把一个物体或一些物体看作一个整体,平均分成几份,取其中的多少份,就是它的几分之多少。
四、分数的简单应用(二)
例题11:我是口算小能手。
例题12:分一分,算一算。
例题13:填一填。
知识精讲4:求一个数的几分之几
求一个数的几分之几是多少,就是用这个数除以分母(求出一份的数是多少),再用商(每份数)乘分子。
巩固练习:
1.计算。
+ = -= +=
+ = -= -=
+= +=
2.填一填。
(1)+=( ),( )个加( )个是( )个,就是( )。
(2)-=( ),( )个减( )个,剩( )个,就是( ) 。(3)比多( )个
(4)妈妈买了9支铅笔,给小冬5支,小立4支,小冬拿了这些铅笔的( ),小立拿了这些铅笔的( )。
3.判断。(对的打“√”错的打“×”)
(1)1个 加上2个 是3个 ,就是 。( )
(2)+=( )
(3)一根绳子用去,还剩下这根绳子的。( )
(4)把一块蛋糕分成了4份,其中的一份是这块蛋糕的。( )
4.看图写算式。
5. 填一填。
1份是,有( )个。 2份是,有( )个。
2份是,有( )个。 3份是,有( )个。
6.先分一分,再根据下面的分数涂上喜欢的颜色。
7. 用分数填空。
8. 24名同学进行队列表演,每4人一行,可以排( )行,每行占总人数的,3行占总人数的,是( )人。.如果每8人一行,可以排( )行,每行占总人数的,2行占总人数的,是( )人。
三年级同学参加舞蹈小组的人数是参加体育小组人数的,参加体育小组的有20人。参加
舞蹈小组的有多少人?
奥数思维拓展:计量单位与分数
渗透两种数学思想:数形结合思想、推理思想。
学习两类思维方法:观察法、迁移法。
[例题]在( )里填上合适的分数。
1厘米=( )分米 1克=( )千克
[分析]
[技巧]
两个计量单位之间的进率是几,低级单位就可以看作把高级单位平均分成几份,取其中的一份,即低级单位占高级单位的几分之几。
[举一反三]
先写出合适的分数,在任选两个说说你是怎么想的。
