人教版六年级数学下册总复习图形与几何-图形的认识与测量课件(共53张PPT)
文档属性
| 名称 | 人教版六年级数学下册总复习图形与几何-图形的认识与测量课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 866.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-17 22:33:38 | ||
图片预览






文档简介
(共53张PPT)
总复习
人教版六年级数学下册第六单元
图形的认识与测量
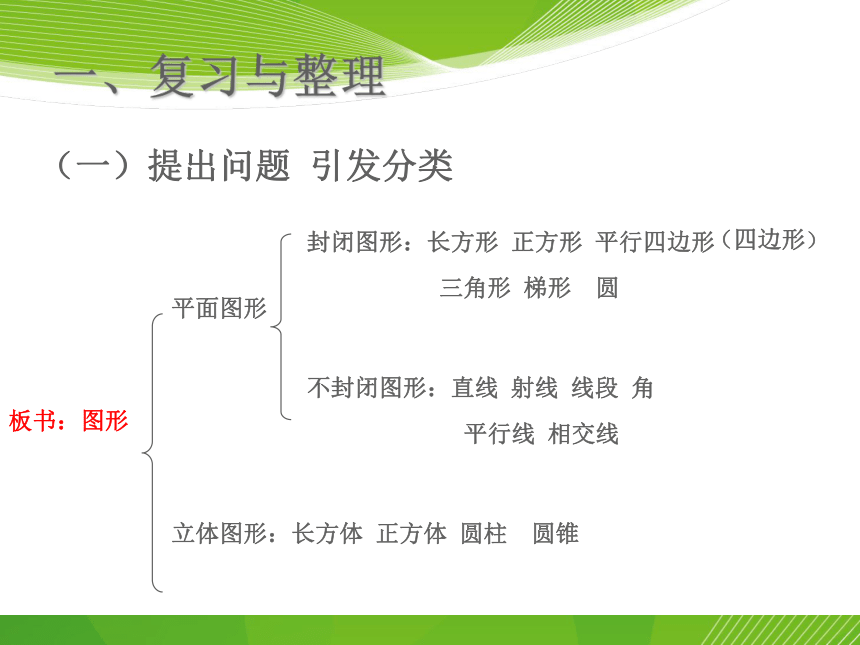
一、复习与整理
(一)提出问题 引发分类
(四边形)
A
直线
A
射线
A
B
线段
A
B
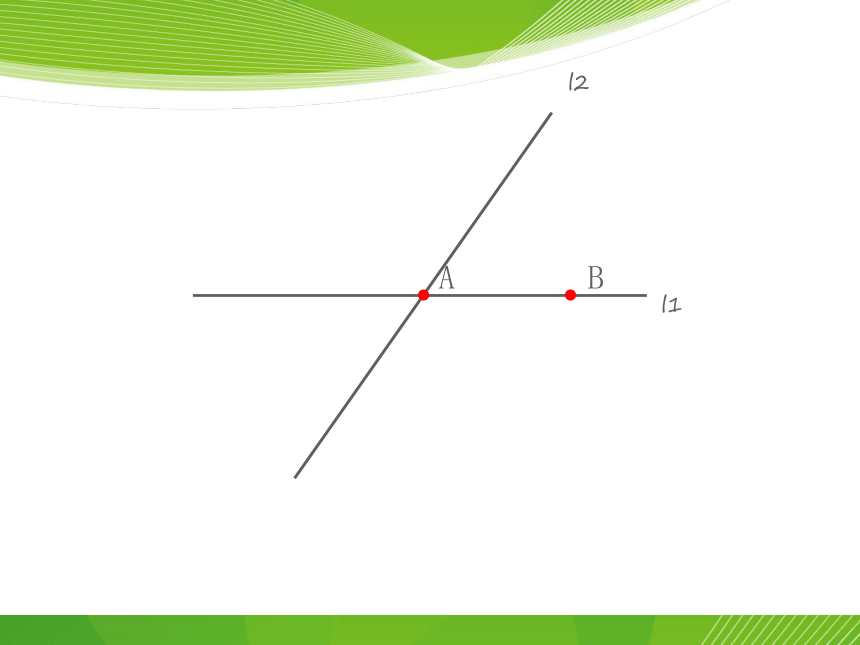
l2
l1
A
B
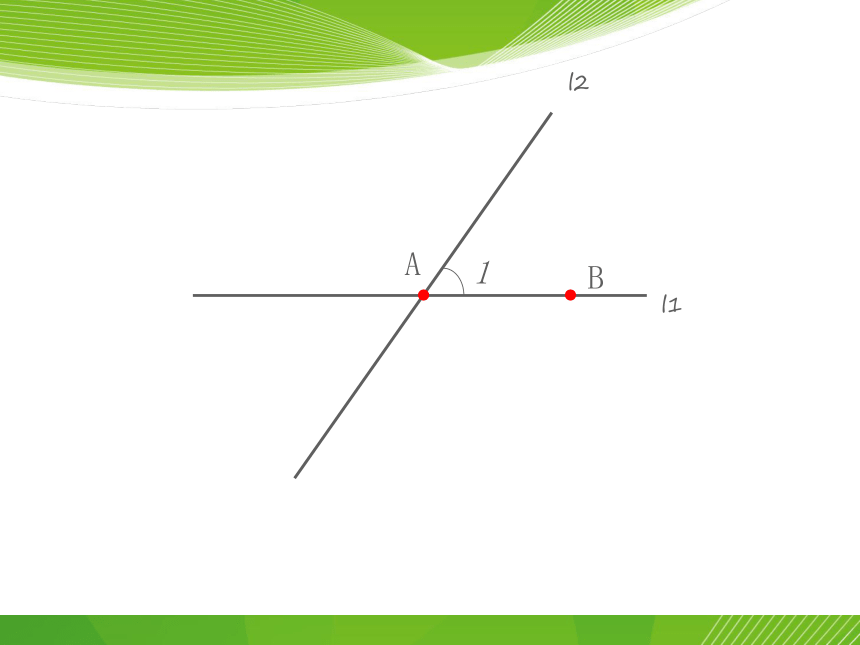
1
l1
l2
A
B
1
l1
l2
顶点
边
边
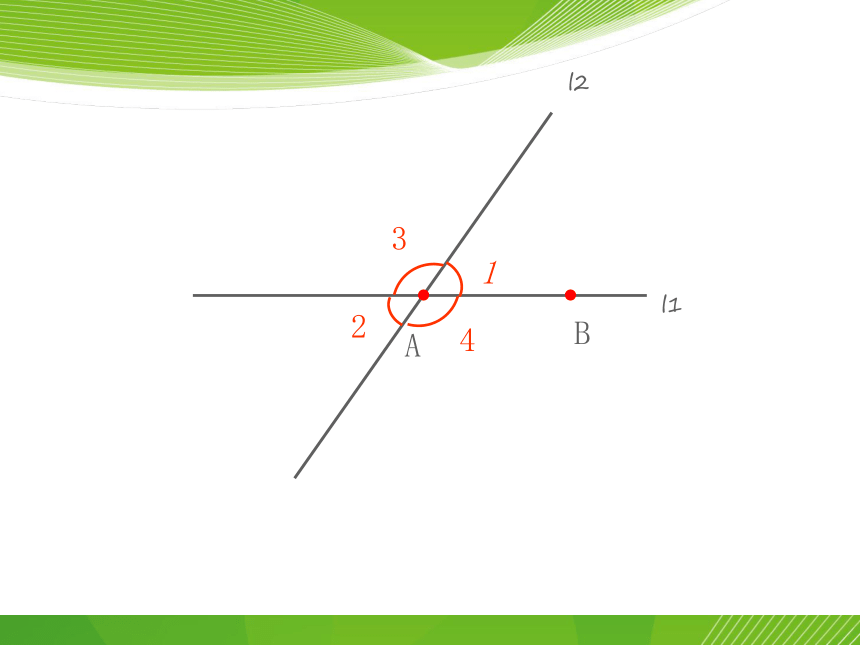
A
B
1
l1
l2
2
4
3
l1
l2
A
B
1
3
l1
l2
A
B
平角
l1
l2
A
B
周角
B
A
l2
l1
l1
l2
A
B
1
l1
l2
A
B
l3
一、判断对错
1、同一平面内,平行的 两条直线永不相交。( )
2、平角就是一条直线。( )
3、两点确定一条线段。( )
4、过一点只能做一条直线。( )
√
×
√
×
线外一点到直线的所有线段中,
垂线最短。
平面图形的周长:
围成平面图形的所有边长的总和,叫做平面图形的周长。
平面图形的面积:
物体表面的大小或物体所占平面的大小,叫做面积。
三角形:
(一)三角形的概念
由三条线段围成的封闭图形叫做三角形。
三角形具有稳定性(不易变形);三角形的三个内角和是180°。
底
高
(底)
(高)
底
高
底
高
底
高
(二)三角形的分类
三角形按角分
锐角三角形
直角三角形
钝角三角形
(三个角都是锐角)
(有一个角是直角)
(有一个角是钝角)
一个三角形里最多会有几个钝角?最多会有几个直角?最多会有几个锐角?最少会有几个锐角?
一个三角形里最多会有一个钝角,最多会有一个直角,最多会有三个锐角,最少会有两个锐角。
三角形
等腰三角形
等边三角形
(二)三角形的分类
三角形按边分
(两条边相等)
(三条边都相等)
不规则三角形
(三条边都不相等)
等腰三角形
腰
腰
底
顶角
底角
底角
腰
顶角
腰
底角
底角
底
等腰直角三角形
腰
腰
底
顶角
底角
底角
等腰三角形
等腰三角形
有两条边相等的三角形叫做等腰三角形,其中相等的两条边叫做腰,另一条叫做底。两条腰的夹角叫做顶角,腰和底边夹角叫做底角,等腰三角形的两个底的角度数相等。
边
边
边
等边三角形
三条边都相等的三角形叫做等边三角形,又叫正三角形。等边三角形的三条边长度相等,三个角的大小相等,都是60°。
等边三角形是特殊的等腰三角形。
13cm
5cm
7cm
三角形其中两条线段的和大于第三条线段时,这样的三条线段才能组成一个三角形。
线外一点到直线的所有线段中,
垂线最短。
在能围成三角形的一组线段下面的括号里画“ ”
0.5cm
1.8cm
1cm
1cm
2.5cm
3cm
4cm
2cm
2cm
( )
( )
( )
一、填一填
2.直角三角形的一个锐角是56 o,∠1是( ) o。
34
560
1
四边形:
(一)四边形的概念
由四条线段围成的封闭图形叫做四边形。
四边形具有不稳定性(容易变形);四边形的四个内角和是360°。
梯 形
只有一组对边平行的四边形叫做梯形。
在梯形里,互相平行的一组对边叫做梯形的上底和下底,不平行的一组叫做梯形的腰,上底和下底之间的距离叫做梯形的高。
两腰相等的梯形叫做等腰梯形;有一个直角的梯形叫做直角梯形。
上底
下底
腰
腰
高
普通梯形
等腰梯形
直角梯形
平行四边形
两组对边分别平行的四边形叫做平行四边形。平行四边形对边的长度相等,对角的大小也相等。
从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,这条边叫做平行四边形的底。
四条边相等的平行四边形叫做菱形。
底
高
平行四边形
高
底
菱形
长方形
两组对边分别平行并且相等,四个角都是直角的四边形叫做长方形。
长方形中较长的一组对边叫做长方形的长,较短的一组对边叫做长方形的宽。
长方形是特殊的平行四边形。
长
宽
长方形
长方形
长
宽
正方形
四条边相等,四个角都是直角的四边形叫做正方形。
正方形是特殊的长方形。
正方形
(二)四边形的分类
四边形
两组对边互不平行
只有一组对边平行
不规则四边形
梯形
两组对边分别平行
平行四边形
四个角
都是直角
长方形
四条边
都相等
正方形
四条边
都相等
菱形
四个角
都是直角
两腰相等
等腰梯形
有一个角是直角
直角梯形
也可以用下图表示:
四边形
不规则四边形
梯形
平行四边形
长方形
正方形
菱形
等腰梯形
直角梯形
圆形:
(一)圆形的概念
在一个平面上,到定点距离相等的点的轨迹叫做圆。
画圆时,固定的一点叫做圆心(o),从圆心到圆上任意一点的线段叫做半径(r),半径有无数条;通过圆心并且两端都在圆上的线段叫做直径(d),直径有无数条。圆心决定圆的位置,半径(直径)决定圆的大小。
同圆或等圆中,所有的直径都相等,所有的半径也相等,直径的长度是半径的两倍(半径的长度是直径的二分之一)。
·
O
圆心
半径r
直径d
·
(二)圆环的概念
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
(三)扇形的概念
扇形是圆的一部分,扇形的大小与圆心角的度数有关系。
a
b
a
a
a
h
a
h
a
b
h
r
平面图形的周长和面积公式推导:
平行四边形:
长方形:
三角形:
梯形:
与平面图形周长、面积有关的计算公式:
正方形:
r=d÷2
r=C÷π÷2
d=2r
d=C÷π
C=2πr
C=πd
S=πr2
S=π(d÷2)2
S=π(C÷π÷2)2
与圆有关的计算公式
圆环面积:
S环=πR2 -πr2
S环=π(R2 -r2)
扇形面积:
知道半径
(r) 知道直径
(d) 知道周长
(C)
求半径(r)
求直径(d)
求周长(C)
求面积(S)
A B C D E F G
H I J K L M N
O P Q R S T U
V W X Y Z
下面哪些字母是轴对称字母?
A
B
H
I
M
O
T
U
V
W
X
Y
K
E
D
C
二、回顾梳理 构建联系
(三)复习立体图形的特征、联系及公式
立体图形 棱长总和 表面积 体积(容积)
长方体
正方体
圆柱 -
圆锥 - -
三、图形公式
(三)复习立体图形的特征、联系及公式
提问9:这些图形有没有一个共同的体积计算公式呢?
课件出示:
基本练习:
将一个棱长为4分米的正方体钢材熔铸成底面半径为4分米的圆柱体,这个圆柱有多长?
二、巩固练习
1. 求涂色部分的面积。(单位:cm)
提问1:要求涂色部分的面积,你会做吗?请你先试着做一做,看看你
都能想到哪些不同的方法?
预设1:梯形面积―三角形面积 (4+12)×4÷2-4×4÷2
预设2:大梯形面积 (4+8)×4÷2
预设3:小三角形面积+大三角形面积 4×4÷2+8×4÷2
提问2:你能读懂他们的想法吗?指名解读同伴的想法。
1、面积相等的两个梯形一定可以拼成一个平行四
边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一
定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方
厘米。( )
判 断
×
×
√
×
×
例题:
工地上有一些沙子,堆起来近似于一个圆锥,这堆沙子大约多少立方米?(得数保留两位小数)
3.14×4
12.56(平方米)
5.024≈5.02(立方米)
回顾一下,今天这节课你有哪些收获和体会?
总复习
人教版六年级数学下册第六单元
图形的认识与测量
一、复习与整理
(一)提出问题 引发分类
(四边形)
A
直线
A
射线
A
B
线段
A
B
l2
l1
A
B
1
l1
l2
A
B
1
l1
l2
顶点
边
边
A
B
1
l1
l2
2
4
3
l1
l2
A
B
1
3
l1
l2
A
B
平角
l1
l2
A
B
周角
B
A
l2
l1
l1
l2
A
B
1
l1
l2
A
B
l3
一、判断对错
1、同一平面内,平行的 两条直线永不相交。( )
2、平角就是一条直线。( )
3、两点确定一条线段。( )
4、过一点只能做一条直线。( )
√
×
√
×
线外一点到直线的所有线段中,
垂线最短。
平面图形的周长:
围成平面图形的所有边长的总和,叫做平面图形的周长。
平面图形的面积:
物体表面的大小或物体所占平面的大小,叫做面积。
三角形:
(一)三角形的概念
由三条线段围成的封闭图形叫做三角形。
三角形具有稳定性(不易变形);三角形的三个内角和是180°。
底
高
(底)
(高)
底
高
底
高
底
高
(二)三角形的分类
三角形按角分
锐角三角形
直角三角形
钝角三角形
(三个角都是锐角)
(有一个角是直角)
(有一个角是钝角)
一个三角形里最多会有几个钝角?最多会有几个直角?最多会有几个锐角?最少会有几个锐角?
一个三角形里最多会有一个钝角,最多会有一个直角,最多会有三个锐角,最少会有两个锐角。
三角形
等腰三角形
等边三角形
(二)三角形的分类
三角形按边分
(两条边相等)
(三条边都相等)
不规则三角形
(三条边都不相等)
等腰三角形
腰
腰
底
顶角
底角
底角
腰
顶角
腰
底角
底角
底
等腰直角三角形
腰
腰
底
顶角
底角
底角
等腰三角形
等腰三角形
有两条边相等的三角形叫做等腰三角形,其中相等的两条边叫做腰,另一条叫做底。两条腰的夹角叫做顶角,腰和底边夹角叫做底角,等腰三角形的两个底的角度数相等。
边
边
边
等边三角形
三条边都相等的三角形叫做等边三角形,又叫正三角形。等边三角形的三条边长度相等,三个角的大小相等,都是60°。
等边三角形是特殊的等腰三角形。
13cm
5cm
7cm
三角形其中两条线段的和大于第三条线段时,这样的三条线段才能组成一个三角形。
线外一点到直线的所有线段中,
垂线最短。
在能围成三角形的一组线段下面的括号里画“ ”
0.5cm
1.8cm
1cm
1cm
2.5cm
3cm
4cm
2cm
2cm
( )
( )
( )
一、填一填
2.直角三角形的一个锐角是56 o,∠1是( ) o。
34
560
1
四边形:
(一)四边形的概念
由四条线段围成的封闭图形叫做四边形。
四边形具有不稳定性(容易变形);四边形的四个内角和是360°。
梯 形
只有一组对边平行的四边形叫做梯形。
在梯形里,互相平行的一组对边叫做梯形的上底和下底,不平行的一组叫做梯形的腰,上底和下底之间的距离叫做梯形的高。
两腰相等的梯形叫做等腰梯形;有一个直角的梯形叫做直角梯形。
上底
下底
腰
腰
高
普通梯形
等腰梯形
直角梯形
平行四边形
两组对边分别平行的四边形叫做平行四边形。平行四边形对边的长度相等,对角的大小也相等。
从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,这条边叫做平行四边形的底。
四条边相等的平行四边形叫做菱形。
底
高
平行四边形
高
底
菱形
长方形
两组对边分别平行并且相等,四个角都是直角的四边形叫做长方形。
长方形中较长的一组对边叫做长方形的长,较短的一组对边叫做长方形的宽。
长方形是特殊的平行四边形。
长
宽
长方形
长方形
长
宽
正方形
四条边相等,四个角都是直角的四边形叫做正方形。
正方形是特殊的长方形。
正方形
(二)四边形的分类
四边形
两组对边互不平行
只有一组对边平行
不规则四边形
梯形
两组对边分别平行
平行四边形
四个角
都是直角
长方形
四条边
都相等
正方形
四条边
都相等
菱形
四个角
都是直角
两腰相等
等腰梯形
有一个角是直角
直角梯形
也可以用下图表示:
四边形
不规则四边形
梯形
平行四边形
长方形
正方形
菱形
等腰梯形
直角梯形
圆形:
(一)圆形的概念
在一个平面上,到定点距离相等的点的轨迹叫做圆。
画圆时,固定的一点叫做圆心(o),从圆心到圆上任意一点的线段叫做半径(r),半径有无数条;通过圆心并且两端都在圆上的线段叫做直径(d),直径有无数条。圆心决定圆的位置,半径(直径)决定圆的大小。
同圆或等圆中,所有的直径都相等,所有的半径也相等,直径的长度是半径的两倍(半径的长度是直径的二分之一)。
·
O
圆心
半径r
直径d
·
(二)圆环的概念
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
(三)扇形的概念
扇形是圆的一部分,扇形的大小与圆心角的度数有关系。
a
b
a
a
a
h
a
h
a
b
h
r
平面图形的周长和面积公式推导:
平行四边形:
长方形:
三角形:
梯形:
与平面图形周长、面积有关的计算公式:
正方形:
r=d÷2
r=C÷π÷2
d=2r
d=C÷π
C=2πr
C=πd
S=πr2
S=π(d÷2)2
S=π(C÷π÷2)2
与圆有关的计算公式
圆环面积:
S环=πR2 -πr2
S环=π(R2 -r2)
扇形面积:
知道半径
(r) 知道直径
(d) 知道周长
(C)
求半径(r)
求直径(d)
求周长(C)
求面积(S)
A B C D E F G
H I J K L M N
O P Q R S T U
V W X Y Z
下面哪些字母是轴对称字母?
A
B
H
I
M
O
T
U
V
W
X
Y
K
E
D
C
二、回顾梳理 构建联系
(三)复习立体图形的特征、联系及公式
立体图形 棱长总和 表面积 体积(容积)
长方体
正方体
圆柱 -
圆锥 - -
三、图形公式
(三)复习立体图形的特征、联系及公式
提问9:这些图形有没有一个共同的体积计算公式呢?
课件出示:
基本练习:
将一个棱长为4分米的正方体钢材熔铸成底面半径为4分米的圆柱体,这个圆柱有多长?
二、巩固练习
1. 求涂色部分的面积。(单位:cm)
提问1:要求涂色部分的面积,你会做吗?请你先试着做一做,看看你
都能想到哪些不同的方法?
预设1:梯形面积―三角形面积 (4+12)×4÷2-4×4÷2
预设2:大梯形面积 (4+8)×4÷2
预设3:小三角形面积+大三角形面积 4×4÷2+8×4÷2
提问2:你能读懂他们的想法吗?指名解读同伴的想法。
1、面积相等的两个梯形一定可以拼成一个平行四
边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一
定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方
厘米。( )
判 断
×
×
√
×
×
例题:
工地上有一些沙子,堆起来近似于一个圆锥,这堆沙子大约多少立方米?(得数保留两位小数)
3.14×4
12.56(平方米)
5.024≈5.02(立方米)
回顾一下,今天这节课你有哪些收获和体会?
