人教版数学八年级下册19.2.3一次函数与方程、不等式课件 (共39张PPT)
文档属性
| 名称 | 人教版数学八年级下册19.2.3一次函数与方程、不等式课件 (共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 870.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 21:32:33 | ||
图片预览










文档简介
(共39张PPT)
八年级 下册
19.2.3 一次函数与方程、不等式
本课是在学习一次函数的基础上,讨论一次函数与
二元一次方程的关系,用函数的观点看一元一次方
程、一元一次不等式、二元一次方程组.从而建立
它们之间的联系.
课件说明
课件说明
学习目标:
1.认识一次函数与一元(二元)一次方程(组)、
一元一次不等式之间的联系.会用函数观点解释
方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进
一步体会“以形表示数,以数解释形”的数形结
合思想.
学习重点:
理解一次函数与二元一次方程(组)的联系.
问题①:解方程2x+20=0
问题②:当x为何值时,函数y=2x+20的值0?
问题③:画出函数y=2x+20的图象,并确定
它与x轴的交点坐标;
问题④:问题① ②有何关系? ① ③呢?
x=-10
当x=-10时,函数y=2x+20的值0.
问题①:解方程2x+20=0
问题②:当x为何值时,函数y=2x+20的值0?
问题③:画出函数y=2x+20
的图象,并确定
它与x轴的交点坐标;
问题④:问题① ②有何关系? ① ③呢?
问题①与问题②可以看作是同一个问题两种形式.
问题① ②是从数的角度看,问题③是从图形的角度看.
直线y=2x+20与x轴的交点坐标为(-10,0)
1、方程ax+b=0(a、b为常数a≠0)的解是 .
2、当x 时,一次函数y= ax+b( a≠0)的值0?
3、直线y= ax+b 与x轴的交点坐标是 .
归纳
任何一个一元一次方程都可化为ax+b=0(a、b为常数,a≠0)的形式,所以解一元一次方程ax+b=0可转化为“当一次函数y=ax+b值为0时,求相应的自变量x的值.”
从图象上看,这又相当于“求直线y= ax+b 与x轴的交点的横坐标的值”
解方程
ax+b=0
求当x为何值时,
一次函数y=ax +b的值为0?
求函数y=ax +b
的图象与x轴交点
的横坐标的值
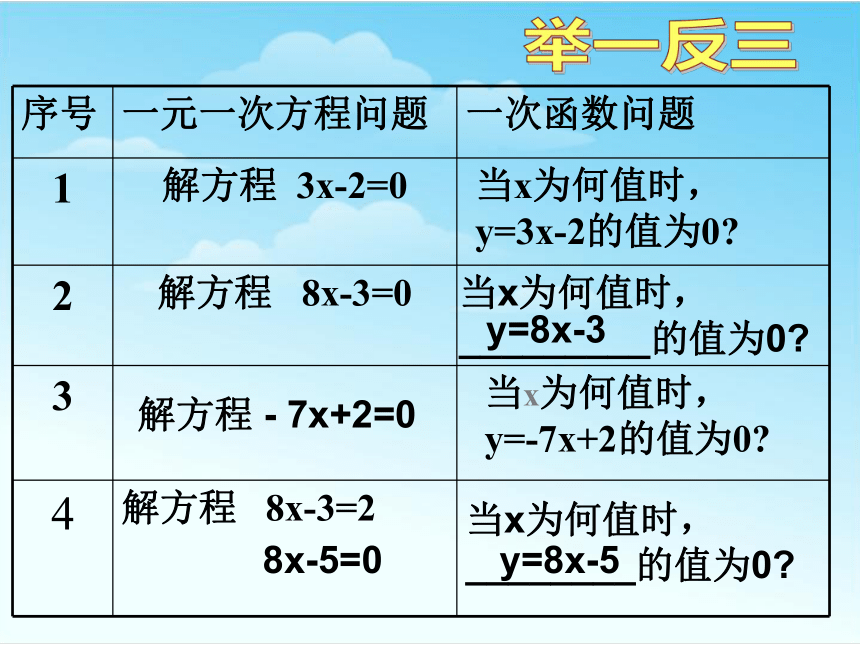
一元一次方程问题 一次函数问题 一次函数图象问题
解:函数 y=3x-6 的图象如图, 从函数图象上看,直线 y=3x-6 与 x 轴的交点坐标是(2,0),所以方程 3x-6=0 的解
是 x=2.
函数 y=3x-6 的图象如图,并根据图象回答方程 3x-6=0 的解是什么.
当x为何值时,_________的值为0?
解方程 - 7x+2=0
8x-5=0
y=8x-3
当x为何值时,________的值为0?
y=8x-5
序号 一元一次方程问题 一次函数问题
1 解方程 3x-2=0 当x为何值时,
y=3x-2的值为0?
2 解方程 8x-3=0
3 当x为何值时,
y=-7x+2的值为0?
4 解方程 8x-3=2
2.根据图象你能写出哪些一元一次方程的解
方程5x =0的解是x=0
方程x+2 =0的解是x=-2
方程-2.5x+5 =0的解是x=2
方程x-3 =0的解是x=3
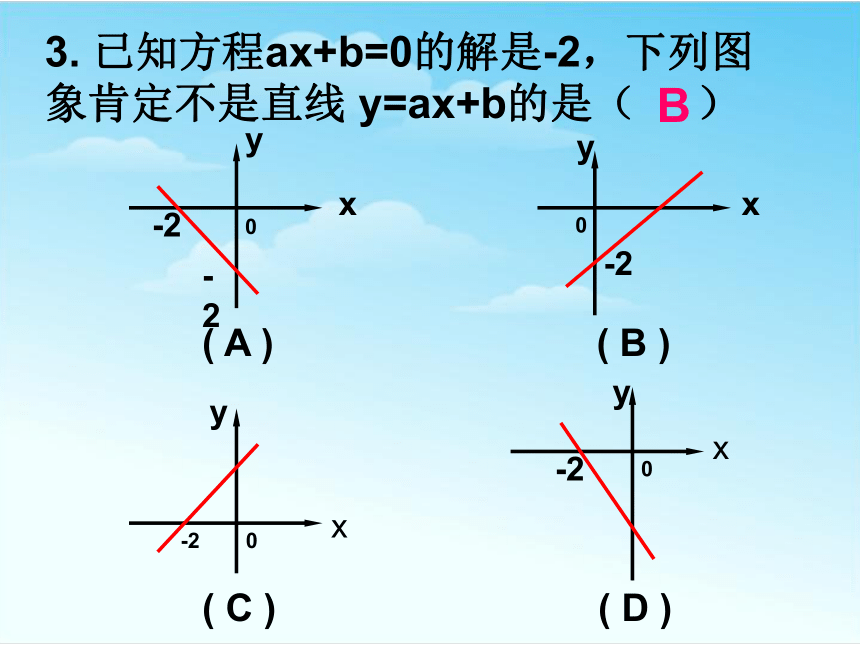
3. 已知方程ax+b=0的解是-2,下列图象肯定不是直线 y=ax+b的是( )
B
下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
思考
一次函数与一元一次方程
上面的三个方程可以看成函数y=2x+1的函数值分别为3,0,-1的情况,而这三个方程的解则分别对应着此时自变量的值,即图象上A,B,C三点的横坐标.
(1)2x+1=3;
(2)2x+1=0;
(3)2x+1=-1.
一次函数与一元一次方程
对于任意一个一元一次方程ax+b=0(a≠0),它有唯一解,我们可以把这个方程的解看成函数y=ax+b当y=0时与之对应的自变量的值.
从图象上看,方程的解是函数图象与x轴交点的横坐标.
下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
解一元一次方程 ax +b =k 就是求当函数值为k 时对应的自变量的值.
思考
用函数值的角度看:
下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
解一元一次方程
ax +b =k 就是确定直线y=ax +b与直线y=k的交点的横坐标.
思考
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
用函数图象的角度看:
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
思考
一次函数与一元一次不等式
三个不等式的左边都是代数式 ,而右边分别是2,0,-1.它们可以分别看成一次函数y=3x+2当y>2,y<0,y小于1 时自变量x的取值范围(如右图).
(1)3x+2>2;
(2)3x+2<0;
(3)3x+2<-1.
一次函数与一元一次不等式
对于任意一个一元一次不等式ax+b>0(a≠0),我们可以把这个不等式的解集看成函数y=ax+b当y>0时自变量x的取值范围.
不等式ax+b>0(a≠0)的解集是函数y=ax+b的图象在x轴上方的部分所对应的x的取值范围.
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
思考
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围.
用函数值的角度看:
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
思考
不等式ax+b>c的解集就是
使直线y =ax+b 在直线y=c上方时对应的自变量的取值范围;
不等式ax+b<c的解集就是
使直线y =ax+b 在直线y=c下方时对应的自变量的取值范围.
.
y =3x+2
y =2
y =0
y =-1
用函数图象的角度看:
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以
0.5 m/min 的速度上升.两个气球都上升了1 h.
请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
问题
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
二元一次方程与一次函数有
什么关系?
一次函数
二元一次方程
分析问题
从式子(数)角度看:
分析问题
在坐标系中画出以方程 y =0.5x+15 的解为坐标的点组成的图形就是一次函数y =0.5x+15 的图象.
从形的角度看,二元一次方程与一次函数有什么关
系?
分析问题
从形的角度看:
二元一次方程与一次函数的关系
解决问题
以数对(x,y) 为坐标画点
点的坐标满 足的方程
点的坐标满足 的函数关系
用方程观点看
用函数观点看
二元一次方程 y -0.5x =15
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以
0.5 m/min 的速度上升.两个气球都上升了1 h.
问题
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
从数(方程组)的角度看:
问题
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
大家会从数和形加以研究吗?
从数(函数值)的角度看:
就是求自变量为何值时,两个
一次函数 y =x+5,y =0.5x+15 的函
数值相等,并求出函数值.
问题
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
大家会从数和形加以研究吗?
就是求两个一次函数图象的交点坐标.
问题
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从形的角度看:
已知一次函数y=3x+5与y=2x+b的图象交点为(-1,2),
则方程组 的解是_______,b的值为______.
想一想
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
想一想
练习
1.利用函数图象解方程5x-3=x+2.
2.利用函数图象解不等式5x-1>2x+5.
3.当自变量x取何值时,函数y=2.5x+1和y=5x +17的值相等?这个函数值是多少?
3.当自变量x取何值时,函数y=2.5x+1和y=5x +17的值相等?这个函数值是多少?
方法一 :联立两个函数,得 2.5x+1=5x +17,解此方程;
方法二: 把两个函数转化为二元一次方程组,解方程组;
方法三: 画函数图象,求交点坐标.
如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求
直线l1与l2的解析式,
进而通过方程组求出交点坐标.
(1)请用函数的观点,从数形两方面说说你对二元一
次方程有什么新的理解;
(2)请用函数观点,从数和形两个角度说说对二元一
次方程组的认识;
(3)请用函数的观点,说说你对一元一次方程有什么
新的认识;
(4)请用函数的观点,说说一次函数与一元一次不等
式的联系.
课堂小结
本节课你有什么收获?
1.知识技能:方程的解 直线上点的坐标, 方程组的解 直线交点的坐标.
2.思想方法:转化思想、数形结合思想.
3.情感态度:经历画函数图象的过程,培养在动手实践中获得基本活动经验的研究意识,体会数形结合思想,感悟普遍联系观点.
五、课堂小结,共同提高
作业:教科书第99~100页第8,10,11,13 题.
课后作业
八年级 下册
19.2.3 一次函数与方程、不等式
本课是在学习一次函数的基础上,讨论一次函数与
二元一次方程的关系,用函数的观点看一元一次方
程、一元一次不等式、二元一次方程组.从而建立
它们之间的联系.
课件说明
课件说明
学习目标:
1.认识一次函数与一元(二元)一次方程(组)、
一元一次不等式之间的联系.会用函数观点解释
方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进
一步体会“以形表示数,以数解释形”的数形结
合思想.
学习重点:
理解一次函数与二元一次方程(组)的联系.
问题①:解方程2x+20=0
问题②:当x为何值时,函数y=2x+20的值0?
问题③:画出函数y=2x+20的图象,并确定
它与x轴的交点坐标;
问题④:问题① ②有何关系? ① ③呢?
x=-10
当x=-10时,函数y=2x+20的值0.
问题①:解方程2x+20=0
问题②:当x为何值时,函数y=2x+20的值0?
问题③:画出函数y=2x+20
的图象,并确定
它与x轴的交点坐标;
问题④:问题① ②有何关系? ① ③呢?
问题①与问题②可以看作是同一个问题两种形式.
问题① ②是从数的角度看,问题③是从图形的角度看.
直线y=2x+20与x轴的交点坐标为(-10,0)
1、方程ax+b=0(a、b为常数a≠0)的解是 .
2、当x 时,一次函数y= ax+b( a≠0)的值0?
3、直线y= ax+b 与x轴的交点坐标是 .
归纳
任何一个一元一次方程都可化为ax+b=0(a、b为常数,a≠0)的形式,所以解一元一次方程ax+b=0可转化为“当一次函数y=ax+b值为0时,求相应的自变量x的值.”
从图象上看,这又相当于“求直线y= ax+b 与x轴的交点的横坐标的值”
解方程
ax+b=0
求当x为何值时,
一次函数y=ax +b的值为0?
求函数y=ax +b
的图象与x轴交点
的横坐标的值
一元一次方程问题 一次函数问题 一次函数图象问题
解:函数 y=3x-6 的图象如图, 从函数图象上看,直线 y=3x-6 与 x 轴的交点坐标是(2,0),所以方程 3x-6=0 的解
是 x=2.
函数 y=3x-6 的图象如图,并根据图象回答方程 3x-6=0 的解是什么.
当x为何值时,_________的值为0?
解方程 - 7x+2=0
8x-5=0
y=8x-3
当x为何值时,________的值为0?
y=8x-5
序号 一元一次方程问题 一次函数问题
1 解方程 3x-2=0 当x为何值时,
y=3x-2的值为0?
2 解方程 8x-3=0
3 当x为何值时,
y=-7x+2的值为0?
4 解方程 8x-3=2
2.根据图象你能写出哪些一元一次方程的解
方程5x =0的解是x=0
方程x+2 =0的解是x=-2
方程-2.5x+5 =0的解是x=2
方程x-3 =0的解是x=3
3. 已知方程ax+b=0的解是-2,下列图象肯定不是直线 y=ax+b的是( )
B
下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
思考
一次函数与一元一次方程
上面的三个方程可以看成函数y=2x+1的函数值分别为3,0,-1的情况,而这三个方程的解则分别对应着此时自变量的值,即图象上A,B,C三点的横坐标.
(1)2x+1=3;
(2)2x+1=0;
(3)2x+1=-1.
一次函数与一元一次方程
对于任意一个一元一次方程ax+b=0(a≠0),它有唯一解,我们可以把这个方程的解看成函数y=ax+b当y=0时与之对应的自变量的值.
从图象上看,方程的解是函数图象与x轴交点的横坐标.
下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
解一元一次方程 ax +b =k 就是求当函数值为k 时对应的自变量的值.
思考
用函数值的角度看:
下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
解一元一次方程
ax +b =k 就是确定直线y=ax +b与直线y=k的交点的横坐标.
思考
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
用函数图象的角度看:
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
思考
一次函数与一元一次不等式
三个不等式的左边都是代数式 ,而右边分别是2,0,-1.它们可以分别看成一次函数y=3x+2当y>2,y<0,y小于1 时自变量x的取值范围(如右图).
(1)3x+2>2;
(2)3x+2<0;
(3)3x+2<-1.
一次函数与一元一次不等式
对于任意一个一元一次不等式ax+b>0(a≠0),我们可以把这个不等式的解集看成函数y=ax+b当y>0时自变量x的取值范围.
不等式ax+b>0(a≠0)的解集是函数y=ax+b的图象在x轴上方的部分所对应的x的取值范围.
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
思考
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围.
用函数值的角度看:
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
思考
不等式ax+b>c的解集就是
使直线y =ax+b 在直线y=c上方时对应的自变量的取值范围;
不等式ax+b<c的解集就是
使直线y =ax+b 在直线y=c下方时对应的自变量的取值范围.
.
y =3x+2
y =2
y =0
y =-1
用函数图象的角度看:
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以
0.5 m/min 的速度上升.两个气球都上升了1 h.
请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
问题
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
二元一次方程与一次函数有
什么关系?
一次函数
二元一次方程
分析问题
从式子(数)角度看:
分析问题
在坐标系中画出以方程 y =0.5x+15 的解为坐标的点组成的图形就是一次函数y =0.5x+15 的图象.
从形的角度看,二元一次方程与一次函数有什么关
系?
分析问题
从形的角度看:
二元一次方程与一次函数的关系
解决问题
以数对(x,y) 为坐标画点
点的坐标满 足的方程
点的坐标满足 的函数关系
用方程观点看
用函数观点看
二元一次方程 y -0.5x =15
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以
0.5 m/min 的速度上升.两个气球都上升了1 h.
问题
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
从数(方程组)的角度看:
问题
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
大家会从数和形加以研究吗?
从数(函数值)的角度看:
就是求自变量为何值时,两个
一次函数 y =x+5,y =0.5x+15 的函
数值相等,并求出函数值.
问题
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
大家会从数和形加以研究吗?
就是求两个一次函数图象的交点坐标.
问题
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从形的角度看:
已知一次函数y=3x+5与y=2x+b的图象交点为(-1,2),
则方程组 的解是_______,b的值为______.
想一想
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
想一想
练习
1.利用函数图象解方程5x-3=x+2.
2.利用函数图象解不等式5x-1>2x+5.
3.当自变量x取何值时,函数y=2.5x+1和y=5x +17的值相等?这个函数值是多少?
3.当自变量x取何值时,函数y=2.5x+1和y=5x +17的值相等?这个函数值是多少?
方法一 :联立两个函数,得 2.5x+1=5x +17,解此方程;
方法二: 把两个函数转化为二元一次方程组,解方程组;
方法三: 画函数图象,求交点坐标.
如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求
直线l1与l2的解析式,
进而通过方程组求出交点坐标.
(1)请用函数的观点,从数形两方面说说你对二元一
次方程有什么新的理解;
(2)请用函数观点,从数和形两个角度说说对二元一
次方程组的认识;
(3)请用函数的观点,说说你对一元一次方程有什么
新的认识;
(4)请用函数的观点,说说一次函数与一元一次不等
式的联系.
课堂小结
本节课你有什么收获?
1.知识技能:方程的解 直线上点的坐标, 方程组的解 直线交点的坐标.
2.思想方法:转化思想、数形结合思想.
3.情感态度:经历画函数图象的过程,培养在动手实践中获得基本活动经验的研究意识,体会数形结合思想,感悟普遍联系观点.
五、课堂小结,共同提高
作业:教科书第99~100页第8,10,11,13 题.
课后作业
