沪科版数学七年级下册10.2 《平行线的判定方法2、3》课件(共20张PPT)
文档属性
| 名称 | 沪科版数学七年级下册10.2 《平行线的判定方法2、3》课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 983.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
平行线的判定
-------方法2方法3
温故知新
1.判定两条直线平行的第一种方法是什么?
2.如图,直线c与直线a、b相交,∠1=48°,当∠4等于多少度时,直线a与b平行?
c
a
3
1
4
b
2
如图,举世闻名的三星堆考古中发掘出的一个类似梯形残缺玉片,工作人员估测玉片的上下边平行,你能帮助工作人员说明估测是否正确的吗?
A
D
B
C
抛砖引玉
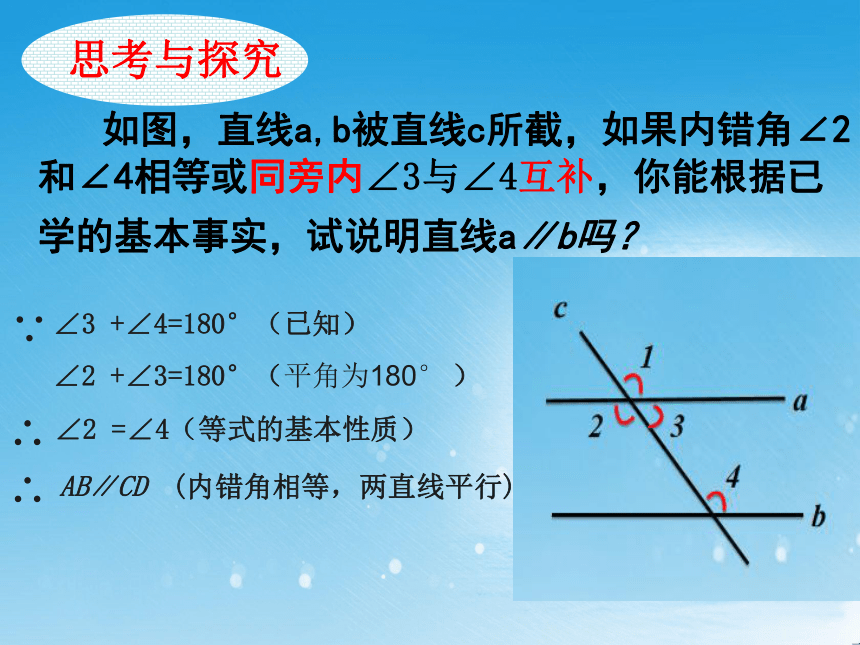
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等或同旁内∠3和∠4互补,你能根据已学的基本事实,试说明直线a∥b吗?
c
a
3
1
4
b
2
思考与探究
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等或同旁内∠3与∠4互补,你能根据已学的基本事实,试说明直线a∥b吗?
思考与探究
?
∠2 =∠4(已知)
∠1 =∠2(对顶角相等)
?
∠1 =∠4(等式的基本性质)
?
AB∥CD
(同位角相等,两直线平行)
b
两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.
平行线的判定方法2
简单说成:内错角相等,两直线平行.
(内错角相等,两直线平行)
?
∠1=∠2(已知)
?
AB∥CD.
几何语言:
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等或同旁内∠3与∠4互补,你能根据已学的基本事实,试说明直线a∥b吗?
?
∠3 +∠4=180°(已知)
∠2 +∠3=180°(平角为180° )
?
∠2 =∠4(等式的基本性质)
?
AB∥CD
(内错角相等,两直线平行)
思考与探究
两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
(同旁内角互补,两直线平行)
?
∠1+∠2=180°(已知)
?
AB∥CD
几何语言:
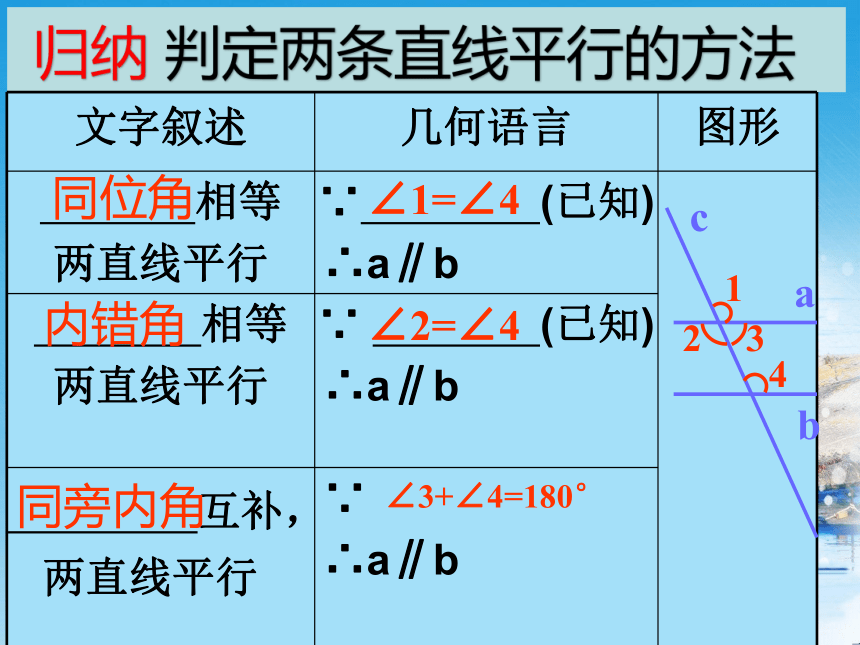
归纳 判定两条直线平行的方法
文字叙述 几何语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
同位角
内错角
同旁内角
∠1=∠4
∠2=∠4
∠3+∠4=180°
a
b
c
1
4
2
3
如图,举世闻名的三星堆考古中发掘出的一个类似梯形残缺玉片,工作人员估测玉片的上下边平行,你能帮助工作人员说明估测是否正确的吗?
A
D
B
C
学以致用
小试牛刀:如图,已知∠1=30°,
(1)∠2等于多少度时,则直线a//b?
(2)∠3等于多少度时,则直线a//b?
解:(1)∠2=30°
(2)∠3=150°
从∠1=∠4,可以推出 ∥ ,
理由是 。
(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。
A
B
C
D
1
2
3
4
5
例题讲解
AB
内错角相等,两直线平行
CD
2
3
内错角相等,两直线平行
如图
5
ADC
(3)从∠ABC +∠ =180 ° ,可以推出
AB∥CD ,理由是 。
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。
例题讲解
BCD
同旁内角互补,两直线平行
ABC
同位角相等,两直线平行
如图
A
B
C
D
1
2
3
4
5
1.如图,如果∠1=47°, ∠2=47°, ∠3=47°,可以判定哪些直线平行?请说明理由。
∵ ∠1=47°,∠2=47°(已知) ∴ ∠1=∠2(等式的基本性质)
∴DE∥BC
(内错角相等,两直线平行)
理解运用
解:DE∥BC、AB∥EF
1.如图,如果∠1=47°, ∠2=47°, ∠3=47°,可以判定哪些直线平行?请说明理由。
∵ ∠2=47°,∠3=47°(已知) ∴ ∠2=∠3 (等式的基本性质)
∴AB∥EF
(同位角相等,两直线平行)
理解运用
解:
2.如图,若∠A=62°, ∠B=118°,可以判定哪两条直线平行?判定的依据是什么?
∵ ∠A=62°∠B=118°(已知)
∴∠A+∠B=180°(等式基本性质)
∴ AD∥BC
(同旁内角互补,两直线平行)
理解运用
解: AD∥BC
(同旁内角互补,两直线平行)
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
位置关系+数量关系
位置关系(平行)
小结
本节课你还有哪些收获,请同大家分享?
著名数学家陈景润:
学习要有三心,一信心,二决心,三恒心。
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出 ∥ ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。
必做题
4
2
c
d
3
1
a
b
1.如图
如图,根据下列条件可判断哪两条直线平行,并说明理由。
(1)∠1=∠2
(2)∠3=∠A
(3)∠A+∠2+∠4=180°
预习:平行线的性质
选做题
平行线的判定
-------方法2方法3
温故知新
1.判定两条直线平行的第一种方法是什么?
2.如图,直线c与直线a、b相交,∠1=48°,当∠4等于多少度时,直线a与b平行?
c
a
3
1
4
b
2
如图,举世闻名的三星堆考古中发掘出的一个类似梯形残缺玉片,工作人员估测玉片的上下边平行,你能帮助工作人员说明估测是否正确的吗?
A
D
B
C
抛砖引玉
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等或同旁内∠3和∠4互补,你能根据已学的基本事实,试说明直线a∥b吗?
c
a
3
1
4
b
2
思考与探究
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等或同旁内∠3与∠4互补,你能根据已学的基本事实,试说明直线a∥b吗?
思考与探究
?
∠2 =∠4(已知)
∠1 =∠2(对顶角相等)
?
∠1 =∠4(等式的基本性质)
?
AB∥CD
(同位角相等,两直线平行)
b
两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.
平行线的判定方法2
简单说成:内错角相等,两直线平行.
(内错角相等,两直线平行)
?
∠1=∠2(已知)
?
AB∥CD.
几何语言:
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等或同旁内∠3与∠4互补,你能根据已学的基本事实,试说明直线a∥b吗?
?
∠3 +∠4=180°(已知)
∠2 +∠3=180°(平角为180° )
?
∠2 =∠4(等式的基本性质)
?
AB∥CD
(内错角相等,两直线平行)
思考与探究
两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
(同旁内角互补,两直线平行)
?
∠1+∠2=180°(已知)
?
AB∥CD
几何语言:
归纳 判定两条直线平行的方法
文字叙述 几何语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
同位角
内错角
同旁内角
∠1=∠4
∠2=∠4
∠3+∠4=180°
a
b
c
1
4
2
3
如图,举世闻名的三星堆考古中发掘出的一个类似梯形残缺玉片,工作人员估测玉片的上下边平行,你能帮助工作人员说明估测是否正确的吗?
A
D
B
C
学以致用
小试牛刀:如图,已知∠1=30°,
(1)∠2等于多少度时,则直线a//b?
(2)∠3等于多少度时,则直线a//b?
解:(1)∠2=30°
(2)∠3=150°
从∠1=∠4,可以推出 ∥ ,
理由是 。
(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。
A
B
C
D
1
2
3
4
5
例题讲解
AB
内错角相等,两直线平行
CD
2
3
内错角相等,两直线平行
如图
5
ADC
(3)从∠ABC +∠ =180 ° ,可以推出
AB∥CD ,理由是 。
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。
例题讲解
BCD
同旁内角互补,两直线平行
ABC
同位角相等,两直线平行
如图
A
B
C
D
1
2
3
4
5
1.如图,如果∠1=47°, ∠2=47°, ∠3=47°,可以判定哪些直线平行?请说明理由。
∵ ∠1=47°,∠2=47°(已知) ∴ ∠1=∠2(等式的基本性质)
∴DE∥BC
(内错角相等,两直线平行)
理解运用
解:DE∥BC、AB∥EF
1.如图,如果∠1=47°, ∠2=47°, ∠3=47°,可以判定哪些直线平行?请说明理由。
∵ ∠2=47°,∠3=47°(已知) ∴ ∠2=∠3 (等式的基本性质)
∴AB∥EF
(同位角相等,两直线平行)
理解运用
解:
2.如图,若∠A=62°, ∠B=118°,可以判定哪两条直线平行?判定的依据是什么?
∵ ∠A=62°∠B=118°(已知)
∴∠A+∠B=180°(等式基本性质)
∴ AD∥BC
(同旁内角互补,两直线平行)
理解运用
解: AD∥BC
(同旁内角互补,两直线平行)
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
位置关系+数量关系
位置关系(平行)
小结
本节课你还有哪些收获,请同大家分享?
著名数学家陈景润:
学习要有三心,一信心,二决心,三恒心。
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出 ∥ ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。
必做题
4
2
c
d
3
1
a
b
1.如图
如图,根据下列条件可判断哪两条直线平行,并说明理由。
(1)∠1=∠2
(2)∠3=∠A
(3)∠A+∠2+∠4=180°
预习:平行线的性质
选做题
