人教版七年级下册数学课件 :6.1算术平方根的定义 (共35张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件 :6.1算术平方根的定义 (共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
初一年级 数学
算术平方根的定义
, ,其中g是物理中的一个常数(重力加速度) , ,
你们知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围内吗?
这时它的速度要大于第一宇宙速度v1(单位:m/s)而小于第二宇宙速度v2 (单位:m/s). v1 , v2的大小满足
R是地球半径,
随着对于数的认识的不断深入,人们发现,边长为1的正方形的对角线的长不是有理数,这就需要引入一种新的数——无理数.
本章将首先学习平方根与立方根;在此基础上引入无理数,把数的范围扩充到实数;然后类比有理数,引入实数在数轴上的表示和实数的运算,并用这些知识解决一些实际问题.
算术平方根的定义
第六章 实数
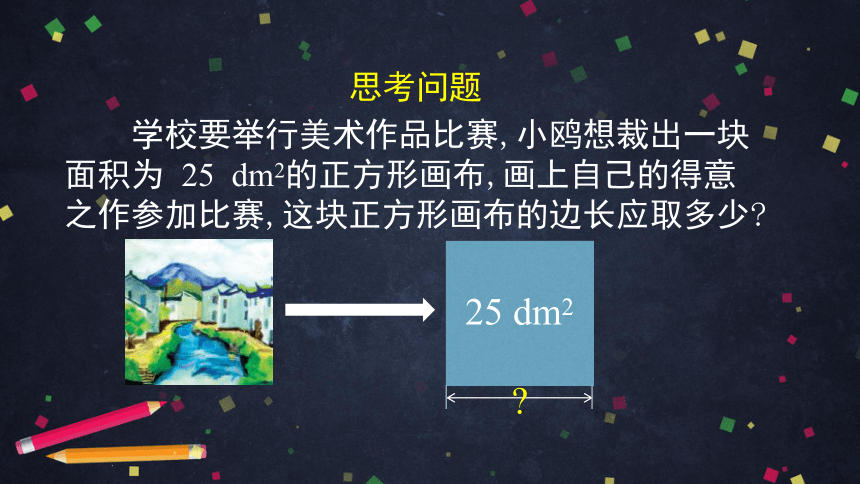
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
思考问题
25 dm2
25 dm2
因为 52 = 25,所以这个正方形的边长应取? 5 dm.
思考问题
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
所以,这个正方形画布的边长应取 5 dm.
思考问题
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
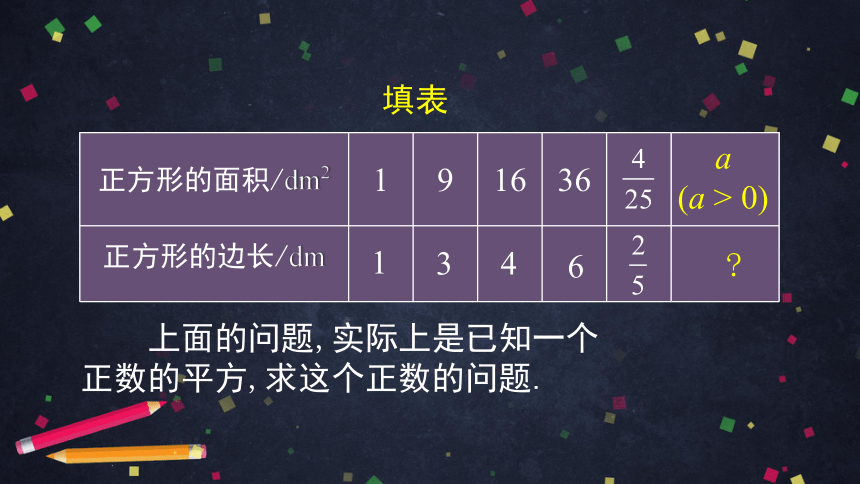
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
?
a
(a > 0)
分析:设正方形的边长为 x dm
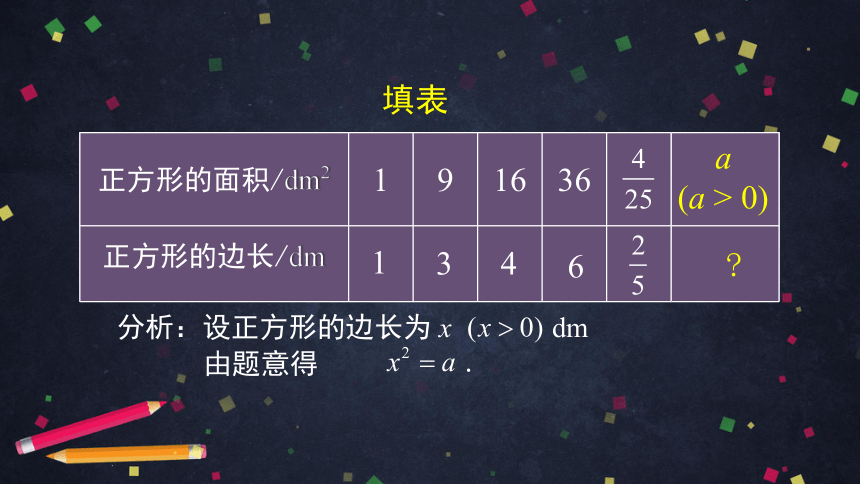
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
由题意得
.
?
a
(a > 0)
如:32 = 9 ,所以 9 的算术平方根是 3;即 .
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
算术平方根的定义
算术平方根的定义
由上述定义可得:
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
算术平方根的定义
由上述定义可得:
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
由算术平方根的意义可知
?
分析:设正方形的边长为 x dm
由题意得
.
a
(a > 0)
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
a
(a > 0)
由算术平方根的意义可知
分析:设正方形的边长为 x dm
由题意得
.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
2
由算术平方根的意义可知
分析:设正方形的边长为 x dm
由题意得
.
典型例题
判断下列说法是否正确:
52=25
正确
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
典型例题
判断下列说法是否正确:
算术平方根是非负数.
正确
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
典型例题
判断下列说法是否正确:
因为0.12=0.01;
所以
正确
错误
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
典型例题
判断下列说法是否正确:
被开方数是非负数.
正确
错误
错误
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0的算术平方根是0.
由上述定义可得:
(1)因为102 = 100,所以100的算术平方根是10,即 ;
(2)因为 ,所以 的算术平方根是 ,即 ;
(3)因为0.012 = 0.0001,所以0.0001的算术平方根是 0.01 ,即 .
(1) 100 ; (2) (3) 0.0001 .
解:
求下列各数的算术平方根:
典型例题
典型例题
可以看出:
, ;
被开方数越大,对应的算术平方根也越大.
这个结论对所有正数都成立.
; ; .
(1) 100 ; (2) (3) 0.0001 .
解:
求下列各数的算术平方根:
解:
(1)因为 92 = 81,所以 81 的算术平方根是 9,即 ;
(2)因为 ,所以 的算术平方根是 ,
即 ;
典型例题
求下列各式的值:
典型例题
(3)因为 62 = 36,所以 ;
解:
因为 62 = 36,所以36的算术平方根是 6,即 ;
所以 ;
求下列各式的值:
(4)因为 ,所以 ;
典型例题
解:
因为 ,所以25的算术平方根是5,即 ;
所以 .
求下列各式的值:
小结
正确依据算术平方根的定义求一个非负数的算术平方根.
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0 .
巩固练习
答:
(1)无意义;
(4)有意义.
(2)有意义;
(3)有意义;
下列各式是否有意义?
(1)因为 0.22 = 0.04,所以0.04的算术平方根是0.2,即 ;
巩固练习
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
巩固练习
(2)因为 ,所以 的算术平方根是 ,
即 ;
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
巩固练习
即 ;所以 102 的算术平方根是10,
即
(3)因为 102 = 100,所以 ;
因为 102 = 100,所以100的算术平方根是10,
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
巩固练习
所以 的算术平方根是 2 .
(4)因为 42 = 16,所以 16 的算术平方根是 4 ,即 ;
所以 的算术平方根就是4的算术平方根;
因为 22 = 4,所以 4 的算术平方根是 2 ,即 ;
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
物体自由下落的高度 h(单位:m)与下落时间 t(单位:s)的关系是 h = 4.9 t2.有一个物体从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将 h = 19.6 代入到关系式 h = 4.9 t2,得
19.6 = 4.9t2 ;
t2 = 4 ;
因为 t 是非负数,所有 t = = 2(s) .
巩固练习
课堂小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定: 0 的算术平方根是 0.
依据算术平方根的定义,可求得某一个非负数的算术平方根.
由算术平方根的定义,
得
课后作业
1. 求下列各数的算术平方根:
(1) 0.0025; (2) 81 ; (3) .
2. 求下列各式的值:
;
;
同学们再见!
初一年级 数学
算术平方根的定义
, ,其中g是物理中的一个常数(重力加速度) , ,
你们知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围内吗?
这时它的速度要大于第一宇宙速度v1(单位:m/s)而小于第二宇宙速度v2 (单位:m/s). v1 , v2的大小满足
R是地球半径,
随着对于数的认识的不断深入,人们发现,边长为1的正方形的对角线的长不是有理数,这就需要引入一种新的数——无理数.
本章将首先学习平方根与立方根;在此基础上引入无理数,把数的范围扩充到实数;然后类比有理数,引入实数在数轴上的表示和实数的运算,并用这些知识解决一些实际问题.
算术平方根的定义
第六章 实数
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
思考问题
25 dm2
25 dm2
因为 52 = 25,所以这个正方形的边长应取? 5 dm.
思考问题
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
所以,这个正方形画布的边长应取 5 dm.
思考问题
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
?
a
(a > 0)
分析:设正方形的边长为 x dm
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
由题意得
.
?
a
(a > 0)
如:32 = 9 ,所以 9 的算术平方根是 3;即 .
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
算术平方根的定义
算术平方根的定义
由上述定义可得:
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
算术平方根的定义
由上述定义可得:
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
由算术平方根的意义可知
?
分析:设正方形的边长为 x dm
由题意得
.
a
(a > 0)
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
a
(a > 0)
由算术平方根的意义可知
分析:设正方形的边长为 x dm
由题意得
.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
2
由算术平方根的意义可知
分析:设正方形的边长为 x dm
由题意得
.
典型例题
判断下列说法是否正确:
52=25
正确
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
典型例题
判断下列说法是否正确:
算术平方根是非负数.
正确
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
典型例题
判断下列说法是否正确:
因为0.12=0.01;
所以
正确
错误
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
典型例题
判断下列说法是否正确:
被开方数是非负数.
正确
错误
错误
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0的算术平方根是0.
由上述定义可得:
(1)因为102 = 100,所以100的算术平方根是10,即 ;
(2)因为 ,所以 的算术平方根是 ,即 ;
(3)因为0.012 = 0.0001,所以0.0001的算术平方根是 0.01 ,即 .
(1) 100 ; (2) (3) 0.0001 .
解:
求下列各数的算术平方根:
典型例题
典型例题
可以看出:
, ;
被开方数越大,对应的算术平方根也越大.
这个结论对所有正数都成立.
; ; .
(1) 100 ; (2) (3) 0.0001 .
解:
求下列各数的算术平方根:
解:
(1)因为 92 = 81,所以 81 的算术平方根是 9,即 ;
(2)因为 ,所以 的算术平方根是 ,
即 ;
典型例题
求下列各式的值:
典型例题
(3)因为 62 = 36,所以 ;
解:
因为 62 = 36,所以36的算术平方根是 6,即 ;
所以 ;
求下列各式的值:
(4)因为 ,所以 ;
典型例题
解:
因为 ,所以25的算术平方根是5,即 ;
所以 .
求下列各式的值:
小结
正确依据算术平方根的定义求一个非负数的算术平方根.
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0 .
巩固练习
答:
(1)无意义;
(4)有意义.
(2)有意义;
(3)有意义;
下列各式是否有意义?
(1)因为 0.22 = 0.04,所以0.04的算术平方根是0.2,即 ;
巩固练习
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
巩固练习
(2)因为 ,所以 的算术平方根是 ,
即 ;
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
巩固练习
即 ;所以 102 的算术平方根是10,
即
(3)因为 102 = 100,所以 ;
因为 102 = 100,所以100的算术平方根是10,
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
巩固练习
所以 的算术平方根是 2 .
(4)因为 42 = 16,所以 16 的算术平方根是 4 ,即 ;
所以 的算术平方根就是4的算术平方根;
因为 22 = 4,所以 4 的算术平方根是 2 ,即 ;
解:
(1) 0.04 ; (2) ; (3) 102 ; (4) .
求下列各数的算术平方根:
物体自由下落的高度 h(单位:m)与下落时间 t(单位:s)的关系是 h = 4.9 t2.有一个物体从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将 h = 19.6 代入到关系式 h = 4.9 t2,得
19.6 = 4.9t2 ;
t2 = 4 ;
因为 t 是非负数,所有 t = = 2(s) .
巩固练习
课堂小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做? a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定: 0 的算术平方根是 0.
依据算术平方根的定义,可求得某一个非负数的算术平方根.
由算术平方根的定义,
得
课后作业
1. 求下列各数的算术平方根:
(1) 0.0025; (2) 81 ; (3) .
2. 求下列各式的值:
;
;
同学们再见!
