北京版七年级下册数学课件:5.3 代入消元法解二元一次方程组 (共43张PPT)
文档属性
| 名称 | 北京版七年级下册数学课件:5.3 代入消元法解二元一次方程组 (共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
初一年级 数学
解二元一次方程组
观察题目特征选择合适的解法
知识回顾
1.解二元一次方程组的基本思路及基本方法.
二元一次方程组
消元转化思想
代入消元法
加减消元法
一元一次方程
知识回顾
2.代入消元法解二元一次方程组的步骤.
例如:用代入消元法解方程组
①
②
所以原方程组的解是
③
把③代入② ,得
①变形,得
解:
把 代入③ ,得
知识回顾
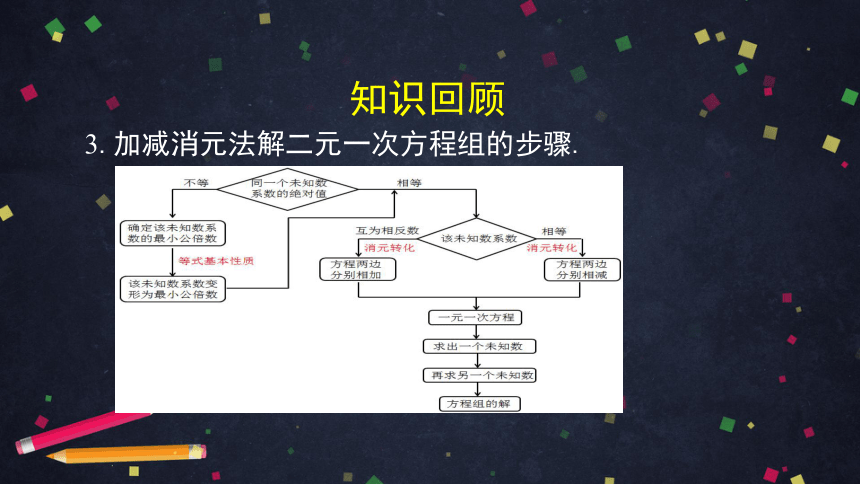
3.加减消元法解二元一次方程组的步骤.
例如:用加减消元法解方程组
①
②
所以原方程组的解是
③
①×3
解:
把 代入① ,得
,得
②×2
,得
④
③+④,得
1.下面有3个二元一次方程:
① ② ③
交流活动
(1)选择其中两个方程联立方程组,并用代入消元法
求解,说说你选择的理由.
甲同学做法:①与②联立方程组
乙同学做法:①与③联立方程组
丙同学做法:②与③联立方程组
你同意哪位同学的做法?
x的系数为1
变形
√
√
1.下面有3个二元一次方程
① ② ③
交流活动
1.下面有3个二元一次方程
① ② ③
交流活动
(1)选择其中两个方程联立方程组,并用代入消元法
求解,说说你选择的理由.
④
①与④;
答:①与②; ①与③;
②与④; ③与④.
1.下面有3个二元一次方程
① ② ③
交流活动
(2)选择其中两个方程联立方程组,并用加减消元法
求解,说说你选择的理由.
甲同学做法:①与②联立方程组
乙同学做法:①与③联立方程组
丙同学做法:②与③联立方程组
这次你同意谁的做法呢?
y的系数互为
相反数
(加法消元)
x的系数相等
(减法消元)
√
√
交流活动
甲同学联立的方程组:
x的系数为1;y的系数互为相反数.
题目特征:
选择你喜欢的消元方法求解!
交流活动
2.选择合适的方法解方程组
分析:方程组中未知数的系数不为±1,
同一个未知数的系数不具有互为相反数或相等的特征.
建议:分别用代入消元法和加减消元法求解,
再对比分析!
代入消元法解方程组
①
②
把③代入②,得
解:
①变形,得
③
①
②
①×2,得
②+③,得
③
解:
加减消元法解方程组
代入消元法:
加减消元法:
交流活动
2.选择合适的方法解方程组
小小结:方程组中未知数的系数不为±1,同一个未知数的系数不具有互为相反数或相等的特征,但某个未知数的系数有倍数关系时,加减消元法计算简便.
交流活动
3.选择合适的方法解方程组
系数与常数
项有公因数
观察:某个方程中未知数系数与常数项有什么关系?
①
②
3.选择合适的方法解方程组
①
②
①÷2,得
③变形,得
③
把④代入②,得
所以原方程组的解是
解:
④
把 代入④,得
①变形,得
交流活动
3.选择合适的方法解方程组
小小结:当方程组中未知数的系数不为±1,同一个未知数系数不具有互为相反数或相等的特征,也没有倍数关系,但某个方程中未知数系数和常数项有公因数时,应灵活运用等式的基本性质将该方程未知数系数化简,再选择合适的消元方法求解.
系数与常数
项有公因数
交流活动
4.选择合适的方法解方程组
分析:这个方程组中不具有前3道题归纳的特征.
建议:分别用代入消元法和加减消元法求解,再对比分析.
所以原方程组
的解是
代入消元法解:
①
②
①变形,得
③
把③代入②,得
解:
把 代入③,得
加减消元法解:
①
②
③
解:
把 代入①,得
①×2,得
③+④,得
④
②×5,得
所以原方程组
的解是
代入消元法
加减消元法
小小结:
解法 步骤数量 解题的计算量
代入法 基本相同 变形后有分母增加计算难度
加减法 计算相对简单,要注意减法消元的易错点.
4.选择合适的方法解方程组
结合自己的学习情况选择合适的方法即可.
方法小结
(1)
(2)
(3)
(4)
方法小结
(5)
(6)
①×3,得
①
②
③
④
②×2,得
结合自己的学习情况选择合适的方法即可.
典型例题
选择合适的方法解方程组
①
②
把 代入①,得
①-②,得
所以原方程组的解是
解:
x的系数为1;
x的系数相等.
典型例题
选择合适的方法解方程组
①
②
所以原方程组的解是
②变形,得
③
把③代入①,得
解:
把 代入③,得
y的系数为-1;
同一个未知数
的系数有倍数
关系.
典型例题
选择合适的方法解方程组
分析:y的系数有-5倍关系;
①
②
方程②的未知数系数和常数项有公因数5.
①×5.
②÷5.
典型例题
选择合适的方法解方程组
①
②
②÷5,得
③
解:
把 代入③,得
①+③,得
所以原方程组的解是
典型例题
选择合适的方法解方程组
①
②
分析:同一个未知数系数;
建议:用加减消元法求解,计算简便.
每个方程未知数系数和常数项.
均无上述特征.
典型例题
选择合适的方法解方程组
①
②
x的系数分别是13和7.
①×7;②×13.
y的系数分别为2和-3
①×3;②×2.
典型例题
选择合适的方法解方程组
①
②
②×2,得
③
解:
把 代入② ,得
③+④,得
所以原方程组
的解是
①×3,得
④
提升练习
由于粗心,在解方程组 时,小明把□系数抄错了,得到的解是 小亮把常数△抄错了,得到的解是
请你帮助他们纠正解题中的错误,写出□,△所代表的数,并求原方程组的解.
课堂小结
课堂小结
1.解二元一次方程组的基本思路与基本方法.
二元一次方程组
消元转化思想
代入消元法
加减消元法
一元一次方程
2.根据题目特征选择合适的消元方法.
某个未知数系数的特征 合适的解法
±1 代入消元
互为相反数或相等 加减消元
有倍数关系 加减消元
具有上述多种特征 自己喜欢的解法
(1)
(2)当方程中未知数系数和常数项有公因数时,先将该
方程化简,再决定选用哪种消元方法;
(3)当方程组不具备上述任何特征时,加减消元法计
算相对简便,但注意相减时的易错点.
课堂小结
2.根据题目特征选择合适的消元方法.
建议:结合自己的学习情况选择合适的方法.
1.选用适合的方法解下列方程组:
2. 已知关于x,y的二元一次方程组 的解
满足 ,试求a的取值范围.
课后作业
观察可能导致发现,观察将揭示某种规则、
模式或定律.
——波利亚
谢谢收看
同学们,再见!
初一年级 数学
解二元一次方程组
观察题目特征选择合适的解法
知识回顾
1.解二元一次方程组的基本思路及基本方法.
二元一次方程组
消元转化思想
代入消元法
加减消元法
一元一次方程
知识回顾
2.代入消元法解二元一次方程组的步骤.
例如:用代入消元法解方程组
①
②
所以原方程组的解是
③
把③代入② ,得
①变形,得
解:
把 代入③ ,得
知识回顾
3.加减消元法解二元一次方程组的步骤.
例如:用加减消元法解方程组
①
②
所以原方程组的解是
③
①×3
解:
把 代入① ,得
,得
②×2
,得
④
③+④,得
1.下面有3个二元一次方程:
① ② ③
交流活动
(1)选择其中两个方程联立方程组,并用代入消元法
求解,说说你选择的理由.
甲同学做法:①与②联立方程组
乙同学做法:①与③联立方程组
丙同学做法:②与③联立方程组
你同意哪位同学的做法?
x的系数为1
变形
√
√
1.下面有3个二元一次方程
① ② ③
交流活动
1.下面有3个二元一次方程
① ② ③
交流活动
(1)选择其中两个方程联立方程组,并用代入消元法
求解,说说你选择的理由.
④
①与④;
答:①与②; ①与③;
②与④; ③与④.
1.下面有3个二元一次方程
① ② ③
交流活动
(2)选择其中两个方程联立方程组,并用加减消元法
求解,说说你选择的理由.
甲同学做法:①与②联立方程组
乙同学做法:①与③联立方程组
丙同学做法:②与③联立方程组
这次你同意谁的做法呢?
y的系数互为
相反数
(加法消元)
x的系数相等
(减法消元)
√
√
交流活动
甲同学联立的方程组:
x的系数为1;y的系数互为相反数.
题目特征:
选择你喜欢的消元方法求解!
交流活动
2.选择合适的方法解方程组
分析:方程组中未知数的系数不为±1,
同一个未知数的系数不具有互为相反数或相等的特征.
建议:分别用代入消元法和加减消元法求解,
再对比分析!
代入消元法解方程组
①
②
把③代入②,得
解:
①变形,得
③
①
②
①×2,得
②+③,得
③
解:
加减消元法解方程组
代入消元法:
加减消元法:
交流活动
2.选择合适的方法解方程组
小小结:方程组中未知数的系数不为±1,同一个未知数的系数不具有互为相反数或相等的特征,但某个未知数的系数有倍数关系时,加减消元法计算简便.
交流活动
3.选择合适的方法解方程组
系数与常数
项有公因数
观察:某个方程中未知数系数与常数项有什么关系?
①
②
3.选择合适的方法解方程组
①
②
①÷2,得
③变形,得
③
把④代入②,得
所以原方程组的解是
解:
④
把 代入④,得
①变形,得
交流活动
3.选择合适的方法解方程组
小小结:当方程组中未知数的系数不为±1,同一个未知数系数不具有互为相反数或相等的特征,也没有倍数关系,但某个方程中未知数系数和常数项有公因数时,应灵活运用等式的基本性质将该方程未知数系数化简,再选择合适的消元方法求解.
系数与常数
项有公因数
交流活动
4.选择合适的方法解方程组
分析:这个方程组中不具有前3道题归纳的特征.
建议:分别用代入消元法和加减消元法求解,再对比分析.
所以原方程组
的解是
代入消元法解:
①
②
①变形,得
③
把③代入②,得
解:
把 代入③,得
加减消元法解:
①
②
③
解:
把 代入①,得
①×2,得
③+④,得
④
②×5,得
所以原方程组
的解是
代入消元法
加减消元法
小小结:
解法 步骤数量 解题的计算量
代入法 基本相同 变形后有分母增加计算难度
加减法 计算相对简单,要注意减法消元的易错点.
4.选择合适的方法解方程组
结合自己的学习情况选择合适的方法即可.
方法小结
(1)
(2)
(3)
(4)
方法小结
(5)
(6)
①×3,得
①
②
③
④
②×2,得
结合自己的学习情况选择合适的方法即可.
典型例题
选择合适的方法解方程组
①
②
把 代入①,得
①-②,得
所以原方程组的解是
解:
x的系数为1;
x的系数相等.
典型例题
选择合适的方法解方程组
①
②
所以原方程组的解是
②变形,得
③
把③代入①,得
解:
把 代入③,得
y的系数为-1;
同一个未知数
的系数有倍数
关系.
典型例题
选择合适的方法解方程组
分析:y的系数有-5倍关系;
①
②
方程②的未知数系数和常数项有公因数5.
①×5.
②÷5.
典型例题
选择合适的方法解方程组
①
②
②÷5,得
③
解:
把 代入③,得
①+③,得
所以原方程组的解是
典型例题
选择合适的方法解方程组
①
②
分析:同一个未知数系数;
建议:用加减消元法求解,计算简便.
每个方程未知数系数和常数项.
均无上述特征.
典型例题
选择合适的方法解方程组
①
②
x的系数分别是13和7.
①×7;②×13.
y的系数分别为2和-3
①×3;②×2.
典型例题
选择合适的方法解方程组
①
②
②×2,得
③
解:
把 代入② ,得
③+④,得
所以原方程组
的解是
①×3,得
④
提升练习
由于粗心,在解方程组 时,小明把□系数抄错了,得到的解是 小亮把常数△抄错了,得到的解是
请你帮助他们纠正解题中的错误,写出□,△所代表的数,并求原方程组的解.
课堂小结
课堂小结
1.解二元一次方程组的基本思路与基本方法.
二元一次方程组
消元转化思想
代入消元法
加减消元法
一元一次方程
2.根据题目特征选择合适的消元方法.
某个未知数系数的特征 合适的解法
±1 代入消元
互为相反数或相等 加减消元
有倍数关系 加减消元
具有上述多种特征 自己喜欢的解法
(1)
(2)当方程中未知数系数和常数项有公因数时,先将该
方程化简,再决定选用哪种消元方法;
(3)当方程组不具备上述任何特征时,加减消元法计
算相对简便,但注意相减时的易错点.
课堂小结
2.根据题目特征选择合适的消元方法.
建议:结合自己的学习情况选择合适的方法.
1.选用适合的方法解下列方程组:
2. 已知关于x,y的二元一次方程组 的解
满足 ,试求a的取值范围.
课后作业
观察可能导致发现,观察将揭示某种规则、
模式或定律.
——波利亚
谢谢收看
同学们,再见!
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
