江苏省高邮市阳光双语初中2019-2020学年度下期七年级数学期中复习导学案(有解析答案)
文档属性
| 名称 | 江苏省高邮市阳光双语初中2019-2020学年度下期七年级数学期中复习导学案(有解析答案) |  | |
| 格式 | zip | ||
| 文件大小 | 958.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 10:02:58 | ||
图片预览



文档简介
七年级下数学期中复习导学案
学习目标:复习巩固数学前三章重要知识点题型
一、专题精讲
专题一 计算
例1 化简计算
1、 2、
3、 4、
例2 因式分解
1、 2、
3、 4、
专题二 计算的应用
例1 化简求值:(3x+2)(3x-2)-5x(3x-2)+(2-3x)2,其中x=-.
巩固 已知:(x+a)(x-)的结果中不含关于字母的一次项,求的值
例2、我们学习了因式分解之后可以解某些高次方程,例如,一元二次方程x2+x-2=0可以通过因式分解化为:(x-1)(x+2)=0,则方程的两个解为x=1和x=-2.反之,如果x=1是某方程ax2+bx+c=0的一个解,则多项式ax2+bx+c必有一个因式是 (x-1),在理解上文的基础上,试找出多项式x3+x2-3x+1的一个因式,并将这个多项式因式分解.
专题三 平行
例1 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
巩固 小玲观察下图得出“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等”这个结论,你是否认同小玲的观点?如果认同,则给出证明;如果不认同,则画出所有可能的情况,猜想相应的结论,并给出证明.
例2、在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:
∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=∠ABC,(角的平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
专题三 平行中求面积
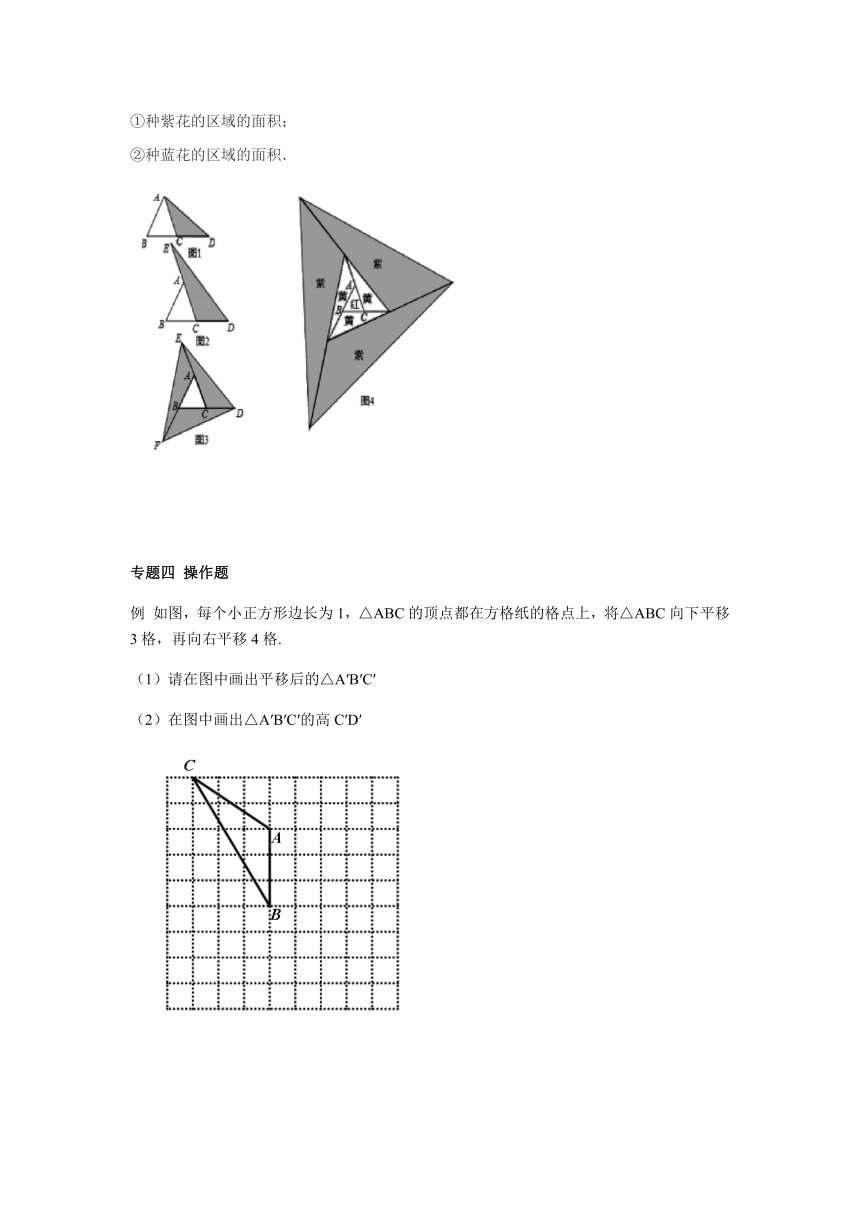
例1 (1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;
(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO的面积相等;
(3)如图3,点M在△ABC的边上, 过点M画一条平分三角形面积的直线.
巩固、
探索:在图1至图3中,已知△ABC的面积为a,
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1= (用含a的代数式表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2= (用含a的代数式表示)
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3= (用含a的代数式表示)
并运用上述(2)的结论写出理由.发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 .
应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
①种紫花的区域的面积;
②种蓝花的区域的面积.
专题四 操作题
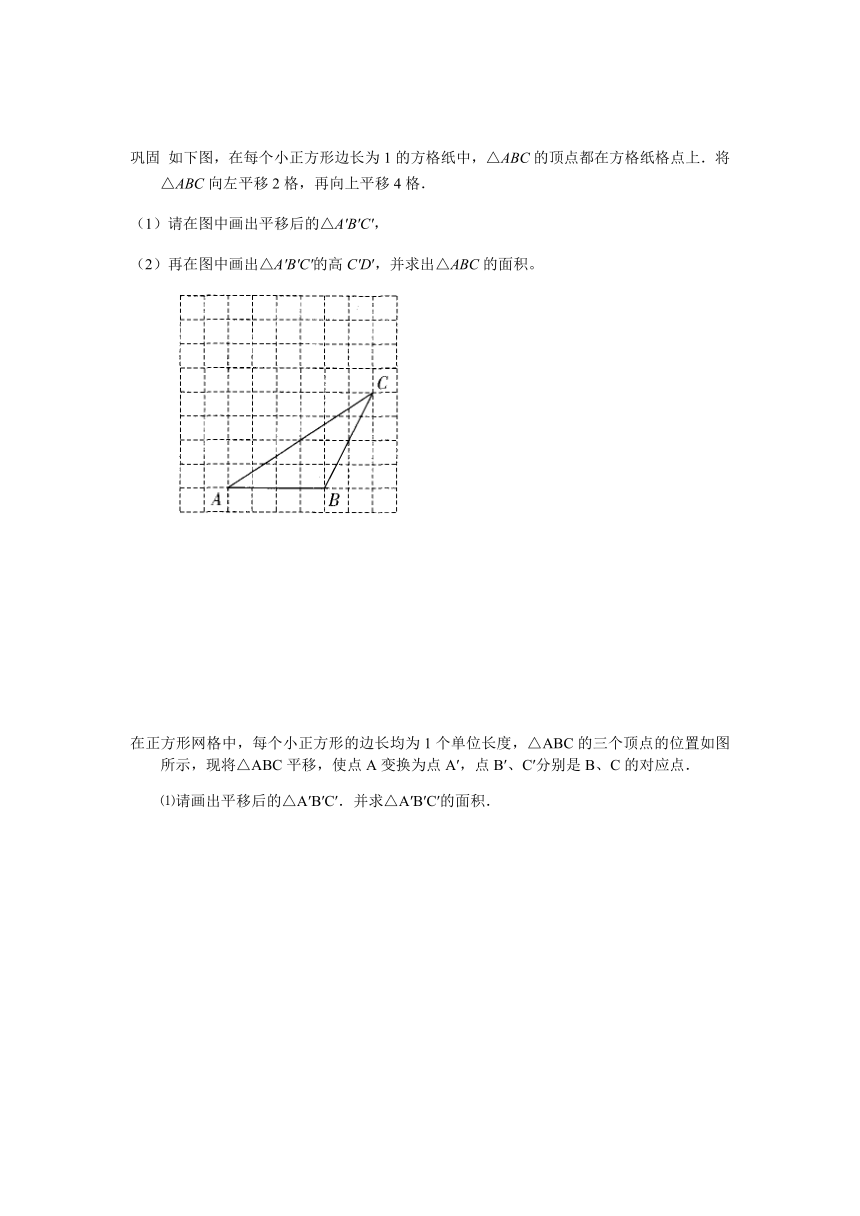
例 如图,每个小正方形边长为1,△ABC的顶点都在方格纸的格点上,将△ABC向下平移3格,再向右平移4格.
(1)请在图中画出平移后的△A′B′C′
(2)在图中画出△A′B′C′的高C′D′
巩固 如下图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积。
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
⑴请画出平移后的△A′B′C′.并求△A′B′C′的面积.
专题五 三角形内角和
例1 问题1
现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系
是
研究(2):如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是
研究(3):如果折成图③的形状,猜想∠1、∠2′和∠A的数量关系,并说明理由.
问题2
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .
图① 图②
图③
图④
例2 如图①,在ΔABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,ΔAˊBˊCˊ的外角平分线相交于点Oˊ,∠Aˊ=40°,
求∠BˊOˊCˊ的度数;
(3)上面(1)、(2)两题中的∠BOC与∠BˊOˊCˊ有怎样的数量关系?若∠A=∠Aˊ=n°,∠BOC与∠BˊOˊCˊ是否还具有这样的关系?这个结论你是怎样得到的?
巩固 如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于P点.
⑴若∠ABC=40°,∠ACB=80°,求∠P的度数;
⑵若∠A=60°,求∠P的度数;
⑶那么∠A和∠P有什么样的数量关系? 请简述理由.
专题六 简单的阅读
例1、观察下列等式,并回答有关问题:
;
;
;
…
(1)若n为正整数,猜想 ;
(2)利用上题的结论比较与的大小.
例2、次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图所示,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:。游戏规定:所持算式的值相等的两个人是朋友。如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法。
专题七 从面积到乘法公式的应用
例 我们运用图(I)图中大正方形的面积可表示为,也可表示为
,即由此推导出一个重要的结论,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a, 较小的直角边长都为b,斜边长都为c).
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证:
(3)请你自己设计图形的组合,用其面积表达式验证:
(a+b)(a+2b)=a2+3ab+2b2.
巩固 探索平方差公式时设置了如下情境:边长为b的小正方形纸片放置在边长为a的大正方形纸片上(如图9-6),你能通过计算未盖住部分的面积得到公式(a+b) (a-b)=a2-b2吗?(不必证明)
(1)如果将小正方形的一边延长(如图①),是否也能推导公式?请完成证明.
(2)面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图②,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4×ab+(a-b)2,由此推导出重要的勾股定理:a2+b2=c2.图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.
(3)试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在下面的网格中,并标出字母a、b所表示的线段.
二、 巩固练习
1、计算
(1)()-2-23×0.125 +20120 +|-1| (2)(-a2b3c4 )(-xa2b)2
(3)(-m)2·(m2)2 ÷ m 3 (4)-2a2(12ab+b2 )-5ab (a2-ab )
2、因式分解
(1) x3+2x2y+xy2 (2)m2(m-1)+4(1-m)
3、如图,AB∥DC,∠ABC=∠ADC,问:AE与FC平行吗?请说明理由.
4、在△ABC中,AD是高,AE是角平分线.,∠B=20°,∠C=60,求∠CAD和∠DAE的
度数。
5、如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角. (提示: 有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
6、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC
和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
__________________________________________.
答案解析:
一、专题精讲
专题一 计算
例1 化简计算
1、 2、
3、 4、
答案:
1、解:原式=
=
=
2、解:原式=
=
3、解:原式=
=
=
4、解:原式=
=
=
例2 因式分解
1、 2、
3、 4、
答案:
1、解:原式=
=
2、解:原式=
=
3、解:原式=
=
4、解:原式=
=
=
专题二 计算的应用
例1 化简求值:(3x+2)(3x-2)-5x(3x-2)+(2-3x)2,其中x=-.
巩固 已知:(x+a)(x-)的结果中不含关于字母的一次项,求的值
例2、我们学习了因式分解之后可以解某些高次方程,例如,一元二次方程x2+x-2=0可以通过因式分解化为:(x-1)(x+2)=0,则方程的两个解为x=1和x=-2.反之,如果x=1是某方程ax2+bx+c=0的一个解,则多项式ax2+bx+c必有一个因式是 (x-1),在理解上文的基础上,试找出多项式x3+x2-3x+1的一个因式,并将这个多项式因式分解.
专题三 平行
例1 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
答案(1).理由如下:
∵ ,,
∴ .
∴ .
(2)∵ ,
∴ .
∵ ,
∴ .
∴ .
∴ .
巩固 小玲观察下图得出“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等”这个结论,你是否认同小玲的观点?如果认同,则给出证明;如果不认同,则画出所有可能的情况,猜想相应的结论,并给出证明.
答案:
例2、在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:
∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=∠ABC,(角的平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
答案:
专题三 平行中求面积
例1 (1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;
(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO的面积相等;
(3)如图3,点M在△ABC的边上, 过点M画一条平分三角形面积的直线.
解:(1)取BC的中点D,过A、D画直线,则直线AD为所求;
(2)∵l1∥l2,
∴点E,F到l2之间的距离都相等,设为h.
∴S△EGH=GH?h,S△FGH=GH?h,
∴S△EGH=S△FGH,
∴S△EGH-S△GOH=S△FGH-S△GOH,
∴△EGO的面积等于△FGO的面积;
(3) 取BC的中点D,连接MD,过点A作AN∥MD交BC 于点N,过M、N画直线,则直线MN为所求.
巩固、
探索:在图1至图3中,已知△ABC的面积为a,
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1= (用含a的代数式表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2= (用含a的代数式表示)
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3= (用含a的代数式表示)
并运用上述(2)的结论写出理由.发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 .
应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
①种紫花的区域的面积;
②种蓝花的区域的面积.
解:(1)a
(2)2a
(3)6a; 7倍
①黄花区域的面积是6×10=60平方米
紫花区域的面积是6×(60+10)=420平方米
②蓝花区域的面积是6 ×(420+60+10)=2940平方米
专题四 操作题
例 如图,每个小正方形边长为1,△ABC的顶点都在方格纸的格点上,将△ABC向下平移3格,再向右平移4格.
(1)请在图中画出平移后的△A′B′C′
(2)在图中画出△A′B′C′的高C′D′
答案:如图所示
巩固 如下图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积。
答案:S△ABC = 8
注意:讲解格点中求面积
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
⑴请画出平移后的△A′B′C′.并求△A′B′C′的面积.
专题五 三角形内角和
例1 问题1
现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系
是
研究(2):如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是
研究(3):如果折成图③的形状,猜想∠1、∠2′和∠A的数量关系,并说明理由.
问题2
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .
图① 图②
图③
图④
解:(1)根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,故∠BDA′=2∠A;
(2)由图形折叠的性质可知,∠CEA′=180°-2∠DEA′…①,∠BDA′=180°-2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°-2(180°-∠A),
故∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'-∠CEA'=2∠A,
(4)如图④,由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,
两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE)
即∠1+∠2=360°-2(360°-∠A-∠B),
所以,∠1+∠2=2(∠A+∠B)-360°.
例2 如图①,在ΔABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,ΔAˊBˊCˊ的外角平分线相交于点Oˊ,∠Aˊ=40°,
求∠BˊOˊCˊ的度数;
(3)上面(1)、(2)两题中的∠BOC与∠BˊOˊCˊ有怎样的数量关系?若∠A=∠Aˊ=n°,∠BOC与∠BˊOˊCˊ是否还具有这样的关系?这个结论你是怎样得到的?
答案:
1、∠ABC+∠ACB=180-40=140°
所以∠OBC+∠OCB=∠ABC+∠ACB=×140=70°
所以∠BOC=180-70=110°
2.∠ABC+∠ACB=180-40=140°
外角和内角互补
所以两个外角相加=180+180-140=220°
则∠O'BC+∠O'CB=220×=110°
3.∠BOC=∠B'O'C'
∠A=∠A'=n
则∠BOC=180-(180-n)×=90+n×
∠B'O'C'=180-[360-(180-n)]×=90-n×
所以不论n是多少
都有∠BOC与∠B'O'C'互补
巩固 如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于P点.
⑴若∠ABC=40°,∠ACB=80°,求∠P的度数;
⑵若∠A=60°,求∠P的度数;
⑶那么∠A和∠P有什么样的数量关系? 请简述理由.
答案:30°;30°;∠P=∠A
专题六 简单的阅读
例1、观察下列等式,并回答有关问题:
;
;
;
…
(1)若n为正整数,猜想 ;
(2)利用上题的结论比较与的大小.
答案:(1)
(2)=
=
=>
所以>
例2、次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图所示,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:。游戏规定:所持算式的值相等的两个人是朋友。如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法。
答案:
巩固 若一个正整数能表示为两个连续偶数的平方差,那么这个正整数为“神秘数”如4,12,20这三个数都是神秘数
(1)28和76是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(k为非负整数)由这两个连续偶数构成的神秘数是4的倍数吗?为什么?(4分)
解:(1)设28和2012都是“神秘数”,设28是x和x-2两数的平方差得到,
则x2-(x-2)2=28,
解得:x=8,∴x-2=6,
即28=82-62,
设2012是y和y-2两数的平方差得到,
则y2-(y-2)2=2012,
解得:y=504,
y-2=502,
即2012=5042-5022,
所以28,2012都是神秘数.
(2)(2k+2)2-(2k)2=(2k+2-2k)(2k+2+2k)=4(2k+1),
∴由2k+2和2k构造的神秘数是4的倍数.
(3)设两个连续奇数为2k+1和2k-1,
则(2k+1)2-(2k-1)2=8k=4×2k,
∴两个连续奇数的平方差不是神秘数.
专题七 从面积到乘法公式的应用
例 我们运用图(I)图中大正方形的面积可表示为,也可表示为
,即由此推导出一个重要的结论,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a, 较小的直角边长都为b,斜边长都为c).
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证:
(3)请你自己设计图形的组合,用其面积表达式验证:
(a+b)(a+2b)=a2+3ab+2b2.
解:(1)(a-b)2=c2-4(ab)
∴a2+b2=c2;
(2)如图:
;
(3)如图:
则(a+b)(a+2b)=a2+3ab+2b2。
巩固 探索平方差公式时设置了如下情境:边长为b的小正方形纸片放置在边长为a的大正方形纸片上(如图9-6),你能通过计算未盖住部分的面积得到公式(a+b) (a-b)=a2-b2吗?(不必证明)
(1)如果将小正方形的一边延长(如图①),是否也能推导公式?请完成证明.
(2)面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图②,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4×ab+(a-b)2,由此推导出重要的勾股定理:a2+b2=c2.图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.
(3)试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在下面的网格中,并标出字母a、b所表示的线段.
答案:
二、巩固练习
1、计算
(1)()-2-23×0.125 +20120 +|-1| (2)(-a2b3c4 )(-xa2b)2
(3)(-m)2·(m2)2 ÷ m 3 (4)-2a2(12ab+b2 )-5ab (a2-ab )
答案:
(1)()-2-23×0.125 +20120 +|-1| (2)(-a2b3c4 )(-xa2b)2
(3)(-m)2·(m2)2 ÷ m 3 (4)-2a2(12ab+b2)-5ab(a2-ab)
2、因式分解
(1) x3+2x2y+xy2 (2)m2(m-1)+4(1-m)
答案:
(1) x3+2x2y+xy2 (2) m2(m-1)+4(1-m)
3、如图,AB∥DC,∠ABC=∠ADC,问:AE与FC平行吗?请说明理由.
答案:平行
4、在△ABC中,AD是高,AE是角平分线.,∠B=20°,∠C=60,求∠CAD和∠DAE的
度数。
答案:∠CAD=30°(2分),∠DAE=20°
5、如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角. (提示: 有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
答案:(1)略 (2) 不成立∠APB+∠PAC+∠PBD=3600
(3)在 AB左侧: ∠APB=∠PAC-∠PBD
在 AB上: ∠APB=∠PAC-∠PBD (∠APB=∠PBD-∠PAC)
在 AB右侧: ∠APB=∠PBD-∠PAC
6、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC
和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
__________________________________________.
答案:
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
=4-1+1+1
=5
=-a2b3c4 ·x2a4b2
=-x2a6b5c4
=-24a3b-2a2b2-5a3b+5 a2b2
=-29a3b+3a2b2
=m2·m4÷m3
= m3
= (m-1) ( m2-4)
= (m-1) ( m+2) ( m-2)
= x(x2+2xy+y2)
= x(x+y) 2
学习目标:复习巩固数学前三章重要知识点题型
一、专题精讲
专题一 计算
例1 化简计算
1、 2、
3、 4、
例2 因式分解
1、 2、
3、 4、
专题二 计算的应用
例1 化简求值:(3x+2)(3x-2)-5x(3x-2)+(2-3x)2,其中x=-.
巩固 已知:(x+a)(x-)的结果中不含关于字母的一次项,求的值
例2、我们学习了因式分解之后可以解某些高次方程,例如,一元二次方程x2+x-2=0可以通过因式分解化为:(x-1)(x+2)=0,则方程的两个解为x=1和x=-2.反之,如果x=1是某方程ax2+bx+c=0的一个解,则多项式ax2+bx+c必有一个因式是 (x-1),在理解上文的基础上,试找出多项式x3+x2-3x+1的一个因式,并将这个多项式因式分解.
专题三 平行
例1 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
巩固 小玲观察下图得出“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等”这个结论,你是否认同小玲的观点?如果认同,则给出证明;如果不认同,则画出所有可能的情况,猜想相应的结论,并给出证明.
例2、在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:
∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=∠ABC,(角的平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
专题三 平行中求面积
例1 (1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;
(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO的面积相等;
(3)如图3,点M在△ABC的边上, 过点M画一条平分三角形面积的直线.
巩固、
探索:在图1至图3中,已知△ABC的面积为a,
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1= (用含a的代数式表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2= (用含a的代数式表示)
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3= (用含a的代数式表示)
并运用上述(2)的结论写出理由.发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 .
应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
①种紫花的区域的面积;
②种蓝花的区域的面积.
专题四 操作题
例 如图,每个小正方形边长为1,△ABC的顶点都在方格纸的格点上,将△ABC向下平移3格,再向右平移4格.
(1)请在图中画出平移后的△A′B′C′
(2)在图中画出△A′B′C′的高C′D′
巩固 如下图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积。
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
⑴请画出平移后的△A′B′C′.并求△A′B′C′的面积.
专题五 三角形内角和
例1 问题1
现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系
是
研究(2):如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是
研究(3):如果折成图③的形状,猜想∠1、∠2′和∠A的数量关系,并说明理由.
问题2
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .
图① 图②
图③
图④
例2 如图①,在ΔABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,ΔAˊBˊCˊ的外角平分线相交于点Oˊ,∠Aˊ=40°,
求∠BˊOˊCˊ的度数;
(3)上面(1)、(2)两题中的∠BOC与∠BˊOˊCˊ有怎样的数量关系?若∠A=∠Aˊ=n°,∠BOC与∠BˊOˊCˊ是否还具有这样的关系?这个结论你是怎样得到的?
巩固 如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于P点.
⑴若∠ABC=40°,∠ACB=80°,求∠P的度数;
⑵若∠A=60°,求∠P的度数;
⑶那么∠A和∠P有什么样的数量关系? 请简述理由.
专题六 简单的阅读
例1、观察下列等式,并回答有关问题:
;
;
;
…
(1)若n为正整数,猜想 ;
(2)利用上题的结论比较与的大小.
例2、次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图所示,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:。游戏规定:所持算式的值相等的两个人是朋友。如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法。
专题七 从面积到乘法公式的应用
例 我们运用图(I)图中大正方形的面积可表示为,也可表示为
,即由此推导出一个重要的结论,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a, 较小的直角边长都为b,斜边长都为c).
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证:
(3)请你自己设计图形的组合,用其面积表达式验证:
(a+b)(a+2b)=a2+3ab+2b2.
巩固 探索平方差公式时设置了如下情境:边长为b的小正方形纸片放置在边长为a的大正方形纸片上(如图9-6),你能通过计算未盖住部分的面积得到公式(a+b) (a-b)=a2-b2吗?(不必证明)
(1)如果将小正方形的一边延长(如图①),是否也能推导公式?请完成证明.
(2)面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图②,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4×ab+(a-b)2,由此推导出重要的勾股定理:a2+b2=c2.图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.
(3)试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在下面的网格中,并标出字母a、b所表示的线段.
二、 巩固练习
1、计算
(1)()-2-23×0.125 +20120 +|-1| (2)(-a2b3c4 )(-xa2b)2
(3)(-m)2·(m2)2 ÷ m 3 (4)-2a2(12ab+b2 )-5ab (a2-ab )
2、因式分解
(1) x3+2x2y+xy2 (2)m2(m-1)+4(1-m)
3、如图,AB∥DC,∠ABC=∠ADC,问:AE与FC平行吗?请说明理由.
4、在△ABC中,AD是高,AE是角平分线.,∠B=20°,∠C=60,求∠CAD和∠DAE的
度数。
5、如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角. (提示: 有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
6、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC
和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
__________________________________________.
答案解析:
一、专题精讲
专题一 计算
例1 化简计算
1、 2、
3、 4、
答案:
1、解:原式=
=
=
2、解:原式=
=
3、解:原式=
=
=
4、解:原式=
=
=
例2 因式分解
1、 2、
3、 4、
答案:
1、解:原式=
=
2、解:原式=
=
3、解:原式=
=
4、解:原式=
=
=
专题二 计算的应用
例1 化简求值:(3x+2)(3x-2)-5x(3x-2)+(2-3x)2,其中x=-.
巩固 已知:(x+a)(x-)的结果中不含关于字母的一次项,求的值
例2、我们学习了因式分解之后可以解某些高次方程,例如,一元二次方程x2+x-2=0可以通过因式分解化为:(x-1)(x+2)=0,则方程的两个解为x=1和x=-2.反之,如果x=1是某方程ax2+bx+c=0的一个解,则多项式ax2+bx+c必有一个因式是 (x-1),在理解上文的基础上,试找出多项式x3+x2-3x+1的一个因式,并将这个多项式因式分解.
专题三 平行
例1 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
答案(1).理由如下:
∵ ,,
∴ .
∴ .
(2)∵ ,
∴ .
∵ ,
∴ .
∴ .
∴ .
巩固 小玲观察下图得出“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等”这个结论,你是否认同小玲的观点?如果认同,则给出证明;如果不认同,则画出所有可能的情况,猜想相应的结论,并给出证明.
答案:
例2、在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:
∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=∠ABC,(角的平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
答案:
专题三 平行中求面积
例1 (1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;
(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO的面积相等;
(3)如图3,点M在△ABC的边上, 过点M画一条平分三角形面积的直线.
解:(1)取BC的中点D,过A、D画直线,则直线AD为所求;
(2)∵l1∥l2,
∴点E,F到l2之间的距离都相等,设为h.
∴S△EGH=GH?h,S△FGH=GH?h,
∴S△EGH=S△FGH,
∴S△EGH-S△GOH=S△FGH-S△GOH,
∴△EGO的面积等于△FGO的面积;
(3) 取BC的中点D,连接MD,过点A作AN∥MD交BC 于点N,过M、N画直线,则直线MN为所求.
巩固、
探索:在图1至图3中,已知△ABC的面积为a,
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1= (用含a的代数式表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2= (用含a的代数式表示)
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3= (用含a的代数式表示)
并运用上述(2)的结论写出理由.发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 .
应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
①种紫花的区域的面积;
②种蓝花的区域的面积.
解:(1)a
(2)2a
(3)6a; 7倍
①黄花区域的面积是6×10=60平方米
紫花区域的面积是6×(60+10)=420平方米
②蓝花区域的面积是6 ×(420+60+10)=2940平方米
专题四 操作题
例 如图,每个小正方形边长为1,△ABC的顶点都在方格纸的格点上,将△ABC向下平移3格,再向右平移4格.
(1)请在图中画出平移后的△A′B′C′
(2)在图中画出△A′B′C′的高C′D′
答案:如图所示
巩固 如下图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积。
答案:S△ABC = 8
注意:讲解格点中求面积
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
⑴请画出平移后的△A′B′C′.并求△A′B′C′的面积.
专题五 三角形内角和
例1 问题1
现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系
是
研究(2):如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是
研究(3):如果折成图③的形状,猜想∠1、∠2′和∠A的数量关系,并说明理由.
问题2
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .
图① 图②
图③
图④
解:(1)根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,故∠BDA′=2∠A;
(2)由图形折叠的性质可知,∠CEA′=180°-2∠DEA′…①,∠BDA′=180°-2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°-2(180°-∠A),
故∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'-∠CEA'=2∠A,
(4)如图④,由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,
两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE)
即∠1+∠2=360°-2(360°-∠A-∠B),
所以,∠1+∠2=2(∠A+∠B)-360°.
例2 如图①,在ΔABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,ΔAˊBˊCˊ的外角平分线相交于点Oˊ,∠Aˊ=40°,
求∠BˊOˊCˊ的度数;
(3)上面(1)、(2)两题中的∠BOC与∠BˊOˊCˊ有怎样的数量关系?若∠A=∠Aˊ=n°,∠BOC与∠BˊOˊCˊ是否还具有这样的关系?这个结论你是怎样得到的?
答案:
1、∠ABC+∠ACB=180-40=140°
所以∠OBC+∠OCB=∠ABC+∠ACB=×140=70°
所以∠BOC=180-70=110°
2.∠ABC+∠ACB=180-40=140°
外角和内角互补
所以两个外角相加=180+180-140=220°
则∠O'BC+∠O'CB=220×=110°
3.∠BOC=∠B'O'C'
∠A=∠A'=n
则∠BOC=180-(180-n)×=90+n×
∠B'O'C'=180-[360-(180-n)]×=90-n×
所以不论n是多少
都有∠BOC与∠B'O'C'互补
巩固 如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于P点.
⑴若∠ABC=40°,∠ACB=80°,求∠P的度数;
⑵若∠A=60°,求∠P的度数;
⑶那么∠A和∠P有什么样的数量关系? 请简述理由.
答案:30°;30°;∠P=∠A
专题六 简单的阅读
例1、观察下列等式,并回答有关问题:
;
;
;
…
(1)若n为正整数,猜想 ;
(2)利用上题的结论比较与的大小.
答案:(1)
(2)=
=
=>
所以>
例2、次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图所示,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:。游戏规定:所持算式的值相等的两个人是朋友。如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法。
答案:
巩固 若一个正整数能表示为两个连续偶数的平方差,那么这个正整数为“神秘数”如4,12,20这三个数都是神秘数
(1)28和76是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(k为非负整数)由这两个连续偶数构成的神秘数是4的倍数吗?为什么?(4分)
解:(1)设28和2012都是“神秘数”,设28是x和x-2两数的平方差得到,
则x2-(x-2)2=28,
解得:x=8,∴x-2=6,
即28=82-62,
设2012是y和y-2两数的平方差得到,
则y2-(y-2)2=2012,
解得:y=504,
y-2=502,
即2012=5042-5022,
所以28,2012都是神秘数.
(2)(2k+2)2-(2k)2=(2k+2-2k)(2k+2+2k)=4(2k+1),
∴由2k+2和2k构造的神秘数是4的倍数.
(3)设两个连续奇数为2k+1和2k-1,
则(2k+1)2-(2k-1)2=8k=4×2k,
∴两个连续奇数的平方差不是神秘数.
专题七 从面积到乘法公式的应用
例 我们运用图(I)图中大正方形的面积可表示为,也可表示为
,即由此推导出一个重要的结论,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a, 较小的直角边长都为b,斜边长都为c).
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证:
(3)请你自己设计图形的组合,用其面积表达式验证:
(a+b)(a+2b)=a2+3ab+2b2.
解:(1)(a-b)2=c2-4(ab)
∴a2+b2=c2;
(2)如图:
;
(3)如图:
则(a+b)(a+2b)=a2+3ab+2b2。
巩固 探索平方差公式时设置了如下情境:边长为b的小正方形纸片放置在边长为a的大正方形纸片上(如图9-6),你能通过计算未盖住部分的面积得到公式(a+b) (a-b)=a2-b2吗?(不必证明)
(1)如果将小正方形的一边延长(如图①),是否也能推导公式?请完成证明.
(2)面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图②,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4×ab+(a-b)2,由此推导出重要的勾股定理:a2+b2=c2.图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.
(3)试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在下面的网格中,并标出字母a、b所表示的线段.
答案:
二、巩固练习
1、计算
(1)()-2-23×0.125 +20120 +|-1| (2)(-a2b3c4 )(-xa2b)2
(3)(-m)2·(m2)2 ÷ m 3 (4)-2a2(12ab+b2 )-5ab (a2-ab )
答案:
(1)()-2-23×0.125 +20120 +|-1| (2)(-a2b3c4 )(-xa2b)2
(3)(-m)2·(m2)2 ÷ m 3 (4)-2a2(12ab+b2)-5ab(a2-ab)
2、因式分解
(1) x3+2x2y+xy2 (2)m2(m-1)+4(1-m)
答案:
(1) x3+2x2y+xy2 (2) m2(m-1)+4(1-m)
3、如图,AB∥DC,∠ABC=∠ADC,问:AE与FC平行吗?请说明理由.
答案:平行
4、在△ABC中,AD是高,AE是角平分线.,∠B=20°,∠C=60,求∠CAD和∠DAE的
度数。
答案:∠CAD=30°(2分),∠DAE=20°
5、如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角. (提示: 有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
答案:(1)略 (2) 不成立∠APB+∠PAC+∠PBD=3600
(3)在 AB左侧: ∠APB=∠PAC-∠PBD
在 AB上: ∠APB=∠PAC-∠PBD (∠APB=∠PBD-∠PAC)
在 AB右侧: ∠APB=∠PBD-∠PAC
6、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC
和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
__________________________________________.
答案:
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
=4-1+1+1
=5
=-a2b3c4 ·x2a4b2
=-x2a6b5c4
=-24a3b-2a2b2-5a3b+5 a2b2
=-29a3b+3a2b2
=m2·m4÷m3
= m3
= (m-1) ( m2-4)
= (m-1) ( m+2) ( m-2)
= x(x2+2xy+y2)
= x(x+y) 2
同课章节目录
