北京数学五上密铺教案
图片预览




文档简介
6密铺
1 教学目标
1.过观察生活中常见的密铺现象,使学生初步理解密铺的含义,知道什么是平面图形的密铺;通过摆一摆、拼一拼等实践活动,探索三角形、平行四边形、梯形、正五边形、正六边形、正八边形、圆是否可以密铺,认识一些可以密铺的平面图形,在操作的过程中感受能够密铺的平面图形的特点。
2.在探究图形密铺的过程中,使学生经历观察、猜测、推理、验证和交流等过程,并尝试用一种或两种平面图形进行密铺设计,培养学生的空间观念,进一步发展学生的动手实践能力、合情推理能力和创新能力。
3.使学生在欣赏密铺图案和设计简单的密铺图案的过程中,体会图形的转换,感受数学知识与生活的密切联系,经历欣赏数学美、创造数学美的过程,从而激发学生学习数学的兴趣,体验学习数学的价值。同时,进一步发展学生的团结合作意识,享受由合作获得成功的喜悦。
2学情分析
五年级学生虽然已经进入了第二学段的学习,他们已经具备一定的知识经验,但是还是有较强的好奇心,也有较强的表现欲;他们的思维以直接经验为主,间接经验仍然相对较少;对于密铺,学生已经有了较为直观的生活体验,只是还未形成系统的理论知识。从知识准备上,五年级学生已经学习了图形的平移、旋转,认识了长方形、正方形、平行四边形、梯形、三角形等图形的特征,及三角形的内角和是180?等知识,并积累了图形拼摆操作的学习经验。从能力和方法水平上,五年级学生已经具备一定的推理能力,能初步运用“猜想——验证——归纳”的数学思想方法来探究问题。
3重点难点
教学重点:通过观察、操作、思考和简单设计等活动,掌握密铺的特点,知道哪些图形可单独进行密铺。
教学难点:理解密铺的特点,体会密铺的条件,能进行简单的密铺设计。
4教学过程
4.1 第一学时
4.1.1教学活动
活动1【导入】精彩3分钟:拼图游戏+拼图历史介绍(3’)
1.同学们:大家好!今天我给大家带来一个拼图小游戏。伸手指表示出你的选择。正确!将图1直接拼过去肯定不行,但是旋转一下再拼就可以了。而图2太小了,不能铺满。
2.再来看一个,寻找失踪的第15块拼图。出手指。选2的同学对了,选1有空隙,选3有重叠。
3.同学们你们会玩拼图,那你们知道拼图的历史吗?下面就由我给大家介绍一下拼图的历史。
拼图玩具距今已有235年的历史了。
早在1760年,法国和英国两国几乎同时出现拼图游戏。人们把一张图片粘在硬纸板上,然后把它剪成不规则的小碎片。
1762年,推销商迪马开始推销地图拼图。这种地图拼图要求把碎片重新排列,是一种很文雅的娱乐活动。同年在伦敦,印刷工约翰·斯皮尔斯伯,发明了经久不衰的拼图玩具。他极其巧妙地把一幅英国地图,粘到一张很薄的餐桌背面,然后沿着各郡县的边缘精确地把地图切割成小块。
1789年,约翰-沃利斯发明了色彩明亮的风景画拼图,现代拼图诞生了。
1840年左右,德国和法国的拼图制造商用软木材、夹板和纸板代替硬木薄板,大大降低了成本。人们可以用低廉的价格买到自己喜欢的拼图,无论是大人还是孩子都沉浸在拼图游戏的快乐之中。
活动2【导入】一、创设情境,感知密铺(5’)
1.生活引入
感谢**给我们带来拼图中的智慧!拼图是一种益智玩具,每块儿拼图都要紧凑地拼插在一起,不留空隙,不重叠。
建筑工人们工作时,有时也像在玩“拼图”,想不想看一看?下面我们一起欣赏建筑工人的智慧。(课件出示:广场、街道、房间地面、墙壁等场景图片。)
??????
2.建立概念
(1)为什么说建筑工人好像在玩“拼图”呢?
预设:因为他们在铺地或是铺墙的时候,也像玩拼图一样,一块儿挨着一块儿地铺,中间不留空隙,也不重叠。
【设计意图】呈现铺地砖、瓷砖的图片,激发学生学习数学的兴趣,让学生在游戏和熟悉的生活场景中,感受到密铺现象在生活中的存在。
(2)密铺的科学定义
仔细看,这些地砖或墙砖它们一块儿挨一块儿,不留空隙,也不重叠。
像这样,用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
无空隙、不重叠是密铺的两大本质特征。(板书:无空隙? 不重叠)
(3)揭示课题
今天我们就一起来研究平面图形的密铺。(板书课题:密铺)
3.巩固概念
仔细观察下面的这几幅图,可以看作是密铺吗?你是怎么想的?
(1)圆形的密铺
评:同学们紧紧抓住密铺“无空隙”、“不重叠”的铺满平面的特点进行判断,特别好。这样看来圆形不能单独密铺。(贴图圆形,板书:不能)
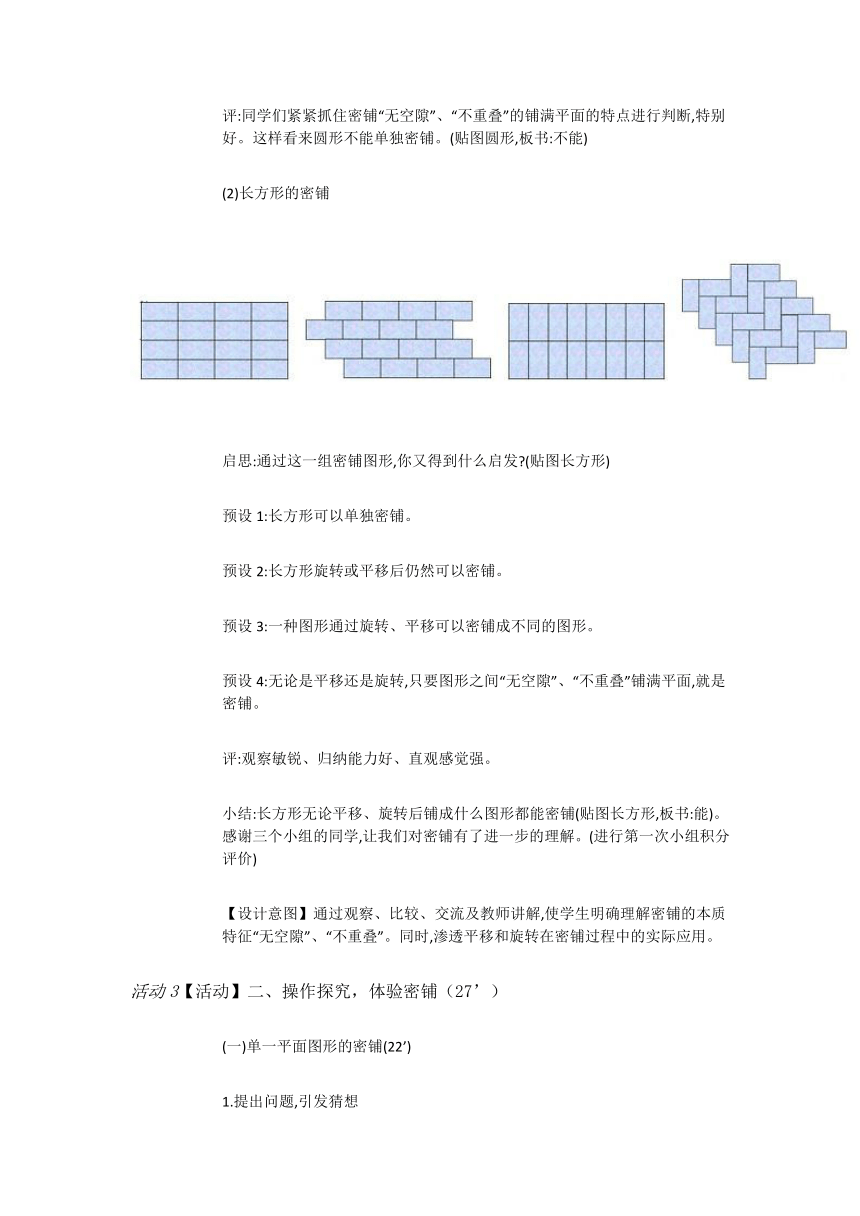
(2)长方形的密铺
启思:通过这一组密铺图形,你又得到什么启发?(贴图长方形)
预设1:长方形可以单独密铺。
预设2:长方形旋转或平移后仍然可以密铺。
预设3:一种图形通过旋转、平移可以密铺成不同的图形。
预设4:无论是平移还是旋转,只要图形之间“无空隙”、“不重叠”铺满平面,就是密铺。
评:观察敏锐、归纳能力好、直观感觉强。
小结:长方形无论平移、旋转后铺成什么图形都能密铺(贴图长方形,板书:能)。感谢三个小组的同学,让我们对密铺有了进一步的理解。(进行第一次小组积分评价)
【设计意图】通过观察、比较、交流及教师讲解,使学生明确理解密铺的本质特征“无空隙”、“不重叠”。同时,渗透平移和旋转在密铺过程中的实际应用。
活动3【活动】二、操作探究,体验密铺(27’)
(一)单一平面图形的密铺(22’)
1.提出问题,引发猜想
通过刚才的学习,我们发现长方形可以单独密铺,圆形不可以单独密铺。其实,无论多么复杂的图案都是由一些简单的基本图形构成的,下面我们就从简单的平面图形开始研究。
??
(1)(多媒体课件出示)这些平面图形,你认识他们吗?
(2)仔细观察,根据你的经验和感觉,哪种图形可以单独密铺呢?
评:很多研究都是从大胆猜测开始的。
(3)用什么方法验证大家的猜测呢?(动手铺一铺)
评:这个办法好,实践出真知!
2.小组合作,实践验证
请看操作要求:(课件出示活动要求)
(1)每人选择一种图形铺一铺(因只有图形种类有限,组长先进行协调,适当安排部分同学两人合作)。
(2)把铺得的作品在小组展示,并交流验证的结果。
师:揭开操作盒1,限时2分钟,开始。(教师操作计时器)
3.展示成果,汇报交流
(1)小组展示:哪个小组愿意到前边来展示,告诉大家你验证了哪种图形,它能不能单独密铺。
评:操作认真、态度严谨、用概念判断、合作高效、表达清晰。
(2)全班互动:
他们得到的结论,你们同意吗?
①哪些图形能单独密铺?(教师贴图:等边三角形、正方形、正六边形)
把你们用等边三角形、正方形和正六边形密铺的作品面向大家,举起来,大家互相看一看。
虽然大家密铺成的图形不同,但结论是一样的,等边三角形、正方形和正六边形可以单独密铺。
②哪些图形不能单独密铺?(教师贴图:正五边形、正八边形)
举起你们的作品让全班同学欣赏欣赏。
正五边形和正八边形无论怎样拼摆,总有空隙,所以正五边形和正八边形和圆一样,都不能单独密铺。
(3)小结:刚才我们先观察猜测,然后操作验证,最后归纳概括。发现等边三角形、正方形和正六边形可以单独密铺,正五边形和正八边形不能单独密铺。(板书:观察猜测——操作验证——归纳概括)合作效率真高!(进行第二次小组积分评价)
【设计意图】让学生经历观察猜测、操作验证、归纳概括的过程,判断常见的正多边形哪些能密铺,哪些不能密铺,在合作中进行密铺操作,进一步体会平面图形密铺的特点。
4.启疑激思,追寻本质
(1)鼓励质疑:这些图形有的能单独密铺,有的不能单独密铺,你有什么疑问吗?
预设1:为什么有的图形能单独密铺,有的图形不能单独密铺?
预设2:有的图形边相等,却也不能单独密铺?
预设3:我猜测一种图形能不能单独密铺,可能和图形的角度有关。
(2)媒体演示
①正三角形每个内角是60°,三个内角旋转拼在一起围绕中心点形成180°,六个拼在一起成360°。
②正方形每个内角是90°,两个拼在一起就是180°,四个拼在一起成360°。
③正六边形每个内角是120°,两个内角拼在一起大于180°了,三个拼在一起正好是360°。
④正五边形每个内角是108°,两个内角拼在一起大于180°了,三个拼在一起接近360°,但仍然有空隙,如果再拼一个就重叠了,所以不能密铺。
⑤正八边形每个内角是135°,两个内角拼在一起270°,三个内角拼在一起有重叠了,所以不能密铺。
小结:通过观察,你觉得一个图形能否单独密铺和什么有关系?(一个拼接点处的所有角的和为360°。)
【设计意图】通过启发学生质疑,鼓励学生深入思考问题,通过多媒体动态演示,帮助学生初步建立正多边形密铺的基本条件,一个拼接点处的所有角的和为360°。
5.联系生活,拓展延伸
(1)其实我们生活中,很多精美的图案都是密铺得来的,想一想生活中还有哪些密铺的现象?
(2)图形的密铺在生活中应用广泛,人们也在用密铺完成着更奇妙的创造。(课件出示:棋盘、蜂巢、墙和门、水立方等图片)
? ?? ???
仔细观察水立方每个面上的图形,你有什么发现?
预设1:图形是不规则的。
预设2:不规则的平面图形也能密铺。
6.二次合作,深度密铺
(1)启发猜测? 布置任务
下面这些图形都不是正多边形,它们能单独密铺吗?
???
课件出示小组活动要求:
①观察猜测:把观察猜测记录在《学习报告单》上。
②验证交流:每人选择一种图形进行验证,并在组内进行交流。
③记录结果:把操作验证的结果记录在《学习报告单》上。
④想一想:你们有什么新发现?
(2)小组合作? 实践探究
师:将上一次操作的图形放回操作盒1,打开操作盒2,限时3分钟,开始。(教师操作计时器)
(3)成果展示? 汇报交流
师:请一个小组来展示,并回应全班:这些三角形和四边形都能单独密铺。举起每个人的密铺作品大家看一看。
(4)设疑激思? 引发思考
评:同学合作高效、概括能力强、动手能力强。各个小组真是太智慧了,发现任意的三角形和四边形都能单独密铺。(进行第三次小组积分评价。)这是为什么呢?
预设1:两个完全一样的三角形能拼摆成一个平行四边形(或长方形),平行四边形(或长方形)能密铺,所以任意三角形都能密铺。
预设2:两个完全一样的梯形能拼摆成一个平行四边形,平行四边形能密铺,所以任意三角形都能密铺。
预设3:四边形的内角和是360?,围绕拼接点能拼成360?,所以任意四边形都能单独密铺。
预设4:三角形内角和是180?,围绕拼接点总能拼成360?,所以任意三角形都能单独密铺。
配合学生发言,教师随机展示交互式课件。
评:把新图形转化成已知图形、推理能力、善学习善思考。
【设计意图】一般三角形和四边形能否密铺,对于学生来说不容易进行想像,再次为学生提供拼摆操作的机会,学生通过动手操作和联系旧知,为密铺的研究进行了拓展与延伸,加深了对图形特征的认识,同时沟通了新旧知识之间的联系,发展了学生的逻辑思维能力。
6.冥想总结,加深理解
闭上眼睛,我们一起回顾一下刚才的研究过程,我们通过观察猜测、操作验证、最后得出结论,发现长方形、正方形、任意的三角形、任意的四边形、正六边形都能单独密铺,正五边形、正八边形和圆不能单独密铺。
【设计意图】在探讨单一平面图形的密铺过程中,教师从正多边形拓展到普通三角形和四边形的密铺,紧密联系图形的特征,结合图形的平移、旋转等变换方法,激发学生努力发挥想象力,在猜测、验证、讨论中加深对密铺条件的理解,发展了学生的推理、归纳、概括能力。
(二)两种平面图形的密铺(5’)
1.观察想像,诱发创新
正五边形、正八边形和圆不能单独密铺,但如果与其他图形结合起来,能不能实现密铺呢?
如果用圆、正五边形、正八边形与另外一种平面图形组合进行密铺,你会分别选择下面哪个图形与他们搭配?
???????
【设计意图】引导学生观察、想像,选择两种平面图形搭配进行密铺,有效地培养学生的空间想像力。
活动4【讲授】三、欣赏作品,渗透文化(2’)
提到密铺,不得不向大家介绍一个人——荷兰著名画家埃舍尔。他的作品令人赏心悦目,趣味无穷。人们称埃舍尔是“图形的艺术家”,是数学与艺术完美结合的典范。
? ?? ?? ??
【设计意图】通过初步了解密铺的历史,欣赏埃舍尔的优秀作品,感受数学与艺术的完美结合,图形密铺的神奇和美妙,同时使学生感受到艺术家的伟大创造力,为学生梳理刻苦钻研的意识,促进学生用数学的眼光观察生活、发现生活、分析生活、解决生活问题的意识和习惯。
活动5【作业】四、布置作业,拓展延伸(1’)
很美吧?你们想不想也来设计一幅作品呢?(课件出示:动手试一试和小小设计师要求)
1.动手试一试:用画一画或摆一摆的方法,继续探索下面的图形能不能单独密铺。
????????????
2.小小设计师:发挥你的想象,用至少两种不同的图形进行密铺,在方格纸上设计出美丽的图案,并涂上颜色。或者用彩色卡纸剪出两种及以上的不同图形,粘贴成一幅美丽的密铺作品。
1 教学目标
1.过观察生活中常见的密铺现象,使学生初步理解密铺的含义,知道什么是平面图形的密铺;通过摆一摆、拼一拼等实践活动,探索三角形、平行四边形、梯形、正五边形、正六边形、正八边形、圆是否可以密铺,认识一些可以密铺的平面图形,在操作的过程中感受能够密铺的平面图形的特点。
2.在探究图形密铺的过程中,使学生经历观察、猜测、推理、验证和交流等过程,并尝试用一种或两种平面图形进行密铺设计,培养学生的空间观念,进一步发展学生的动手实践能力、合情推理能力和创新能力。
3.使学生在欣赏密铺图案和设计简单的密铺图案的过程中,体会图形的转换,感受数学知识与生活的密切联系,经历欣赏数学美、创造数学美的过程,从而激发学生学习数学的兴趣,体验学习数学的价值。同时,进一步发展学生的团结合作意识,享受由合作获得成功的喜悦。
2学情分析
五年级学生虽然已经进入了第二学段的学习,他们已经具备一定的知识经验,但是还是有较强的好奇心,也有较强的表现欲;他们的思维以直接经验为主,间接经验仍然相对较少;对于密铺,学生已经有了较为直观的生活体验,只是还未形成系统的理论知识。从知识准备上,五年级学生已经学习了图形的平移、旋转,认识了长方形、正方形、平行四边形、梯形、三角形等图形的特征,及三角形的内角和是180?等知识,并积累了图形拼摆操作的学习经验。从能力和方法水平上,五年级学生已经具备一定的推理能力,能初步运用“猜想——验证——归纳”的数学思想方法来探究问题。
3重点难点
教学重点:通过观察、操作、思考和简单设计等活动,掌握密铺的特点,知道哪些图形可单独进行密铺。
教学难点:理解密铺的特点,体会密铺的条件,能进行简单的密铺设计。
4教学过程
4.1 第一学时
4.1.1教学活动
活动1【导入】精彩3分钟:拼图游戏+拼图历史介绍(3’)
1.同学们:大家好!今天我给大家带来一个拼图小游戏。伸手指表示出你的选择。正确!将图1直接拼过去肯定不行,但是旋转一下再拼就可以了。而图2太小了,不能铺满。
2.再来看一个,寻找失踪的第15块拼图。出手指。选2的同学对了,选1有空隙,选3有重叠。
3.同学们你们会玩拼图,那你们知道拼图的历史吗?下面就由我给大家介绍一下拼图的历史。
拼图玩具距今已有235年的历史了。
早在1760年,法国和英国两国几乎同时出现拼图游戏。人们把一张图片粘在硬纸板上,然后把它剪成不规则的小碎片。
1762年,推销商迪马开始推销地图拼图。这种地图拼图要求把碎片重新排列,是一种很文雅的娱乐活动。同年在伦敦,印刷工约翰·斯皮尔斯伯,发明了经久不衰的拼图玩具。他极其巧妙地把一幅英国地图,粘到一张很薄的餐桌背面,然后沿着各郡县的边缘精确地把地图切割成小块。
1789年,约翰-沃利斯发明了色彩明亮的风景画拼图,现代拼图诞生了。
1840年左右,德国和法国的拼图制造商用软木材、夹板和纸板代替硬木薄板,大大降低了成本。人们可以用低廉的价格买到自己喜欢的拼图,无论是大人还是孩子都沉浸在拼图游戏的快乐之中。
活动2【导入】一、创设情境,感知密铺(5’)
1.生活引入
感谢**给我们带来拼图中的智慧!拼图是一种益智玩具,每块儿拼图都要紧凑地拼插在一起,不留空隙,不重叠。
建筑工人们工作时,有时也像在玩“拼图”,想不想看一看?下面我们一起欣赏建筑工人的智慧。(课件出示:广场、街道、房间地面、墙壁等场景图片。)
??????
2.建立概念
(1)为什么说建筑工人好像在玩“拼图”呢?
预设:因为他们在铺地或是铺墙的时候,也像玩拼图一样,一块儿挨着一块儿地铺,中间不留空隙,也不重叠。
【设计意图】呈现铺地砖、瓷砖的图片,激发学生学习数学的兴趣,让学生在游戏和熟悉的生活场景中,感受到密铺现象在生活中的存在。
(2)密铺的科学定义
仔细看,这些地砖或墙砖它们一块儿挨一块儿,不留空隙,也不重叠。
像这样,用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
无空隙、不重叠是密铺的两大本质特征。(板书:无空隙? 不重叠)
(3)揭示课题
今天我们就一起来研究平面图形的密铺。(板书课题:密铺)
3.巩固概念
仔细观察下面的这几幅图,可以看作是密铺吗?你是怎么想的?
(1)圆形的密铺
评:同学们紧紧抓住密铺“无空隙”、“不重叠”的铺满平面的特点进行判断,特别好。这样看来圆形不能单独密铺。(贴图圆形,板书:不能)
(2)长方形的密铺
启思:通过这一组密铺图形,你又得到什么启发?(贴图长方形)
预设1:长方形可以单独密铺。
预设2:长方形旋转或平移后仍然可以密铺。
预设3:一种图形通过旋转、平移可以密铺成不同的图形。
预设4:无论是平移还是旋转,只要图形之间“无空隙”、“不重叠”铺满平面,就是密铺。
评:观察敏锐、归纳能力好、直观感觉强。
小结:长方形无论平移、旋转后铺成什么图形都能密铺(贴图长方形,板书:能)。感谢三个小组的同学,让我们对密铺有了进一步的理解。(进行第一次小组积分评价)
【设计意图】通过观察、比较、交流及教师讲解,使学生明确理解密铺的本质特征“无空隙”、“不重叠”。同时,渗透平移和旋转在密铺过程中的实际应用。
活动3【活动】二、操作探究,体验密铺(27’)
(一)单一平面图形的密铺(22’)
1.提出问题,引发猜想
通过刚才的学习,我们发现长方形可以单独密铺,圆形不可以单独密铺。其实,无论多么复杂的图案都是由一些简单的基本图形构成的,下面我们就从简单的平面图形开始研究。
??
(1)(多媒体课件出示)这些平面图形,你认识他们吗?
(2)仔细观察,根据你的经验和感觉,哪种图形可以单独密铺呢?
评:很多研究都是从大胆猜测开始的。
(3)用什么方法验证大家的猜测呢?(动手铺一铺)
评:这个办法好,实践出真知!
2.小组合作,实践验证
请看操作要求:(课件出示活动要求)
(1)每人选择一种图形铺一铺(因只有图形种类有限,组长先进行协调,适当安排部分同学两人合作)。
(2)把铺得的作品在小组展示,并交流验证的结果。
师:揭开操作盒1,限时2分钟,开始。(教师操作计时器)
3.展示成果,汇报交流
(1)小组展示:哪个小组愿意到前边来展示,告诉大家你验证了哪种图形,它能不能单独密铺。
评:操作认真、态度严谨、用概念判断、合作高效、表达清晰。
(2)全班互动:
他们得到的结论,你们同意吗?
①哪些图形能单独密铺?(教师贴图:等边三角形、正方形、正六边形)
把你们用等边三角形、正方形和正六边形密铺的作品面向大家,举起来,大家互相看一看。
虽然大家密铺成的图形不同,但结论是一样的,等边三角形、正方形和正六边形可以单独密铺。
②哪些图形不能单独密铺?(教师贴图:正五边形、正八边形)
举起你们的作品让全班同学欣赏欣赏。
正五边形和正八边形无论怎样拼摆,总有空隙,所以正五边形和正八边形和圆一样,都不能单独密铺。
(3)小结:刚才我们先观察猜测,然后操作验证,最后归纳概括。发现等边三角形、正方形和正六边形可以单独密铺,正五边形和正八边形不能单独密铺。(板书:观察猜测——操作验证——归纳概括)合作效率真高!(进行第二次小组积分评价)
【设计意图】让学生经历观察猜测、操作验证、归纳概括的过程,判断常见的正多边形哪些能密铺,哪些不能密铺,在合作中进行密铺操作,进一步体会平面图形密铺的特点。
4.启疑激思,追寻本质
(1)鼓励质疑:这些图形有的能单独密铺,有的不能单独密铺,你有什么疑问吗?
预设1:为什么有的图形能单独密铺,有的图形不能单独密铺?
预设2:有的图形边相等,却也不能单独密铺?
预设3:我猜测一种图形能不能单独密铺,可能和图形的角度有关。
(2)媒体演示
①正三角形每个内角是60°,三个内角旋转拼在一起围绕中心点形成180°,六个拼在一起成360°。
②正方形每个内角是90°,两个拼在一起就是180°,四个拼在一起成360°。
③正六边形每个内角是120°,两个内角拼在一起大于180°了,三个拼在一起正好是360°。
④正五边形每个内角是108°,两个内角拼在一起大于180°了,三个拼在一起接近360°,但仍然有空隙,如果再拼一个就重叠了,所以不能密铺。
⑤正八边形每个内角是135°,两个内角拼在一起270°,三个内角拼在一起有重叠了,所以不能密铺。
小结:通过观察,你觉得一个图形能否单独密铺和什么有关系?(一个拼接点处的所有角的和为360°。)
【设计意图】通过启发学生质疑,鼓励学生深入思考问题,通过多媒体动态演示,帮助学生初步建立正多边形密铺的基本条件,一个拼接点处的所有角的和为360°。
5.联系生活,拓展延伸
(1)其实我们生活中,很多精美的图案都是密铺得来的,想一想生活中还有哪些密铺的现象?
(2)图形的密铺在生活中应用广泛,人们也在用密铺完成着更奇妙的创造。(课件出示:棋盘、蜂巢、墙和门、水立方等图片)
? ?? ???
仔细观察水立方每个面上的图形,你有什么发现?
预设1:图形是不规则的。
预设2:不规则的平面图形也能密铺。
6.二次合作,深度密铺
(1)启发猜测? 布置任务
下面这些图形都不是正多边形,它们能单独密铺吗?
???
课件出示小组活动要求:
①观察猜测:把观察猜测记录在《学习报告单》上。
②验证交流:每人选择一种图形进行验证,并在组内进行交流。
③记录结果:把操作验证的结果记录在《学习报告单》上。
④想一想:你们有什么新发现?
(2)小组合作? 实践探究
师:将上一次操作的图形放回操作盒1,打开操作盒2,限时3分钟,开始。(教师操作计时器)
(3)成果展示? 汇报交流
师:请一个小组来展示,并回应全班:这些三角形和四边形都能单独密铺。举起每个人的密铺作品大家看一看。
(4)设疑激思? 引发思考
评:同学合作高效、概括能力强、动手能力强。各个小组真是太智慧了,发现任意的三角形和四边形都能单独密铺。(进行第三次小组积分评价。)这是为什么呢?
预设1:两个完全一样的三角形能拼摆成一个平行四边形(或长方形),平行四边形(或长方形)能密铺,所以任意三角形都能密铺。
预设2:两个完全一样的梯形能拼摆成一个平行四边形,平行四边形能密铺,所以任意三角形都能密铺。
预设3:四边形的内角和是360?,围绕拼接点能拼成360?,所以任意四边形都能单独密铺。
预设4:三角形内角和是180?,围绕拼接点总能拼成360?,所以任意三角形都能单独密铺。
配合学生发言,教师随机展示交互式课件。
评:把新图形转化成已知图形、推理能力、善学习善思考。
【设计意图】一般三角形和四边形能否密铺,对于学生来说不容易进行想像,再次为学生提供拼摆操作的机会,学生通过动手操作和联系旧知,为密铺的研究进行了拓展与延伸,加深了对图形特征的认识,同时沟通了新旧知识之间的联系,发展了学生的逻辑思维能力。
6.冥想总结,加深理解
闭上眼睛,我们一起回顾一下刚才的研究过程,我们通过观察猜测、操作验证、最后得出结论,发现长方形、正方形、任意的三角形、任意的四边形、正六边形都能单独密铺,正五边形、正八边形和圆不能单独密铺。
【设计意图】在探讨单一平面图形的密铺过程中,教师从正多边形拓展到普通三角形和四边形的密铺,紧密联系图形的特征,结合图形的平移、旋转等变换方法,激发学生努力发挥想象力,在猜测、验证、讨论中加深对密铺条件的理解,发展了学生的推理、归纳、概括能力。
(二)两种平面图形的密铺(5’)
1.观察想像,诱发创新
正五边形、正八边形和圆不能单独密铺,但如果与其他图形结合起来,能不能实现密铺呢?
如果用圆、正五边形、正八边形与另外一种平面图形组合进行密铺,你会分别选择下面哪个图形与他们搭配?
???????
【设计意图】引导学生观察、想像,选择两种平面图形搭配进行密铺,有效地培养学生的空间想像力。
活动4【讲授】三、欣赏作品,渗透文化(2’)
提到密铺,不得不向大家介绍一个人——荷兰著名画家埃舍尔。他的作品令人赏心悦目,趣味无穷。人们称埃舍尔是“图形的艺术家”,是数学与艺术完美结合的典范。
? ?? ?? ??
【设计意图】通过初步了解密铺的历史,欣赏埃舍尔的优秀作品,感受数学与艺术的完美结合,图形密铺的神奇和美妙,同时使学生感受到艺术家的伟大创造力,为学生梳理刻苦钻研的意识,促进学生用数学的眼光观察生活、发现生活、分析生活、解决生活问题的意识和习惯。
活动5【作业】四、布置作业,拓展延伸(1’)
很美吧?你们想不想也来设计一幅作品呢?(课件出示:动手试一试和小小设计师要求)
1.动手试一试:用画一画或摆一摆的方法,继续探索下面的图形能不能单独密铺。
????????????
2.小小设计师:发挥你的想象,用至少两种不同的图形进行密铺,在方格纸上设计出美丽的图案,并涂上颜色。或者用彩色卡纸剪出两种及以上的不同图形,粘贴成一幅美丽的密铺作品。
