江西省赣州一中2019-2020学年度第二学期高二年级线上教学质量评估试题数学试题(文)(word版含答案)
文档属性
| 名称 | 江西省赣州一中2019-2020学年度第二学期高二年级线上教学质量评估试题数学试题(文)(word版含答案) | 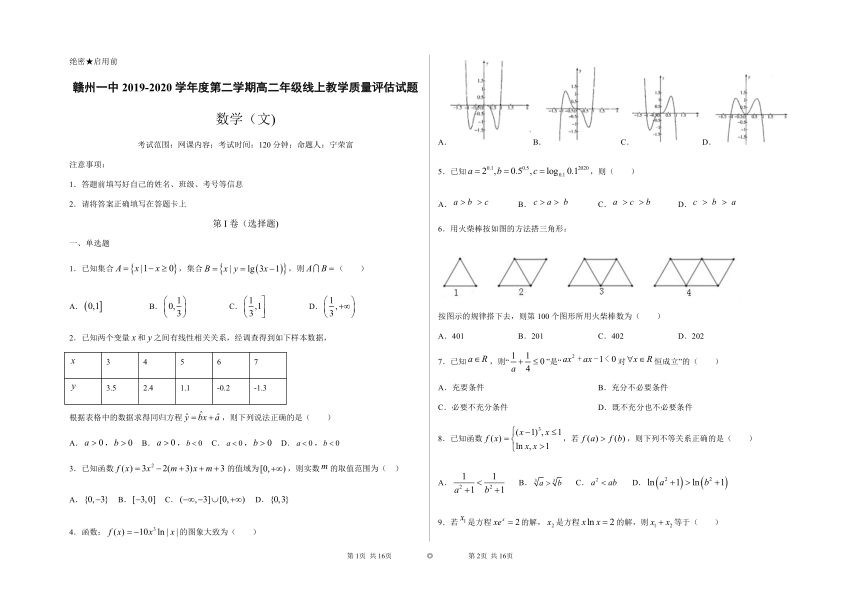 | |
| 格式 | zip | ||
| 文件大小 | 684.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 07:16:59 | ||
图片预览




文档简介
绝密★启用前
赣州一中2019-2020学年度第二学期高二年级线上教学质量评估试题
数学(文)
考试范围:网课内容;考试时间:120分钟;命题人:宁荣富
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.已知集合,集合,则( )
A. B. C. D.
2.已知两个变量和之间有线性相关关系,经调查得到如下样本数据,
3 4 5 6 7
3.5 2.4 1.1 -0.2 -1.3
根据表格中的数据求得同归方程,则下列说法正确的是( )
A., B., C., D.,
3.已知函数的值域为,则实数的取值范围为( )
A. B. C. D.
4.函数:的图象大致为( )
A.B.C.D.
5.已知,则( )
A. B. C. D.
6.用火柴棒按如图的方法搭三角形:
按图示的规律搭下去,则第100个图形所用火柴棒数为( )
A.401 B.201 C.402 D.202
7.已知,则“”是“对恒成立”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
8.已知函数,若,则下列不等关系正确的是( )
A. B. C. D.
9.若是方程的解,是方程的解,则等于( )
A. B. C. D.
10.将一个底面半径为,高为的圆锥形工件切割成一个圆柱体,能切割出的圆柱最大体积为( )
A. B. C. D.
11.已知三个正实数、、满足,给出以下几个结论:①;②;③;④.则正确的结论个数为( )
A.1 B.2 C.3 D.4
12.已知函数是定义域为的偶函数,且满足,当时,,则函数在区间上零点的个数为( )
A.9 B.10 C.18 D.20
第II卷(非选择题)
二、填空题
13.曲线在点处的切线方程为__________.
14.若复数满足(为虚数单位,表示复数的共轭复数),则的虚部为______.
15.已知为椭圆上的任意一点,则的最大值为________.
16.已知函数,若恒成立,则实数的取值范围为___________.
三、解答题
17. 若,,(为实数),为虚数单位.
(1)求复数;
(2)求的取值范围.
18.已知,p:;q:不等式对任意实数x恒成立.
(1)若q为真命题,求实数m的取值范围;
(2)如果“”为真命题,且“”为假命题,求实数m的取值范围.
19.已知函数.
(1)在如图所示的坐标系中作出的图象,并结合图象写出不等式的解集;
(2)若函数的图象恒在轴的上方,求实数的取值范围.
20.在平面直角坐标系中,直线的参数方程为(为参数),曲线的参数方程为(为参数),曲线与轴交于两点.以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(1)求直线的普通方程及曲线的极坐标方程;
(2)若直线与曲线在第一象限交于点,且线段的中点为,点在曲线上,求的最小值.
21.为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,如有些对象对普查有误解,配合不够主动;参与普查工作的技术人员对全新的操作平台运用还不够熟练等,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位, 150 家个体经营户,普查情况如下表所示:
普查对象类别 顺利 不顺利 合计
企事业单位 40 50
个体经营户 50 150
合计
(1) 写出选择 5 个国家综合试点地区采用的抽样方法;
(2) 补全上述列联表(在答题卡填写),并根据列联表判断是否有 90%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3) 根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:
22.已知函数,设的导函数为.
(1)求证:;
(2)设的极大值点为,求证:.(其中)
赣州一中2019-2020学年度第二学期高二年级线上教学质量评估试题
数学答案(文)
一、单选题
1.C 2.B 3.A 4.C 5.B 6.B 7.D 8.B 9.B 10.C 11.B 12.B
二填空题
. 14.-1 15.9
16.
解析:定义域为,
构造函数,
,
由于,令解得,
所以时,,递减,
时,,递增,
所以在上的极小值也即是最小值为
,
所以,
也即当时,.
所以由,
得,可得,
其中.
令,.可得函数的增区间为.减区间为,可得.
即.
故实数的取值范围为
三、解答题
17.若,,(为实数),为虚数单位.
(1)求复数;
(2)求的取值范围.
17.(1);(2).
(1)设,则,,
即,所以,解得,;
(2)
,
,,
,故的取值范围是.
18.已知,p:;q:不等式对任意实数x恒成立.
(1)若q为真命题,求实数m的取值范围;
(2)如果“”为真命题,且“”为假命题,求实数m的取值范围.
【答案】(1)(2)
(1)由“不等式对任意实数x恒成立”为真得,解得,故实数m的取值范围为.
(2)由“”为真得m的取值范围为,
由“”为真,且“”为假知p,q一真假,
当p真q假时,有,此时m无解;
当p假q真时,有,解得或;
综上所述,m的取值范围为.
19.已知函数.
(1)在如图所示的坐标系中作出的图象,并结合图象写出不等式的解集;
(2)若函数的图象恒在轴的上方,求实数的取值范围.
【答案】(1)见解析,(2)
【详解】
(1)
结合图象可知,当时,,;
当时,,解得;
当时,成立.
综上,不等式的解集为.
(2)若函数的图象恒在轴的上方,则恒成立,
即恒成立,只需.
由(1)中图象可知.
所以,解得.
20.在平面直角坐标系中,直线的参数方程为(为参数),曲线的参数方程为(为参数),曲线与轴交于两点.以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(1)求直线的普通方程及曲线的极坐标方程;
(2)若直线与曲线在第一象限交于点,且线段的中点为,点在曲线上,求的最小值.
【答案】(1); (2)
【详解】
(1)由可得,即,
所以直线的普通方程为.
由可得,即,
将,代入上式,可得,即,
所以曲线的极坐标方程为.
(2)由,可得或,
因为点位于第一象限,所以,
由(1)可得,因为线段的中点为,所以,
由(1)可知曲线表示圆,其圆心为,半径,
所以,
因为点在曲线上,所以.
21.为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,如有些对象对普查有误解,配合不够主动;参与普查工作的技术人员对全新的操作平台运用还不够熟练等,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位, 150 家个体经营户,普查情况如下表所示:
普查对象类别 顺利 不顺利 合计
企事业单位 40 50
个体经营户 50 150
合计
(1) 写出选择 5 个国家综合试点地区采用的抽样方法;
(2) 补全上述列联表(在答题卡填写),并根据列联表判断是否有 90%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3) 根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
【详解】
(1) 分层抽样
(2) 完成列联表
普查对象类别 顺利 不顺利 合计
企事业单位 40 10 50
个体经营户 100 50 150
合计 140 60 200
将列联表中的数据代入公式计算得
,
所以有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”.
(3)(意思相近即可得分)
建议:加大宣传力度,消除误解因素,尤其要做好个体经营户的思想工作.
22.已知函数,设的导函数为.
(1)求证:;
(2)设的极大值点为,求证:.(其中)
【答案】(1)见解析(2)见解析
解:(1)由已知的导函数为.
要证,只需要证明.
设,则.
故在递减,在递增,
故.
(2)证明:因为,
所以.
令,则
可知,当时,单调递减,当,时,单调递增.
又,, ,所以在有唯一零点,
在,有唯一零点1.
且当,,当,,,所以是的唯一的极大值
点,故,,
所以
因为,显然
故.
【点睛】
本题考查利用导数研究函数的单调性,利用导数研究函数的极值,属于中档题.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
赣州一中2019-2020学年度第二学期高二年级线上教学质量评估试题
数学(文)
考试范围:网课内容;考试时间:120分钟;命题人:宁荣富
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.已知集合,集合,则( )
A. B. C. D.
2.已知两个变量和之间有线性相关关系,经调查得到如下样本数据,
3 4 5 6 7
3.5 2.4 1.1 -0.2 -1.3
根据表格中的数据求得同归方程,则下列说法正确的是( )
A., B., C., D.,
3.已知函数的值域为,则实数的取值范围为( )
A. B. C. D.
4.函数:的图象大致为( )
A.B.C.D.
5.已知,则( )
A. B. C. D.
6.用火柴棒按如图的方法搭三角形:
按图示的规律搭下去,则第100个图形所用火柴棒数为( )
A.401 B.201 C.402 D.202
7.已知,则“”是“对恒成立”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
8.已知函数,若,则下列不等关系正确的是( )
A. B. C. D.
9.若是方程的解,是方程的解,则等于( )
A. B. C. D.
10.将一个底面半径为,高为的圆锥形工件切割成一个圆柱体,能切割出的圆柱最大体积为( )
A. B. C. D.
11.已知三个正实数、、满足,给出以下几个结论:①;②;③;④.则正确的结论个数为( )
A.1 B.2 C.3 D.4
12.已知函数是定义域为的偶函数,且满足,当时,,则函数在区间上零点的个数为( )
A.9 B.10 C.18 D.20
第II卷(非选择题)
二、填空题
13.曲线在点处的切线方程为__________.
14.若复数满足(为虚数单位,表示复数的共轭复数),则的虚部为______.
15.已知为椭圆上的任意一点,则的最大值为________.
16.已知函数,若恒成立,则实数的取值范围为___________.
三、解答题
17. 若,,(为实数),为虚数单位.
(1)求复数;
(2)求的取值范围.
18.已知,p:;q:不等式对任意实数x恒成立.
(1)若q为真命题,求实数m的取值范围;
(2)如果“”为真命题,且“”为假命题,求实数m的取值范围.
19.已知函数.
(1)在如图所示的坐标系中作出的图象,并结合图象写出不等式的解集;
(2)若函数的图象恒在轴的上方,求实数的取值范围.
20.在平面直角坐标系中,直线的参数方程为(为参数),曲线的参数方程为(为参数),曲线与轴交于两点.以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(1)求直线的普通方程及曲线的极坐标方程;
(2)若直线与曲线在第一象限交于点,且线段的中点为,点在曲线上,求的最小值.
21.为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,如有些对象对普查有误解,配合不够主动;参与普查工作的技术人员对全新的操作平台运用还不够熟练等,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位, 150 家个体经营户,普查情况如下表所示:
普查对象类别 顺利 不顺利 合计
企事业单位 40 50
个体经营户 50 150
合计
(1) 写出选择 5 个国家综合试点地区采用的抽样方法;
(2) 补全上述列联表(在答题卡填写),并根据列联表判断是否有 90%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3) 根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:
22.已知函数,设的导函数为.
(1)求证:;
(2)设的极大值点为,求证:.(其中)
赣州一中2019-2020学年度第二学期高二年级线上教学质量评估试题
数学答案(文)
一、单选题
1.C 2.B 3.A 4.C 5.B 6.B 7.D 8.B 9.B 10.C 11.B 12.B
二填空题
. 14.-1 15.9
16.
解析:定义域为,
构造函数,
,
由于,令解得,
所以时,,递减,
时,,递增,
所以在上的极小值也即是最小值为
,
所以,
也即当时,.
所以由,
得,可得,
其中.
令,.可得函数的增区间为.减区间为,可得.
即.
故实数的取值范围为
三、解答题
17.若,,(为实数),为虚数单位.
(1)求复数;
(2)求的取值范围.
17.(1);(2).
(1)设,则,,
即,所以,解得,;
(2)
,
,,
,故的取值范围是.
18.已知,p:;q:不等式对任意实数x恒成立.
(1)若q为真命题,求实数m的取值范围;
(2)如果“”为真命题,且“”为假命题,求实数m的取值范围.
【答案】(1)(2)
(1)由“不等式对任意实数x恒成立”为真得,解得,故实数m的取值范围为.
(2)由“”为真得m的取值范围为,
由“”为真,且“”为假知p,q一真假,
当p真q假时,有,此时m无解;
当p假q真时,有,解得或;
综上所述,m的取值范围为.
19.已知函数.
(1)在如图所示的坐标系中作出的图象,并结合图象写出不等式的解集;
(2)若函数的图象恒在轴的上方,求实数的取值范围.
【答案】(1)见解析,(2)
【详解】
(1)
结合图象可知,当时,,;
当时,,解得;
当时,成立.
综上,不等式的解集为.
(2)若函数的图象恒在轴的上方,则恒成立,
即恒成立,只需.
由(1)中图象可知.
所以,解得.
20.在平面直角坐标系中,直线的参数方程为(为参数),曲线的参数方程为(为参数),曲线与轴交于两点.以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(1)求直线的普通方程及曲线的极坐标方程;
(2)若直线与曲线在第一象限交于点,且线段的中点为,点在曲线上,求的最小值.
【答案】(1); (2)
【详解】
(1)由可得,即,
所以直线的普通方程为.
由可得,即,
将,代入上式,可得,即,
所以曲线的极坐标方程为.
(2)由,可得或,
因为点位于第一象限,所以,
由(1)可得,因为线段的中点为,所以,
由(1)可知曲线表示圆,其圆心为,半径,
所以,
因为点在曲线上,所以.
21.为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,如有些对象对普查有误解,配合不够主动;参与普查工作的技术人员对全新的操作平台运用还不够熟练等,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位, 150 家个体经营户,普查情况如下表所示:
普查对象类别 顺利 不顺利 合计
企事业单位 40 50
个体经营户 50 150
合计
(1) 写出选择 5 个国家综合试点地区采用的抽样方法;
(2) 补全上述列联表(在答题卡填写),并根据列联表判断是否有 90%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3) 根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
【详解】
(1) 分层抽样
(2) 完成列联表
普查对象类别 顺利 不顺利 合计
企事业单位 40 10 50
个体经营户 100 50 150
合计 140 60 200
将列联表中的数据代入公式计算得
,
所以有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”.
(3)(意思相近即可得分)
建议:加大宣传力度,消除误解因素,尤其要做好个体经营户的思想工作.
22.已知函数,设的导函数为.
(1)求证:;
(2)设的极大值点为,求证:.(其中)
【答案】(1)见解析(2)见解析
解:(1)由已知的导函数为.
要证,只需要证明.
设,则.
故在递减,在递增,
故.
(2)证明:因为,
所以.
令,则
可知,当时,单调递减,当,时,单调递增.
又,, ,所以在有唯一零点,
在,有唯一零点1.
且当,,当,,,所以是的唯一的极大值
点,故,,
所以
因为,显然
故.
【点睛】
本题考查利用导数研究函数的单调性,利用导数研究函数的极值,属于中档题.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
同课章节目录
