人教A版高中数学选修1-1 第三章3.1.1 变化率问题教学课件 (共21张PPT)
文档属性
| 名称 | 人教A版高中数学选修1-1 第三章3.1.1 变化率问题教学课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 11:26:45 | ||
图片预览





文档简介
(共21张PPT)
§3.1 变化率与导数
牛顿
微积分的主要创始人
牛顿:英国著名的物理学家、数学家、天文学家、哲学家。牛顿创立了经典力学体系,发现了运动三定律和万有引力定律。在数学领域中,他建立了二项式定理,并创立了微积分理论。
莱布尼兹(茨):德意志哲学家、数学家。莱布尼茨在数学史和哲学史上都占有重要地位。在数学上,他和牛顿先后独立发明了微积分。有人认为,莱布尼茨最大的贡献不是发明微积分,而是发明了微积分中使用的数学符号,因为牛顿使用的符号被普遍认为比莱布尼茨的差。
微积分的主要创始人
莱布尼兹(茨)
我们都吹过气球,回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.
从数学角度,如何描述这种现象呢?
气球的体积V(单位:L)与半径r(单
位:dm)之间的函数关系是:
用V 表示r得:
问题一:气球膨胀率
第一次
第二次
0.62dm
0.16dm
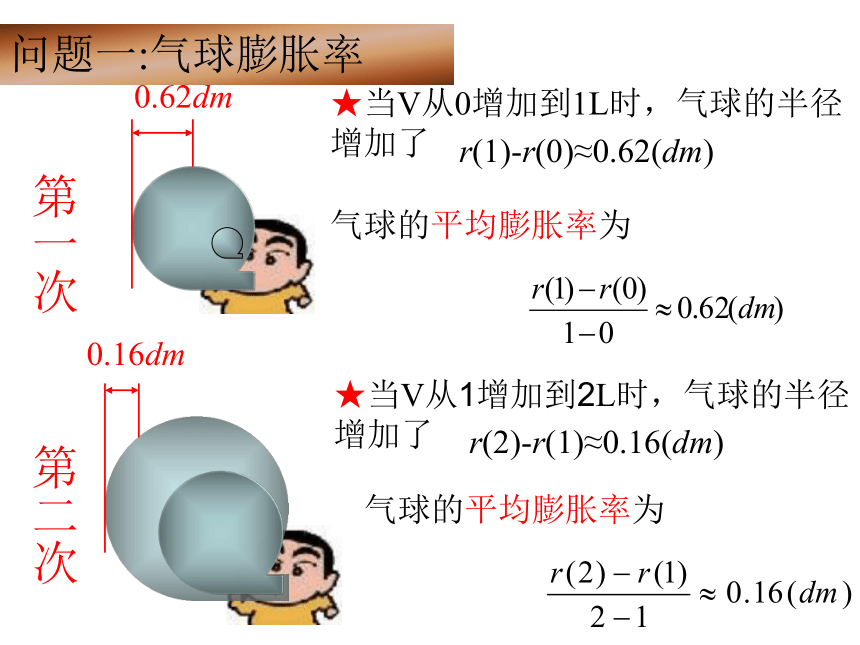
问题一:气球膨胀率
★当V从0增加到1L时,气球的半径增加了
r(1)-r(0)≈0.62(dm)
气球的平均膨胀率为
★当V从1增加到2L时,气球的半径增加了
r(2)-r(1)≈0.16(dm)
气球的平均膨胀率为
当气球的空气容量从V1增加到V2时,
气球的平均膨胀率是多少?
思考
问题一:气球膨胀率
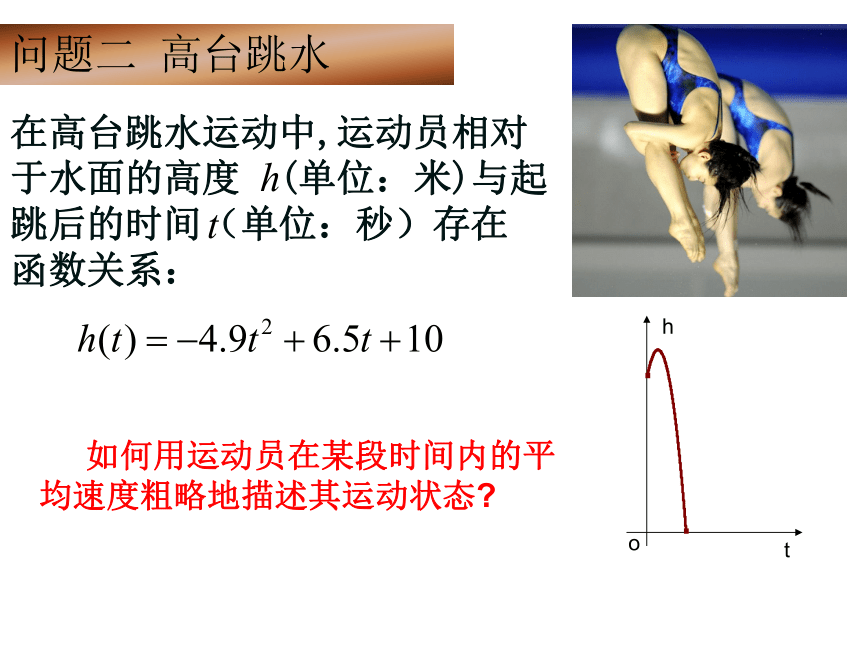
问题二 高台跳水
在高台跳水运动中,运动员相对
于水面的高度 (单位:米)与起
跳后的时间(单位:秒)存在
函数关系:
如何用运动员在某段时间内的平均速度粗略地描述其运动状态?
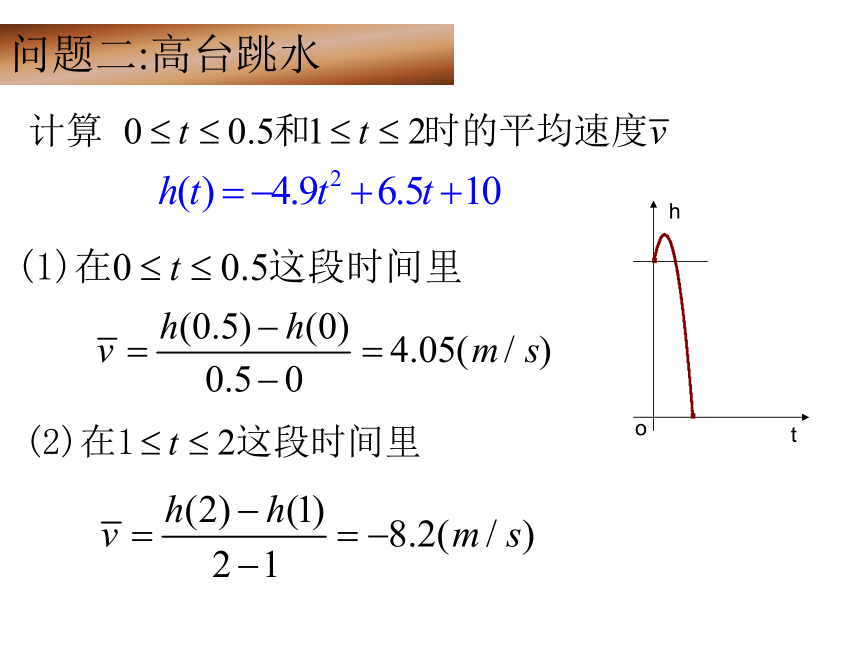
问题二:高台跳水
思考
问题二:高台跳水
气球的平均膨胀率和运动员在某段时间的平均速度是特殊的情况,我们把这一思路延伸到函数上,如果上述问题的函数关系用 表示,那么问题中变化率可用式子表示,
探究活动
观察函数 的图象
平均变化率
表示什么?
O
A
B
直线AB的斜率
思考
平均变化率的几何意义?P74
平均变化率表示函数图像上两点连线的斜率,即割线的斜率。
2.求函数y=5x2+6在区间[2,2+△x]内的平均变化率。
解:
随堂练习
1.函数 在区间 上的平均变化率( )
A. 4 B. 2 C. D.
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
平均速度只是粗略地描述这段时间内运动员运动的快慢,不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态。
(1)运动员在这段
时间里是静止的吗?
考察t=2附近的平均速度
通过列表看出平均速度的变化趋势?:
瞬时速度
我们用
因此,运动员在某一时刻t0的瞬时速度为:
思考
导数的定义:
它说明在第2(h)附近,原油温度大约以3 0C/H的速度下降;在第6(h)附近,原油温度大约以5 0C/H的速度上升。
关键是求出:
例1将原油精练为汽油、柴油、塑胶等各种不同产品,需要对原由进行冷却和加热。如果第 (h)时,原油的温度(单位:0C)为 .计算第2(h)和第6(h)时,原油温度的瞬时变化率,并说明它们的意义。
1.通过本节课的学习你有哪些收获?
课堂小结
平均变化率、瞬时变化率(即导数)
体会了函数思想、逼近思想方法、概念形成
过程中的抽象概括
课后作业
1.必做题1~3,选做题4~5
2.上网查阅微积分创始人的有关资料
§3.1 变化率与导数
牛顿
微积分的主要创始人
牛顿:英国著名的物理学家、数学家、天文学家、哲学家。牛顿创立了经典力学体系,发现了运动三定律和万有引力定律。在数学领域中,他建立了二项式定理,并创立了微积分理论。
莱布尼兹(茨):德意志哲学家、数学家。莱布尼茨在数学史和哲学史上都占有重要地位。在数学上,他和牛顿先后独立发明了微积分。有人认为,莱布尼茨最大的贡献不是发明微积分,而是发明了微积分中使用的数学符号,因为牛顿使用的符号被普遍认为比莱布尼茨的差。
微积分的主要创始人
莱布尼兹(茨)
我们都吹过气球,回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.
从数学角度,如何描述这种现象呢?
气球的体积V(单位:L)与半径r(单
位:dm)之间的函数关系是:
用V 表示r得:
问题一:气球膨胀率
第一次
第二次
0.62dm
0.16dm
问题一:气球膨胀率
★当V从0增加到1L时,气球的半径增加了
r(1)-r(0)≈0.62(dm)
气球的平均膨胀率为
★当V从1增加到2L时,气球的半径增加了
r(2)-r(1)≈0.16(dm)
气球的平均膨胀率为
当气球的空气容量从V1增加到V2时,
气球的平均膨胀率是多少?
思考
问题一:气球膨胀率
问题二 高台跳水
在高台跳水运动中,运动员相对
于水面的高度 (单位:米)与起
跳后的时间(单位:秒)存在
函数关系:
如何用运动员在某段时间内的平均速度粗略地描述其运动状态?
问题二:高台跳水
思考
问题二:高台跳水
气球的平均膨胀率和运动员在某段时间的平均速度是特殊的情况,我们把这一思路延伸到函数上,如果上述问题的函数关系用 表示,那么问题中变化率可用式子表示,
探究活动
观察函数 的图象
平均变化率
表示什么?
O
A
B
直线AB的斜率
思考
平均变化率的几何意义?P74
平均变化率表示函数图像上两点连线的斜率,即割线的斜率。
2.求函数y=5x2+6在区间[2,2+△x]内的平均变化率。
解:
随堂练习
1.函数 在区间 上的平均变化率( )
A. 4 B. 2 C. D.
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
平均速度只是粗略地描述这段时间内运动员运动的快慢,不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态。
(1)运动员在这段
时间里是静止的吗?
考察t=2附近的平均速度
通过列表看出平均速度的变化趋势?:
瞬时速度
我们用
因此,运动员在某一时刻t0的瞬时速度为:
思考
导数的定义:
它说明在第2(h)附近,原油温度大约以3 0C/H的速度下降;在第6(h)附近,原油温度大约以5 0C/H的速度上升。
关键是求出:
例1将原油精练为汽油、柴油、塑胶等各种不同产品,需要对原由进行冷却和加热。如果第 (h)时,原油的温度(单位:0C)为 .计算第2(h)和第6(h)时,原油温度的瞬时变化率,并说明它们的意义。
1.通过本节课的学习你有哪些收获?
课堂小结
平均变化率、瞬时变化率(即导数)
体会了函数思想、逼近思想方法、概念形成
过程中的抽象概括
课后作业
1.必做题1~3,选做题4~5
2.上网查阅微积分创始人的有关资料
